���啨��'05�N�O��[2]
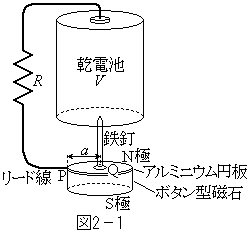 �@�}2�|1�̂悤�ɁA�{�^���^���Ɣ����A���~�j�E���̉~��\�荇�킹�����̂��A���̎��͂��g���ēS�B����Ċ��d�r�̓S�����d�ɂɂ邷�B���d�r�̐��ɂ��烊�[�h�����̂��A��R����ă��[�h���̑��[P���A���~�j�E���~�̉~����̓_�ɐG�ꂳ����ƁA�A���~�j�E���~�ƃ{�^���^���͉�]���n�߂��B���̌�A���[�h���ƃA���~�j�E���~�����ׂ�Ȃ���ڐG����悤�Ƀ��[�h����ێ�����ƁA�~�Ǝ��͉�]���������B�{�^���^���́A�}2�|1�̂悤�ɏ�ʂ�N�ɁA���ʂ�S�ɂŁA�d�C��ʂ��Ȃ��B�A���~�j�E���~�̔��a��a[m]�A���d�r�̋N�d�͂�V[V]�A��R�̒�R�l��R[Ω]�A�A���~�j�E���~���т��������xB[T]�͉~�ʓ��ň�l�Ƃ��āA�ȉ��̖�ɓ�����B�������A���[�h���ƃA���~�j�E���~�̊Ԃ̖��C�A�S�B�Ɠd�r�̊Ԃ̖��C�͖������Ă悢�B�܂��A�A���~�j�E���~�ƓS�B�̊Ԃ̖��C�͏\���傫���A�����͈�̂ɂȂ��ĉ�]������̂Ƃ���B
�@�}2�|1�̂悤�ɁA�{�^���^���Ɣ����A���~�j�E���̉~��\�荇�킹�����̂��A���̎��͂��g���ēS�B����Ċ��d�r�̓S�����d�ɂɂ邷�B���d�r�̐��ɂ��烊�[�h�����̂��A��R����ă��[�h���̑��[P���A���~�j�E���~�̉~����̓_�ɐG�ꂳ����ƁA�A���~�j�E���~�ƃ{�^���^���͉�]���n�߂��B���̌�A���[�h���ƃA���~�j�E���~�����ׂ�Ȃ���ڐG����悤�Ƀ��[�h����ێ�����ƁA�~�Ǝ��͉�]���������B�{�^���^���́A�}2�|1�̂悤�ɏ�ʂ�N�ɁA���ʂ�S�ɂŁA�d�C��ʂ��Ȃ��B�A���~�j�E���~�̔��a��a[m]�A���d�r�̋N�d�͂�V[V]�A��R�̒�R�l��R[Ω]�A�A���~�j�E���~���т��������xB[T]�͉~�ʓ��ň�l�Ƃ��āA�ȉ��̖�ɓ�����B�������A���[�h���ƃA���~�j�E���~�̊Ԃ̖��C�A�S�B�Ɠd�r�̊Ԃ̖��C�͖������Ă悢�B�܂��A�A���~�j�E���~�ƓS�B�̊Ԃ̖��C�͏\���傫���A�����͈�̂ɂȂ��ĉ�]������̂Ƃ���B
�T�@�A���~�j�E���~�ƃ{�^���^������]����������A���R��t���ē�����B���}���g���Ă��悢�B�������A�A���~�j�E���~�𗬂��d���́A�S�B�Ƃ̐ڍ��_Q�Ɠ_P�̊ԂړI�ɗ����ƍl���Ă悢�B
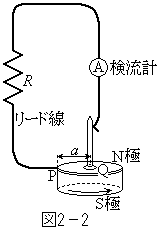 �U�@�}2�|2�̂悤�ɁA���d�r�̂����Ɍ����v��u���B�A���~�j�E���~�ƃ{�^���^����}2�|2�̖������ɗ͂������ĉ�]������ƁA�����v�ɓd�������ꂽ�B�d���̗��������𗝗R��t���ē�����B
�U�@�}2�|2�̂悤�ɁA���d�r�̂����Ɍ����v��u���B�A���~�j�E���~�ƃ{�^���^����}2�|2�̖������ɗ͂������ĉ�]������ƁA�����v�ɓd�������ꂽ�B�d���̗��������𗝗R��t���ē�����B
�V�@�U�Ő����Ă����N�d��E[V]�̑傫���́A�{�^���^���̉�]�̊p���x��ω[rad/s]�̂Ƃ��A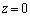 �ƕ\���邱�Ƃ������A�W��b�����߂�B�������A�B�͏\���ׂ��Ƃ��Ă悢�B
�ƕ\���邱�Ƃ������A�W��b�����߂�B�������A�B�͏\���ׂ��Ƃ��Ă悢�B
�W�@�}2�|1�ɂ������A�[�����Ԃ��o�ƃA���~�j�E���~�ƃ{�^���^���̊p���x�͂�����l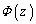 [rad/s]�ɂȂ�B
[rad/s]�ɂȂ�B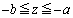 ��V�CB�Cb��p���ĕ\���B
��V�CB�Cb��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���T�@�t���~���O����̖@���ōl���܂��BP��Q�̕������d��������܂��B���ꂪ���蒆�w�̌����B�A���~�j�E���~��ʂ��āA�{�^���^������B�̕��Ɍ����������E���ł���̂ŁA�B�̑�����A���~�j�E���~�����āA��O���������E�ł��B���ꂪ����l�����w�̌����B���̂Ƃ��A����̐e�w�́A�B�̑����猩�Ĕ����v���̕����������܂��B���ꂪ�A�d���̎��d�����̌����B�]���āA��]�����́A�B�̑����猩�āA�����v���ł��B �ォ�猩�āA�����v��� ......[��]
�U�@�����v�̓B����C�C�t����D�Ƃ��܂��B
�t���~���O�E��̖@���ōl����Ȃ�A�B�̑����猩�āA����PQ�́A���E�����v�����ړ����܂��B���ꂪ�E��e�w�̌����B�B�̑����猩�āA���E�͎�O�����ŁA���ꂪ�E��l�����w�̌����B���̂Ƃ��E�蒆�w��Q��P�������܂��B�]���āA�����v��D��C�̕������d��������܂��B
�����v��B�Ƌt������B�̕��Ɍ������ė���� ......[��]�����c�̖@���ōl����̂Ȃ�A�B�̑����猩�āA����PQ�͔����v���ɉ�]����̂ŁA������W����������N�d���������܂��B�܂����PQ�����v���̕����ɗ͂���悤���N�d�����������܂��B�T���AP��Q�������d���ł͔����v���̗͂Ȃ̂ŁA�����ł́AQ��P�̌������d��������܂��B
����PQ������d��q�̎����[�����c�����l���邱�Ƃ��ł��܂��B�B�̑����猩�āAq�͔����v���Ɉړ�����̂ŁA�����v�����d���������ƍl���܂��B���ꂪ���蒆�w�̌����B���E�͓B���猩�Ď�O�����B���ꂪ����l�����w�̌����ł��B���̂Ƃ��A����e�w��Q��P�̕����������܂��B�t���~���O����̖@�����Aq�̎����[�����c���̌�����Q��P�ł��B���ꂪ�N�d���̌����ł���A�d���̌����ł��B
�V�@��������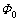 �̊Ԃɐ���PQ�̉�]�����p��
�̊Ԃɐ���PQ�̉�]�����p��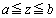 �ł��B���aa�C���p
�ł��B���aa�C���p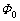 �̐�`���ʐ��́A
�̐�`���ʐ��́A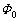 �ł��B�����ʐ����т����������́A
�ł��B�����ʐ����т����������́A �� 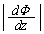 ......[��]
......[��]
�W�@��]���p���x�����l�ɂȂ�Ƃ������Ƃ́A�A���~�j�E���~�̉~�����ڐ������ɂ͓͗͂����Ȃ��Ƃ������Ƃ��Ӗ����܂�(�����~�^���Q��)�B����PQ�Ԃ��d���������Ɛڐ����������������Ă��܂��̂ŁA����PQ�Ԃɂ��d��������Ă��Ȃ����Ƃ��킩��܂��B ���d�r���ڑ�����Ă���̂��d��������Ȃ��A�Ƃ������Ƃ́A���d�r�̋N�d�͂�ł������N�d��������PQ�Ԃɔ������Ă���Ƃ������Ƃł��B�V���A�A���~�j�E���~���B�����猩�Ĕ����v�����p���x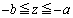 �ʼn�]����Ƃ��AQ��P�̌������d���𗬂��N�d��
�ʼn�]����Ƃ��AQ��P�̌������d���𗬂��N�d��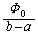 ���������܂��B�]���āA
���������܂��B�]���āA �� 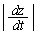 [rad/s] ......[��]
[rad/s] ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B