東京大学2006年前期物理入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
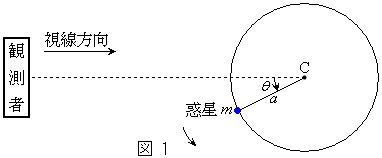
[1] 太陽系以外で、恒星の周りを公転する惑星が初めて発見されたのは1995年である。以来、すでに150個以上の太陽系外惑星が発見されている。この太陽系外惑星の検出原理は、質量Mの恒星と質量mの惑星( )が、互いの万有引力だけによってそれぞれ運動している場合を考えれば理解できる。この場合、惑星は一般には楕円軌道上を運動することが知られている。しかしここでは図1に示すように、惑星がある定点Cを中心とした半径aの円周上を等速円運動しているとする(だたし、図1には恒星を図示していないことに注意)。万有引力定数をGとし、恒星および惑星の大きさは無視する。
)が、互いの万有引力だけによってそれぞれ運動している場合を考えれば理解できる。この場合、惑星は一般には楕円軌道上を運動することが知られている。しかしここでは図1に示すように、惑星がある定点Cを中心とした半径aの円周上を等速円運動しているとする(だたし、図1には恒星を図示していないことに注意)。万有引力定数をGとし、恒星および惑星の大きさは無視する。
 Ⅰ 図1のように、惑星が反時計回りに公転しているものとする。惑星に働く向心力は恒星による万有引力であることを考えて、以下の問に答えよ。
Ⅰ 図1のように、惑星が反時計回りに公転しているものとする。惑星に働く向心力は恒星による万有引力であることを考えて、以下の問に答えよ。(1) 恒星、惑星、点Cの互いの位置関係を理由とともに述べよ。
(2) 恒星と点Cとの距離、惑星の速さv,恒星の速さVを求めよ。
(3) 惑星の公転軌道面上において、aに比べて充分に遠方にあり、点Cに対して静止している観測者を考える。図1のように惑星が角度θ [rad]の位置にあるとき、惑星の速度の視線方向成分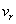 を、vとθ を用いて表せ。ただし、観測者に対して遠ざかる向きを
を、vとθ を用いて表せ。ただし、観測者に対して遠ざかる向きを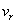 の正の向きに選ぶものとする。
の正の向きに選ぶものとする。 (4) 時刻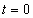 において、惑星が
において、惑星が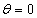 の位置にあったとする。また、惑星の公転周期をT,恒星の速度の視線方向成分を
の位置にあったとする。また、惑星の公転周期をT,恒星の速度の視線方向成分を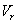 とする。
とする。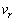 と
と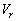 をtの関数として、その概形を
をtの関数として、その概形を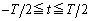 の範囲でグラフに描け。ただし、観測者に対して遠ざかる向きを
の範囲でグラフに描け。ただし、観測者に対して遠ざかる向きを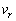 と
と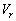 の正の向きに選ぶものとする。
の正の向きに選ぶものとする。 Ⅱ 惑星からの光は弱すぎて観測することは困難である。しかし、恒星からの光を観測することによって、惑星の存在を知ることができる。この間接的な惑星検出の方法では、運動する恒星が発する光の波長は、音源が動いた場合の音の波長と同様に、ドップラー効果によって変化することを利用する。ここでは、恒星が静止している場合には波長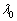 の光を発するものとして以下の問に答えよ。
の光を発するものとして以下の問に答えよ。 (1) 惑星が角度θ の位置にあるときに恒星が発する光を観測者が測定したところ、波長はλであった。光速度をcとして、波長の変化量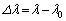 をθ の関数として求めよ。
をθ の関数として求めよ。 (2) II(1)で求めた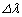 は時間変動する。
は時間変動する。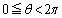 の範囲で
の範囲で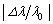 の最大値が
の最大値が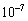 以上であれば、現在の観測技術で
以上であれば、現在の観測技術で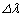 の時間変動を検出することができる。このことから、惑星の存在を知ることが可能であるためにaが満たすべき条件式を求めよ。
の時間変動を検出することができる。このことから、惑星の存在を知ることが可能であるためにaが満たすべき条件式を求めよ。 [解答へ]
[2] 真空放電による気体の発光を利用するネオンランプは、約80V以上の電圧をかけると放電し、電流が流れ点灯する。したがって、起電力が数Vの乾電池のみでネオンランプを点灯させることはできない。しかし、コイルおよびスイッチと組み合わせることにより、短時間ではあるがネオンランプを点灯させることができる。
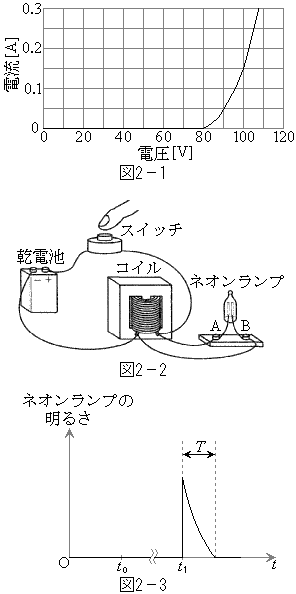 ここでは、図2-1の電圧-電流特性をもつネオンランプを起電力9.0Vの乾電池で点灯させることを考える。図2-2のように、乾電池、コイル、およびスイッチを直列につなぎ、ネオンランプをコイルと並列につなぐ。コイルの自己インダクタンスLを1.0H,コイルの抵抗を35Ω,乾電池の内部抵抗を10Ω,ネオンランプの端子Bを基準とする端子Aの電位を
ここでは、図2-1の電圧-電流特性をもつネオンランプを起電力9.0Vの乾電池で点灯させることを考える。図2-2のように、乾電池、コイル、およびスイッチを直列につなぎ、ネオンランプをコイルと並列につなぐ。コイルの自己インダクタンスLを1.0H,コイルの抵抗を35Ω,乾電池の内部抵抗を10Ω,ネオンランプの端子Bを基準とする端子Aの電位を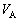 として、以下の問に答えよ。ただし、ネオンランプに流れる電流の大きさは、端子A,Bのどちらが正極であっても図2-1で与えられるとする。また、ネオンランプの電気容量、コイル以外の回路の自己インダクタンスは無視できるほど小さく、ネオンランプの明るさはネオンランプを流れる電流の大きさに比例するものとする。
として、以下の問に答えよ。ただし、ネオンランプに流れる電流の大きさは、端子A,Bのどちらが正極であっても図2-1で与えられるとする。また、ネオンランプの電気容量、コイル以外の回路の自己インダクタンスは無視できるほど小さく、ネオンランプの明るさはネオンランプを流れる電流の大きさに比例するものとする。
Ⅰ 時刻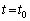 に回路のスイッチを入れたが、ネオンランプは点灯しなかった。
に回路のスイッチを入れたが、ネオンランプは点灯しなかった。 (1) スイッチを入れた直後の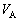 の大きさと符号を求めよ。
の大きさと符号を求めよ。 (2) スイッチを入れてしばらくすると、回路を流れる電流は一定となった。このときコイルを流れる電流の大きさ、および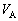 の大きさと符号を求めよ。
の大きさと符号を求めよ。 Ⅱ 回路を流れる電流が一定になった後、時刻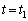 にスイッチを切った。その後、ネオンランプは図2-3のように時間Tだけ点灯した。
にスイッチを切った。その後、ネオンランプは図2-3のように時間Tだけ点灯した。 (1) 点灯が始まった直後にネオンランプを流れる電流の大きさを求めよ。
(2) 図2-1を利用して、ネオンランプの点灯が始まった直後の の大きさと符号を求めよ。
の大きさと符号を求めよ。 (3) ネオンランプの点灯が始まった直後、および点灯が終わる直前にコイルに生じている誘導起電力の大きさを、それぞれ求めよ。
Ⅲ ネオンランプの点灯時間Tのおおよその値を求めたい。計算を簡単にするため、点灯中に生じている誘導起電力の大きさは一定値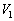 であると近似する。
であると近似する。 (1) 点灯が始まった直後にネオンランプを流れる電流の大きさを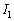 とする。点灯時間Tを
とする。点灯時間Tを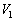 ,
,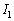 ,Lを用いて表せ。
,Lを用いて表せ。 [解答へ]
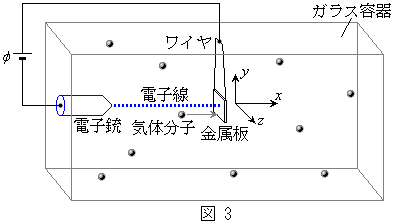 [3] 図3のように、密閉されたガラス容器(容積V)のなかに、導電性のワイヤで吊り下げた金属の板(面積S)と電子銃が取り付けられている。電子銃からは電子が初速度0で出る。その電子は電圧ϕで加速されて板に垂直に衝突する。この容器には、気体分子同士の衝突を考えなくてよいほど希薄な気体(nモル)が存在している。電子銃から出た電子は、直接板に力を与える以外に、気体分子を介して間接的に別の力を板に及ぼす。それぞれの力を求めるため、気体は理想気体の状態方程式に従うものとして、以下の問に答えよ。電子の電荷と質量をそれぞれ、
[3] 図3のように、密閉されたガラス容器(容積V)のなかに、導電性のワイヤで吊り下げた金属の板(面積S)と電子銃が取り付けられている。電子銃からは電子が初速度0で出る。その電子は電圧ϕで加速されて板に垂直に衝突する。この容器には、気体分子同士の衝突を考えなくてよいほど希薄な気体(nモル)が存在している。電子銃から出た電子は、直接板に力を与える以外に、気体分子を介して間接的に別の力を板に及ぼす。それぞれの力を求めるため、気体は理想気体の状態方程式に従うものとして、以下の問に答えよ。電子の電荷と質量をそれぞれ、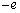 (
(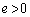 ),m,気体分子の質量をM,アボガドロ数を
),m,気体分子の質量をM,アボガドロ数を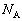 ,気体定数をRとする。また、図3のように、電子銃から板に垂直に向かう方向をx軸,それと直交する2方向をy軸,z軸とする。ただし、電子銃、板、ワイヤの体積は無視してよいものとする。
,気体定数をRとする。また、図3のように、電子銃から板に垂直に向かう方向をx軸,それと直交する2方向をy軸,z軸とする。ただし、電子銃、板、ワイヤの体積は無視してよいものとする。
Ⅰ まず、電子銃から出た電子が板に直接与える力を求めよう。ただし、すべての電子は板に垂直に衝突し、板で反射されることなく吸収されるものとする。
(1) 電子銃から出て加速された1個の電子が、板に衝突する際に板に与える力積を、ϕ,e,mを用いて表せ。
(2) 電子の流れ(電子線)によって生じる電流がIであるとき、板の表面に垂直に加わる平均の力Fを、I,ϕ,e,mを用いて表せ。
Ⅱ 次に、電子線を照射していない状態で、気体分子が板に及ぼす力を考えよう。状況を簡単化して、気体分子の1/3はx軸方向に、1/3はy軸方向に、残る1/3はz軸方向に、それぞれ同じ速さvで運動しているものとする。また、それぞれの軸方向に運動する分子の半数ずつは互いに反対向きに運動しているものとする。
(1) 単位時間に板の片側に入射する気体分子の数を、n,v,S,V,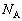 を用いて表せ。
を用いて表せ。 (2) 気体分子と板の衝突が弾性衝突のとき、気体が板に及ぼす圧力Pを、n,v,M,V,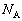 を用いて表せ。ただし、板は十分重くて動かないものとする。
を用いて表せ。ただし、板は十分重くて動かないものとする。 (3) 理想気体の状態方程式を利用して、vをM,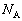 ,Rおよび気体の絶対温度Tを用いて表せ。
,Rおよび気体の絶対温度Tを用いて表せ。 (4) 実際には、気体分子と板の衝突は弾性衝突ではなく、むしろ完全非弾性衝突となることが多い。そのような気体分子は、板に衝突して板の表面に一旦吸着される。しかし、吸着された分子は再び表面から放出され、単位時間に板に入射し吸着される分子数と板から放出される分子数がつりあった状態になる。板の表面の温度が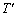 であるとき、吸着された分子はⅡ(3)のTを
であるとき、吸着された分子はⅡ(3)のTを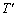 に置き換えた速さで板の表面から垂直に放出されるものとする。ここでは
に置き換えた速さで板の表面から垂直に放出されるものとする。ここでは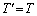 とし、入射するすべての分子が板とこのように完全非弾性衝突するとして、気体分子が吸着・放出によって板に及ぼす圧力を、n,v,M,V,
とし、入射するすべての分子が板とこのように完全非弾性衝突するとして、気体分子が吸着・放出によって板に及ぼす圧力を、n,v,M,V,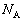 を用いて表せ。ただし、吸着による気体中の分子数の減少は無視できるものとする。また、板は動かないものとする。
を用いて表せ。ただし、吸着による気体中の分子数の減少は無視できるものとする。また、板は動かないものとする。 Ⅲ 電子照射によって板に間接的に加わる別の力を考えよう。
(1) 電子線を照射していると、入射電子の運動エネルギーによって照射面の温度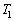 は反対側の面の温度
は反対側の面の温度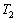 より、
より、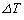 だけ上昇する。この場合、単位時間に板に入射し吸着される分子数と板から放出される分子数がつりあった状態でも、両面に気体分子が及ぼす圧力に差が生じ、板には力f が加わる。その理由と力f の向きを答よ。ただし、板に入射する気体分子の温度Tと、電子照射面の反対側の面の温度
だけ上昇する。この場合、単位時間に板に入射し吸着される分子数と板から放出される分子数がつりあった状態でも、両面に気体分子が及ぼす圧力に差が生じ、板には力f が加わる。その理由と力f の向きを答よ。ただし、板に入射する気体分子の温度Tと、電子照射面の反対側の面の温度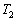 は等しく、電子線照射前と変わらないものとする。
は等しく、電子線照射前と変わらないものとする。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。