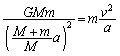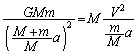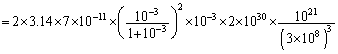東大物理'06年前期[1]
太陽系以外で、恒星の周りを公転する惑星が初めて発見されたのは1995年である。以来、すでに150個以上の太陽系外惑星が発見されている。この太陽系外惑星の検出原理は、質量Mの恒星と質量mの惑星(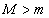 )が、互いの万有引力だけによってそれぞれ運動している場合を考えれば理解できる。この場合、惑星は一般には楕円軌道上を運動することが知られている。しかしここでは図1に示すように、惑星がある定点Cを中心とした半径aの円周上を等速円運動しているとする(だたし、図1には恒星を図示していないことに注意)。万有引力定数をGとし、恒星および惑星の大きさは無視する。
)が、互いの万有引力だけによってそれぞれ運動している場合を考えれば理解できる。この場合、惑星は一般には楕円軌道上を運動することが知られている。しかしここでは図1に示すように、惑星がある定点Cを中心とした半径aの円周上を等速円運動しているとする(だたし、図1には恒星を図示していないことに注意)。万有引力定数をGとし、恒星および惑星の大きさは無視する。
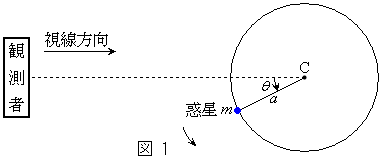 Ⅰ 図1のように、惑星が反時計回りに公転しているものとする。惑星に働く向心力は恒星による万有引力であることを考えて、以下の問に答えよ。
Ⅰ 図1のように、惑星が反時計回りに公転しているものとする。惑星に働く向心力は恒星による万有引力であることを考えて、以下の問に答えよ。(1) 恒星、惑星、点Cの互いの位置関係を理由とともに述べよ。
(2) 恒星と点Cとの距離、惑星の速さv,恒星の速さVを求めよ。
(3) 惑星の公転軌道面上において、aに比べて充分に遠方にあり、点Cに対して静止している観測者を考える。図1のように惑星が角度θ [rad]の位置にあるとき、惑星の速度の視線方向成分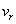 を、vとθ を用いて表せ。ただし、観測者に対して遠ざかる向きを
を、vとθ を用いて表せ。ただし、観測者に対して遠ざかる向きを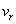 の正の向きに選ぶものとする。
の正の向きに選ぶものとする。 (4) 時刻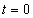 において、惑星が
において、惑星が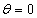 の位置にあったとする。また、惑星の公転周期をT,恒星の速度の視線方向成分を
の位置にあったとする。また、惑星の公転周期をT,恒星の速度の視線方向成分を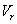 とする。
とする。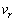 と
と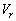 をtの関数として、その概形を
をtの関数として、その概形を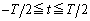 の範囲でグラフに描け。ただし、観測者に対して遠ざかる向きを
の範囲でグラフに描け。ただし、観測者に対して遠ざかる向きを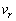 と
と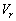 の正の向きに選ぶものとする。
の正の向きに選ぶものとする。 Ⅱ 惑星からの光は弱すぎて観測することは困難である。しかし、恒星からの光を観測することによって、惑星の存在を知ることができる。この間接的な惑星検出の方法では、運動する恒星が発する光の波長は、音源が動いた場合の音の波長と同様に、ドップラー効果によって変化することを利用する。ここでは、恒星が静止している場合には波長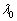 の光を発するものとして以下の問に答えよ。
の光を発するものとして以下の問に答えよ。 (1) 惑星が角度θ の位置にあるときに恒星が発する光を観測者が測定したところ、波長はλであった。光速度をcとして、波長の変化量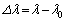 をθ の関数として求めよ。
をθ の関数として求めよ。 (2) II(1)で求めた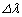 は時間変動する。
は時間変動する。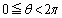 の範囲で
の範囲で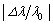 の最大値が
の最大値が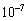 以上であれば、現在の観測技術で
以上であれば、現在の観測技術で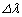 の時間変動を検出することができる。このことから、惑星の存在を知ることが可能であるためにaが満たすべき条件式を求めよ。
の時間変動を検出することができる。このことから、惑星の存在を知ることが可能であるためにaが満たすべき条件式を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 天文学の最前線の話題を問題にしている点では興味深い問題ですが、Ⅰ(1)は、もともと高校の範囲では解答不能な問題を無理に入試問題に焼き直しているために、問題文が不適切であるように思います。受験生としては、高校の範囲として勉強してきた条件下で考え、以下のような詳細な検討を省略して直観的に解答してよいと思われます。
Ⅰ(1) 点Cから見たときの、惑星、恒星の加速度をα,β とし、恒星の位置Pから惑星の位置Qまでの距離をrとします(問題文にあるように、恒星は点Cに位置するのではなく、恒星と惑星の距離もaではないことに注意)。恒星と惑星の間には、大きさ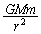 の万有引力が働きます。
の万有引力が働きます。 惑星に働く力は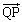 方向に働くので、
方向に働くので、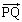 方向での惑星の運動方程式は、
方向での惑星の運動方程式は、 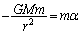 ・・・①
・・・①恒星に働く力は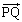 方向に働くので、
方向に働くので、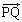 方向での恒星の運動方程式は、
方向での恒星の運動方程式は、 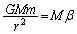 ・・・②
・・・②①+②より、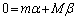 (これは、系に外力が働いておらず運動量の変化が0で、運動量が保存されることを意味します)これより、惑星と恒星の重心Rの位置:
(これは、系に外力が働いておらず運動量の変化が0で、運動量が保存されることを意味します)これより、惑星と恒星の重心Rの位置: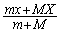 を時間tで2回微分すると、
を時間tで2回微分すると、 よって、惑星と恒星の重心Rは、等速直線運動を行うか静止することになります(等加速度運動を参照)。Cから見て、惑星と恒星の重心Rが等速直線運動をすると、いずれは、RはCからどんどん離れていくことになるので、惑星の運動がCを中心とする等速円運動になり得ません。従って、重心RはCから見て静止しています。
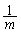 ×①-
×①-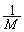 ×②を作ると、
×②を作ると、 両辺を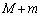 で割り、
で割り、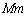 をかけると、
をかけると、 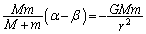 ・・・③
・・・③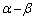 は、恒星Pから見た惑星の相対加速度を表します(相対運動を参照)が、③式は、恒星Pから見たときに、質量
は、恒星Pから見た惑星の相対加速度を表します(相対運動を参照)が、③式は、恒星Pから見たときに、質量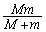 の惑星が大きさ
の惑星が大きさ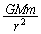 の万有引力を受けて運動する形をしているので、恒星Pから見て、惑星はPを焦点とする楕円軌道を描きながら運動します。
の万有引力を受けて運動する形をしているので、恒星Pから見て、惑星はPを焦点とする楕円軌道を描きながら運動します。
惑星Qは、Cを中心とする半径aの円周上に位置するので、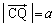 です。また、
です。また、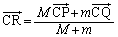 より、
より、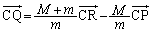 ,よって、
,よって、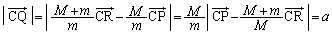 ∴
∴ 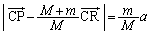
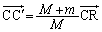 は定ベクトルなので、
は定ベクトルなので、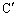 は定点であり、これは、
は定点であり、これは、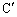 を中心とする半径
を中心とする半径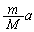 の円を表します。恒星も円運動しています。重心Rは、両円の中心を結ぶ線分
の円を表します。恒星も円運動しています。重心Rは、両円の中心を結ぶ線分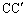 をM:mに内分する点です。
をM:mに内分する点です。
惑星の運動は等速円運動ですが、このためには、惑星は一定の大きさの向心力を受けることになります。ということは、①式の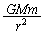 は一定値であって、恒星と惑星の距離rは一定です。
は一定値であって、恒星と惑星の距離rは一定です。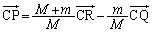 より、
より、これが一定であるためには、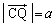 より、点Cと重心Rが一致
より、点Cと重心Rが一致し、
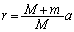
・・・④,つまり、点
Cが線分PQをm:Mに内分する点でなければなりません。
以上より、
惑星と恒星、定点Cの位置関係:恒星と惑星と点Cは一直線上にあって、恒星と惑星を結ぶ線分をm:Mに内分する点(両者の重心)が点Cとなる。 ......[答]理由:惑星と恒星を合わせた系に外力が働かず、運動量が変化しない。また、惑星は等速円運動するので系の運動量の和はゼロ。よって、Cから見て、恒星と惑星の重心は移動せず、惑星に一定の万有引力が働くことから、重心は定点Cに一致する。......[答]
(2) 恒星と定点Cとの距離は、(1)の結果と④より、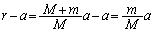 ......[答]
......[答] 半径aの等速円運動の向心加速度は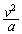 で、惑星の運動方程式は、
で、惑星の運動方程式は、 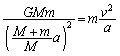 ∴
∴ 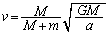 ......[答]
......[答]恒星の向心加速度は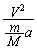 で、恒星の運動方程式は、
で、恒星の運動方程式は、 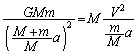 ∴
∴ 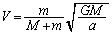 ......[答]
......[答](惑星と恒星の運動量の和が0,つまり、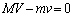 であることからも求められます)
であることからも求められます) (3) 充分遠方の観測者とCを結ぶ直線を結ぶ直線(視線方向)と、惑星の速度ベクトルとのなす角は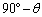 であって、惑星の速度の視線方向成分は、右図より、
であって、惑星の速度の視線方向成分は、右図より、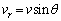 ......[答]
......[答] (4) (1)より、恒星の速度は、惑星の速度の向きとちょうど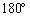 逆の向きで、恒星の速度の視線方向成分は、
逆の向きで、恒星の速度の視線方向成分は、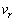 と符号が正反対になり、
と符号が正反対になり、
Ⅱ(1) 波長λ,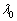 の光の振動数は
の光の振動数は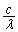 ,
,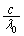 です。光源の近づく方向の速度成分は、
です。光源の近づく方向の速度成分は、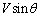 なので、ドップラー効果の公式より、
なので、ドップラー効果の公式より、 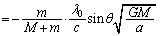 ......[答]
......[答]
∴ 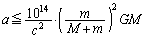 ......[答]
......[答]
(3) 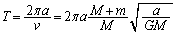
(2)の結果より、
∴ 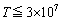 [s] ......[答]
[s] ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。