���啨��'07�N�O��[3]
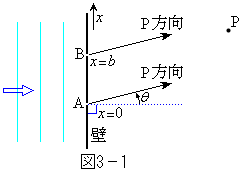 �@�}3�|1�̂悤�ɁA���ʏ�ŁA�g��λ�̔g��������E�ɂ܂������i�ݕǂɐ����ɏՓ˂��Ă���B�ǂɉ�����������x�����Ƃ��A�ǂɂ͎��R�ɂ����Ԃ��J���邱�Ƃ��ł���悤�ɂȂ��Ă���Ƃ���B�����Ԃ�ʂ����g��ǂ̉E���̓_�Ŋϑ�����B�ȉ��̖�ɓ�����B
�@�}3�|1�̂悤�ɁA���ʏ�ŁA�g��λ�̔g��������E�ɂ܂������i�ݕǂɐ����ɏՓ˂��Ă���B�ǂɉ�����������x�����Ƃ��A�ǂɂ͎��R�ɂ����Ԃ��J���邱�Ƃ��ł���悤�ɂȂ��Ă���Ƃ���B�����Ԃ�ʂ����g��ǂ̉E���̓_�Ŋϑ�����B�ȉ��̖�ɓ�����B
�T�@�_P�͏[�������ɂ���Ƃ��A�}3�|1�̂悤��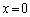 ���猩��P�����̊p�x��θ �Ƃ���B��T(1)�C(2)�ŊJ���邷���Ԃ͂��ׂē������Ƃ���B�܂��A���̂����Ԃ̕��͔g��λ�ɔ�ׂď������̂ŁA�e�����Ԃ���́A�����𒆐S�Ƃ���~�`�g���}�̉E���ɍL�����Ă����ƍl���Ă悢�B
���猩��P�����̊p�x��θ �Ƃ���B��T(1)�C(2)�ŊJ���邷���Ԃ͂��ׂē������Ƃ���B�܂��A���̂����Ԃ̕��͔g��λ�ɔ�ׂď������̂ŁA�e�����Ԃ���́A�����𒆐S�Ƃ���~�`�g���}�̉E���ɍL�����Ă����ƍl���Ă悢�B (1) �ǂ�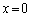 �̈ʒu�ɂ�����A���J���A�킸���ɂ��ꂽ�ʒux (
�̈ʒu�ɂ�����A���J���A�킸���ɂ��ꂽ�ʒux (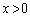 )�ɂ�����B���J����B������B���J����ʒu����������x�̐��̕����ɓ������Ă����ƁA
)�ɂ�����B���J����B������B���J����ʒu����������x�̐��̕����ɓ������Ă����ƁA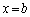 �ɂȂ����Ƃ��A����܂ŐU�����Ă����_P�ł̐��ʂ����߂ē����Ȃ��Ȃ����Bb��λ��θ ��p���ĕ\���B�������_P�͏\���ɉ����̂ŁA������B���猩��P�����̊p�x��θ �Ƃ��Ă悢�B
�ɂȂ����Ƃ��A����܂ŐU�����Ă����_P�ł̐��ʂ����߂ē����Ȃ��Ȃ����Bb��λ��θ ��p���ĕ\���B�������_P�͏\���ɉ����̂ŁA������B���猩��P�����̊p�x��θ �Ƃ��Ă悢�B �U�@���ɂ����Ԃ̕����L���ꍇ���l���悤�B�_P�͖�T�Ɠ����ʒu�ɂ���Ƃ���B�����Ԃ̈���̒[��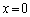 �C�����̒[��
�C�����̒[��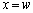 �Ƃ���(�}3�|2)�B�ȉ��̖�ɂ��ẮA�����ԓ��̊e�_����~�`�g(�f���g)���E�ɍL�����Ă����A���̏d�ˍ��킹���_P�ł̐��ʂ̐U���ɂȂ�ƍl����B
�Ƃ���(�}3�|2)�B�ȉ��̖�ɂ��ẮA�����ԓ��̊e�_����~�`�g(�f���g)���E�ɍL�����Ă����A���̏d�ˍ��킹���_P�ł̐��ʂ̐U���ɂȂ�ƍl����B (1) �����ԓ��̂���ʒu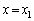 (
(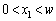 )����_P�܂ł̋����ƁA�����Ԃ̒[
)����_P�܂ł̋����ƁA�����Ԃ̒[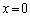 ����_P�܂ł̋����̍����A
����_P�܂ł̋����̍����A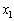 ��θ ��p���ĕ\���B
��θ ��p���ĕ\���B (2) 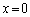 ����o���~�`�g�̕ψʂ��_P�Ń[���ł���u�ԂɁA�����ԓ��̊e�_
����o���~�`�g�̕ψʂ��_P�Ń[���ł���u�ԂɁA�����ԓ��̊e�_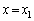 (
(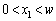 )���炭��~�`�g�̂��ׂĂ̕ψʂ��_P�œ������ł���(���ߍ���)���߂ɂ́A�����Ԃ̕�w�͂ǂ̂悤�ȏ��������Ă��Ȃ���Ȃ�Ȃ����B
)���炭��~�`�g�̂��ׂĂ̕ψʂ��_P�œ������ł���(���ߍ���)���߂ɂ́A�����Ԃ̕�w�͂ǂ̂悤�ȏ��������Ă��Ȃ���Ȃ�Ȃ����B (3) �����Ԃ̕���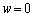 ����
����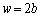 �܂ő��₵���Ƃ��_P�ł̔g�̐U���͂ǂ̂悤�ɕω����邩�A���R��t���ē�����B������b�͖�T(1)�ŋ��߂��l�ł���B
�܂ő��₵���Ƃ��_P�ł̔g�̐U���͂ǂ̂悤�ɕω����邩�A���R��t���ē�����B������b�͖�T(1)�ŋ��߂��l�ł���B 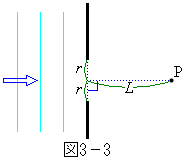 �V�@���x�͓_P�͕ǂ̋߂��ɂ���Ƃ��A�ǂƂ̋�����L�Ƃ���B�}3�|3�̂悤�ɁA�_P�̐^���ʂɂ����Ԃ��J����B���̂����Ԃ̕����[�����瑝�₵�Ă����ƁA����
�V�@���x�͓_P�͕ǂ̋߂��ɂ���Ƃ��A�ǂƂ̋�����L�Ƃ���B�}3�|3�̂悤�ɁA�_P�̐^���ʂɂ����Ԃ��J����B���̂����Ԃ̕����[�����瑝�₵�Ă����ƁA����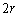 �ɂȂ����Ƃ��_P�ł̐U�����ő�ɂȂ����Br��L��λ��p���ĕ\���B
�ɂȂ����Ƃ��_P�ł̐U�����ő�ɂȂ����Br��L��λ��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� 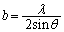 ......[��]
......[��] (2) A���痈��g��B���痈��g�͊��Ɏ�ߍ����Ă���̂ŁAC���痈��g��D���痈��g����ߍ����悢�Ƃ������ƂɂȂ�܂��B������D��x���W��d�Ƃ���ƁA���̏����́A���҂��o�H��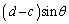 �����g���Ƃ������ƂŁA
�����g���Ƃ������ƂŁA
 ��
�� 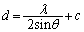 ......[��]
......[��]�U(1) P���\�������ɂ��邱�Ƃ���A�T(1)�Ɠ��l�ɁA�E�}���A�����̍��́A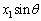 ......[��]
......[��]
(2) �����Ԃ����[�ł̌o�H�������g���ȉ��ł���AA (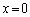 )����o���~�`�g���ψ���P�ɂ����ă[���̂Ƃ��ɁA�����Ԃ̊e�_���炭��~�`�g���ψ����������ɂȂ�܂�(�o�H�������g���ȉ��Ƃ������Ƃ́A�ʑ�����π�ȉ��Ƃ������Ƃł��B
)����o���~�`�g���ψ���P�ɂ����ă[���̂Ƃ��ɁA�����Ԃ̊e�_���炭��~�`�g���ψ����������ɂȂ�܂�(�o�H�������g���ȉ��Ƃ������Ƃ́A�ʑ�����π�ȉ��Ƃ������Ƃł��B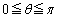 �ł����
�ł����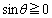 �Ƃ����Ƃ��납��l���Ă�������)�B
�Ƃ����Ƃ��납��l���Ă�������)�B �E�}���A�����Ԃ̗��[�̓_����P�܂ł��o�H����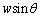 �Ȃ̂ŁA
�Ȃ̂ŁA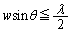
�� 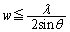 ......[��]�@(�܂�A�T(1)���A
......[��]�@(�܂�A�T(1)���A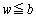 �ł�)
�ł�) (3) �U(2)�̏���(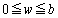 )����������Ă���Ԃ́A�����Ԃ�ʉ߂���g�̋��ߍ������ʂɂ��Aw��傫������ƁA�����Ԃ̕����L����ʉ߂���g�������邱�Ƃɂ���āAP�ɂ������U���͎���ɑ傫���Ȃ�A
)����������Ă���Ԃ́A�����Ԃ�ʉ߂���g�̋��ߍ������ʂɂ��Aw��傫������ƁA�����Ԃ̕����L����ʉ߂���g�������邱�Ƃɂ���āAP�ɂ������U���͎���ɑ傫���Ȃ�A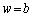 �̂Ƃ��ɍő�ɂȂ�܂��B
�̂Ƃ��ɍő�ɂȂ�܂��B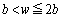 �ɂ����ẮA�����Ԃ�ʉ߂���g�̒��ɑł������������ʂ��N���āAw��傫������ƁAP�ɂ������U���͎���ɏ������Ȃ�܂��B
�ɂ����ẮA�����Ԃ�ʉ߂���g�̒��ɑł������������ʂ��N���āAw��傫������ƁAP�ɂ������U���͎���ɏ������Ȃ�܂��B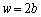 �̂Ƃ��ɁA�����Ԃ̉�������ʉ߂���g�Ə㔼����ʉ߂���g���t�ʑ�(�ʑ��̃Y����π)�ƂȂ�A�U���͍ŏ��ɂȂ�܂�(�E�})�B
�̂Ƃ��ɁA�����Ԃ̉�������ʉ߂���g�Ə㔼����ʉ߂���g���t�ʑ�(�ʑ��̃Y����π)�ƂȂ�A�U���͍ŏ��ɂȂ�܂�(�E�})�B 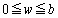 �ɂ����Ă͋��ߍ����g�������A
�ɂ����Ă͋��ߍ����g�������A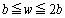 �ɂ����Ă͑ł����������g�������Ă���̂ŁA
�ɂ����Ă͑ł����������g�������Ă���̂ŁA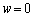 ���玟��ɑ�������
���玟��ɑ�������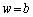 �ōő�ƂȂ�A
�ōő�ƂȂ�A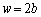 �܂Ō�������B ......[��]
�܂Ō�������B ......[��]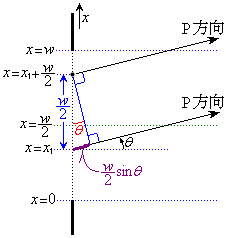 �Q�l�@�E�}�̂悤�ɁA�����Ԃ��㔼���Ɖ������ɕ����āA���ꂼ�ꂩ�痈��g���l���A�P�X���b�g�̌��ʂׂ܂��B
�Q�l�@�E�}�̂悤�ɁA�����Ԃ��㔼���Ɖ������ɕ����āA���ꂼ�ꂩ�痈��g���l���A�P�X���b�g�̌��ʂׂ܂��B
�������̒���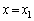 �̈ʒu����P�ɂ���g�ƁA�㔼����
�̈ʒu����P�ɂ���g�ƁA�㔼����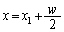 (
(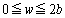 )�̈ʒu����P�ɂ���g���o�H���́A
)�̈ʒu����P�ɂ���g���o�H���́A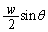 �C�g����λ�Ƃ���ƁA���̌o�H���ɂ���ʑ��̃Y��δ �́A�T(1)�̌��ʂ�p���āA
�C�g����λ�Ƃ���ƁA���̌o�H���ɂ���ʑ��̃Y��δ �́A�T(1)�̌��ʂ�p���āA�g��������T�Ƃ��āA�U���̈Ⴂ�����ė��g���d�ˍ��킹��ƁA
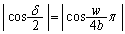 �̒l�ɂ���āAP�ɂ�����g���U����]���ł��܂��B
�̒l�ɂ���āAP�ɂ�����g���U����]���ł��܂��B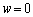 ����
����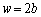 �܂ŕς��Ƃ��A
�܂ŕς��Ƃ��A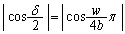 �́A1����0�܂ŕω����܂��B
�́A1����0�܂ŕω����܂��B
�����Ԃ�2�ɕ�����Ƃ��A�㔼�����痈��g�Ɖ��������痈��g�������ɂ��A�g�����ߍ������ʂ́A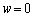 �ɂ����čő�ŁA
�ɂ����čő�ŁA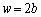 �ɂ����čŏ��ɂȂ�܂��B
�ɂ����čŏ��ɂȂ�܂��B
�]���āA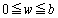 �ɂ����āAw��傫������Ƃ���P���U�����傫���Ȃ�̂́A�P�X���b�g�Ƃ��Ă̌��ʂł͂Ȃ��A�����Ԃ�ʉ߂��Ċ�����g�̗ʂ����������Ƃɂ���Ă���̂ł��B
�ɂ����āAw��傫������Ƃ���P���U�����傫���Ȃ�̂́A�P�X���b�g�Ƃ��Ă̌��ʂł͂Ȃ��A�����Ԃ�ʉ߂��Ċ�����g�̗ʂ����������Ƃɂ���Ă���̂ł��B
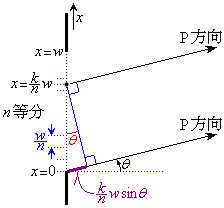 �E�}�̂悤�ɁAw��������x�̑傫�����Ƃ��āA�����Ԃ�n�������A�e�������炭��g���������邱�Ƃ��l���Ă݂܂��B�����Ԃ�ʉ߂���g���U�����e��������
�E�}�̂悤�ɁAw��������x�̑傫�����Ƃ��āA�����Ԃ�n�������A�e�������炭��g���������邱�Ƃ��l���Ă݂܂��B�����Ԃ�ʉ߂���g���U�����e��������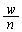 �ɔ�Ⴗ��Ƃ��܂��B
�ɔ�Ⴗ��Ƃ��܂��B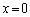 ���痈��g��k�Ԗڂ̕������炭��g���o�H����
���痈��g��k�Ԗڂ̕������炭��g���o�H���� �ł��B
�ł��B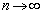 �Ƃ���ƁAP�ɂ����鍇���g�́A�敪���ϖ@�ɂ��A
�Ƃ���ƁAP�ɂ����鍇���g�́A�敪���ϖ@�ɂ��A�U(2)(3)�ɂ����āA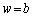 �̂Ƃ���P�ɂ������U�����ő�ɂȂ����̂́A�����Ԃ̏�[��P�Ƃ������A���[��P�Ƃ������̍���
�̂Ƃ���P�ɂ������U�����ő�ɂȂ����̂́A�����Ԃ̏�[��P�Ƃ������A���[��P�Ƃ������̍���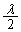 �ɂȂ�悤�Ȉʒu�W����������ł��B
�ɂȂ�悤�Ȉʒu�W����������ł��B
�]���Đ}3�|3�ɂ����Ă��A�����Ԃ̏�[��P�Ƃ������A�����Ԃ̒��S��P�Ƃ������̍������g���̂Ƃ��ɁA
P�ɂ������U�����ő�ɂȂ�͂��ł��B�E�}���A 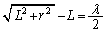 ��
�� 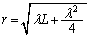 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B