������w2007�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
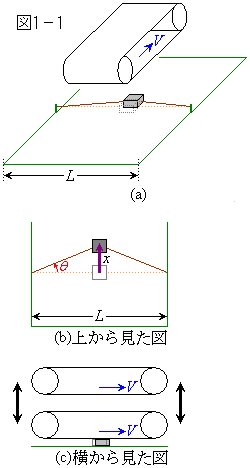 [1]�@�o�C�I�����̌��͋|�ł����邱�Ƃɂ��U������B�|�Ă�͂⓮���������̉e�����A�}1�|1�Ɏ������f���ōl���Ă݂悤�B����L�̌y������F�Ő����ɒ���A���̒����Ɏ���m�̔������t����B���́A���������̏�ԂŐ����ʂƐڂ��Ă���A���̗��[�����Ԑ����̐�����������Ȃ߂炩�ɓ������Ƃ��ł���B�}1�|1(b)�̂悤�ɁA���̗��[�����Ԑ����̒��_(�����̎n�_)�̕ψ�x�̌��_�Ƃ��A�����̌�����ψʂ���ї͂̐��̌����Ƃ���B���̕ψʂ͎��̒����ɔ�ׂď\���������A���̒��͈͂��ƌ��Ȃ����Ƃ��ł���B�}1�|1(c)�̂悤�ɁA���̏�ɂ͐��̌����Ɉ��̑���V�œ����Ă���x���g������A���ɐڐG�����邱�Ƃ��ł���悤�ɂȂ��Ă���B�x���g���猩�����̑��x���x���g�Ɣ��̑��Α��x�ƒ�`����B�x���g�Ɣ����ڐG���Ă����Ԃő��Α��x��0�̂Ƃ��A�x���g���甠�ɐÎ~���C�͂������B�Î~���C�W����μ�Ƃ���B�x���g���甠�ɓ��������C�͂���ю��Ɣ��ɓ�����C��R������B
[1]�@�o�C�I�����̌��͋|�ł����邱�Ƃɂ��U������B�|�Ă�͂⓮���������̉e�����A�}1�|1�Ɏ������f���ōl���Ă݂悤�B����L�̌y������F�Ő����ɒ���A���̒����Ɏ���m�̔������t����B���́A���������̏�ԂŐ����ʂƐڂ��Ă���A���̗��[�����Ԑ����̐�����������Ȃ߂炩�ɓ������Ƃ��ł���B�}1�|1(b)�̂悤�ɁA���̗��[�����Ԑ����̒��_(�����̎n�_)�̕ψ�x�̌��_�Ƃ��A�����̌�����ψʂ���ї͂̐��̌����Ƃ���B���̕ψʂ͎��̒����ɔ�ׂď\���������A���̒��͈͂��ƌ��Ȃ����Ƃ��ł���B�}1�|1(c)�̂悤�ɁA���̏�ɂ͐��̌����Ɉ��̑���V�œ����Ă���x���g������A���ɐڐG�����邱�Ƃ��ł���悤�ɂȂ��Ă���B�x���g���猩�����̑��x���x���g�Ɣ��̑��Α��x�ƒ�`����B�x���g�Ɣ����ڐG���Ă����Ԃő��Α��x��0�̂Ƃ��A�x���g���甠�ɐÎ~���C�͂������B�Î~���C�W����μ�Ƃ���B�x���g���甠�ɓ��������C�͂���ю��Ɣ��ɓ�����C��R������B
�T�@�x���g�Ɣ����ڐG���Ă��Ȃ��Ƃ��̔��̉^�����l����B�}1�|1(b)�̂悤�ɁA���̗��[�����Ԑ����Ǝ����Ȃ��p��θ [rad]�Ƃ���B�K�v������A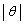 ��1�ɔ�ׂď\���ɏ������Ƃ��ɐ��藧�ߎ���
��1�ɔ�ׂď\���ɏ������Ƃ��ɐ��藧�ߎ��� ��p���Ă悢�B
��p���Ă悢�B (1) �����甠�ɓ��������͂̑傫����F�Cθ ��p���ĕ\���B�܂��A���̕����͂̑傫����L�CF�Cx��p���ĕ\���B
(2) ���ɏ����ψʂ��������x��^����ƁA���͒P�U��������B�P�U���̎���T��L�CF�Cm��p���ĕ\���B
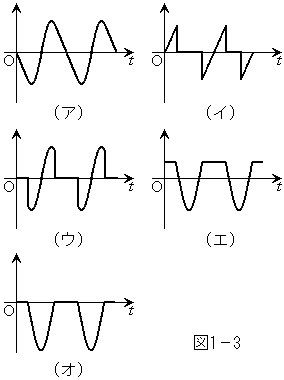 (1)
(1) 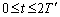 �͈̔͂ŁA(a)���̑��x�A(b)�x���g�Ɣ��̑��Α��x�A(c)�����甠�ɓ��������́A(d)�x���g���甠�ɓ����Î~���C�́A��\���}���A�}1�|3��(�A)�`(�I)���炻�ꂼ��I�ׁB
�͈̔͂ŁA(a)���̑��x�A(b)�x���g�Ɣ��̑��Α��x�A(c)�����甠�ɓ��������́A(d)�x���g���甠�ɓ����Î~���C�́A��\���}���A�}1�|3��(�A)�`(�I)���炻�ꂼ��I�ׁB(2) �����x���g�ɑ��Ċ���n�߂�_P�ł̔��̕ψ�s��L�CF�Cμ�CN��p���ĕ\���B
(3) PQ�Ԃł́A���͖�T(2)�ōl�����P�U���Ɠ����^��������B���̍ő�ψ�A��L�CF�Cm�CV�Cμ�CN��p���ĕ\���B
(4) �x���g���甠�ɓ��������R��N��傫������ƁA���̍ő�ψ�A�Ɣ���1�����̉^���ɗv���鎞��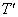 �́A���ꂼ��A�傫���Ȃ邩�A�������Ȃ邩�A�ς��Ȃ����A�𗝗R�ƂƂ��ɓ�����B���R�̐����ɐ}��p���Ă悢�B
�́A���ꂼ��A�傫���Ȃ邩�A�������Ȃ邩�A�ς��Ȃ����A�𗝗R�ƂƂ��ɓ�����B���R�̐����ɐ}��p���Ă悢�B [��]
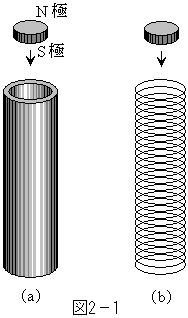 [2]�@�}2�|1(a)�̂悤�ɁA���̂łł�������̉~���������ɗ��ĂāA���̒��ɉ~���`�̎����m�ɂ���ɏ�ɂȂ�悤�ɂ��Ă����Ɨ�������A�₪�Ă�����̑����ŗ��������B����́A�����~������ʉ߂���Ƃ��A�d���U���ɂ�肻�̎���̓��̂ɓd��������邽�߂ł���B���̗������x���ǂ̂悤�Ɍ��܂邩�𗝉����邽�߂ɁA���̂̉~�����A�}2�|1(b)�̂悤�ɁA���Ԋu�Őςݏグ��ꂽ��������̕������̃����O�Œu�������čl���Ă݂�B�ȉ��̖�ɓ�����B
[2]�@�}2�|1(a)�̂悤�ɁA���̂łł�������̉~���������ɗ��ĂāA���̒��ɉ~���`�̎����m�ɂ���ɏ�ɂȂ�悤�ɂ��Ă����Ɨ�������A�₪�Ă�����̑����ŗ��������B����́A�����~������ʉ߂���Ƃ��A�d���U���ɂ�肻�̎���̓��̂ɓd��������邽�߂ł���B���̗������x���ǂ̂悤�Ɍ��܂邩�𗝉����邽�߂ɁA���̂̉~�����A�}2�|1(b)�̂悤�ɁA���Ԋu�Őςݏグ��ꂽ��������̕������̃����O�Œu�������čl���Ă݂�B�ȉ��̖�ɓ�����B
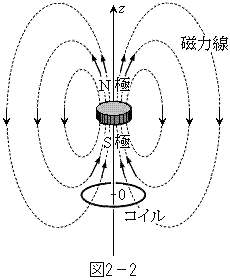 �T�@�܂��A�}2�|2�̂悤�ɁA1�̃����O�����������ɌŒ肳��Ă�����Ă���A���̃����O�̒��S���������̑���v�ʼn������ɒʂ蔲����ꍇ���l����Bz���W���A�����O�̒��S�����_�Ƃ��āA��������������ɂȂ�悤�ɂƂ�B����z���ɉ����āAz���̕��̌����ɉ^�����邱�Ƃɒ��ӂ���B
�T�@�܂��A�}2�|2�̂悤�ɁA1�̃����O�����������ɌŒ肳��Ă�����Ă���A���̃����O�̒��S���������̑���v�ʼn������ɒʂ蔲����ꍇ���l����Bz���W���A�����O�̒��S�����_�Ƃ��āA��������������ɂȂ�悤�ɂƂ�B����z���ɉ����āAz���̕��̌����ɉ^�����邱�Ƃɒ��ӂ���B(1) ���������O�ɋ߂Â��Ƃ��Ɖ�������Ƃ��A���ꂼ��ɂ����āA�����O�ɗ����d���̌����ƁA���̗U���d�������ɋy�ڂ��͂̌�������B�d���̌����͏�����ɐi�މE�˂�����]��������𐳂Ƃ��A�����ɂ���ĕ\���B 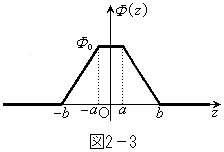 (2) ���̒��S�̍��W��z�ɂ���Ƃ��A
(2) ���̒��S�̍��W��z�ɂ���Ƃ��A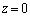 �ɒu���ꂽ�����O���т�����
�ɒu���ꂽ�����O���т�����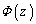 ���A�}2�|3�̂悤�ɑ�`���ŋߎ�����B���Ȃ킿�����́A���
���A�}2�|3�̂悤�ɑ�`���ŋߎ�����B���Ȃ킿�����́A���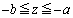 ��0����ő�l
��0����ő�l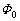 �Ɉ��̊����ő������A���
�Ɉ��̊����ő������A���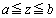 �ōő�l
�ōő�l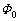 ����Ă�0�Ɉ��̊����Ō�������Ƃ���B�����Ŏ����̐��̌�����������ɂƂ����B�����ʉ߂���O��ɁA���̃����O�Ɉꎞ�I�ɗU���N�d�͂������B���̑傫����
����Ă�0�Ɉ��̊����Ō�������Ƃ���B�����Ŏ����̐��̌�����������ɂƂ����B�����ʉ߂���O��ɁA���̃����O�Ɉꎞ�I�ɗU���N�d�͂������B���̑傫����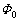 �Cv�Ca�Cb��p���ĕ\���B
�Cv�Ca�Cb��p���ĕ\���B(3) �����O����̒�R��R�Ƃ����Ƃ��A�U���N�d�͂ɂ���ė����d���̎��ԕω�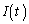 �̃O���t��`���B�����O�ɓd��������n�߂鎞��������t�̌��_�ɂƂ�A�d���̐����Ƒ傫���A�d�����ω����鎞���L����B�������A�����O�̎��ȃC���_�N�^���X�͖������Ă悢�B
�̃O���t��`���B�����O�ɓd��������n�߂鎞��������t�̌��_�ɂƂ�A�d���̐����Ƒ傫���A�d�����ω����鎞���L����B�������A�����O�̎��ȃC���_�N�^���X�͖������Ă悢�B
�U�@���ɁA�}2�|1(b)�̂悤�ɁA���������ɖ�T�ōl���������O�𖧂ɐςݏグ�A���̒����T�Ɠ��������ʉ߂���ꍇ���l����B���������̒P�ʒ���������̃����O�̐���n�Ƃ���B
(1) �����O�ɓd���������ƃW���[���M����������B��������v�ŗ�������Ƃ��A�ςݏグ��ꂽ�����O�S�̂���P�ʎ��ԓ�����ɔ�������W���[���M�����߂�B
(2) ���̎��ʂ�M�C�d�͉����x��g�Ƃ����Ƃ��A�G�l���M�[�̕ۑ�����p����Ǝ������̑����ŗ������邱�Ƃ��킩��B���̑���v�����߂�B�������A���̂Ƃ���C�̒�R�͖����ł�����̂Ƃ���B
�V�@�}2�|1(a)�ŁA����N�ɂƂr�ɂ��t�ɂ��Ď������s���ƁA���͂ǂ̂悤�ȉ^�����s�����A���̗��R�������B [��]
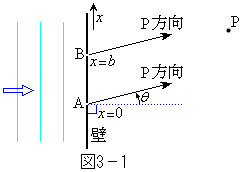 [3]�@�}3�|1�̂悤�ɁA���ʏ�ŁA�g��λ�̔g��������E�ɂ܂������i�ݕǂɐ����ɏՓ˂��Ă���B�ǂɉ�����������x�����Ƃ��A�ǂɂ͎��R�ɂ����Ԃ��J���邱�Ƃ��ł���悤�ɂȂ��Ă���Ƃ���B�����Ԃ�ʂ����g��ǂ̉E���̓_�Ŋϑ�����B�ȉ��̖�ɓ�����B
[3]�@�}3�|1�̂悤�ɁA���ʏ�ŁA�g��λ�̔g��������E�ɂ܂������i�ݕǂɐ����ɏՓ˂��Ă���B�ǂɉ�����������x�����Ƃ��A�ǂɂ͎��R�ɂ����Ԃ��J���邱�Ƃ��ł���悤�ɂȂ��Ă���Ƃ���B�����Ԃ�ʂ����g��ǂ̉E���̓_�Ŋϑ�����B�ȉ��̖�ɓ�����B
�T�@�_P�͏[�������ɂ���Ƃ��A�}3�|1�̂悤��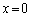 ���猩��P�����̊p�x��θ �Ƃ���B��T(1)�C(2)�ŊJ���邷���Ԃ͂��ׂē������Ƃ���B�܂��A���̂����Ԃ̕��͔g��λ�ɔ�ׂď������̂ŁA�e�����Ԃ���́A�����𒆐S�Ƃ���~�`�g���}�̉E���ɍL�����Ă����ƍl���Ă悢�B
���猩��P�����̊p�x��θ �Ƃ���B��T(1)�C(2)�ŊJ���邷���Ԃ͂��ׂē������Ƃ���B�܂��A���̂����Ԃ̕��͔g��λ�ɔ�ׂď������̂ŁA�e�����Ԃ���́A�����𒆐S�Ƃ���~�`�g���}�̉E���ɍL�����Ă����ƍl���Ă悢�B (1) �ǂ�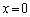 �̈ʒu�ɂ�����A���J���A�킸���ɂ��ꂽ�ʒux (
�̈ʒu�ɂ�����A���J���A�킸���ɂ��ꂽ�ʒux (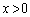 )�ɂ�����B���J����B������B���J����ʒu����������x�̐��̕����ɓ������Ă����ƁA
)�ɂ�����B���J����B������B���J����ʒu����������x�̐��̕����ɓ������Ă����ƁA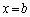 �ɂȂ����Ƃ��A����܂ŐU�����Ă����_P�ł̐��ʂ����߂ē����Ȃ��Ȃ����Bb��λ��θ ��p���ĕ\���B�������_P�͏\���ɉ����̂ŁA������B���猩��P�����̊p�x��θ �Ƃ��Ă悢�B
�ɂȂ����Ƃ��A����܂ŐU�����Ă����_P�ł̐��ʂ����߂ē����Ȃ��Ȃ����Bb��λ��θ ��p���ĕ\���B�������_P�͏\���ɉ����̂ŁA������B���猩��P�����̊p�x��θ �Ƃ��Ă悢�B �U�@���ɂ����Ԃ̕����L���ꍇ���l���悤�B�_P�͖�T�Ɠ����ʒu�ɂ���Ƃ���B�����Ԃ̈���̒[��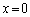 �C�����̒[��
�C�����̒[��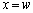 �Ƃ���(�}3�|2)�B�ȉ��̖�ɂ��ẮA�����ԓ��̊e�_����~�`�g(�f���g)���E�ɍL�����Ă����A���̏d�ˍ��킹���_P�ł̐��ʂ̐U���ɂȂ�ƍl����B
�Ƃ���(�}3�|2)�B�ȉ��̖�ɂ��ẮA�����ԓ��̊e�_����~�`�g(�f���g)���E�ɍL�����Ă����A���̏d�ˍ��킹���_P�ł̐��ʂ̐U���ɂȂ�ƍl����B (1) �����ԓ��̂���ʒu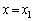 (
(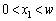 )����_P�܂ł̋����ƁA�����Ԃ̒[
)����_P�܂ł̋����ƁA�����Ԃ̒[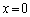 ����_P�܂ł̋����̍����A
����_P�܂ł̋����̍����A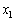 ��θ ��p���ĕ\���B
��θ ��p���ĕ\���B (2) 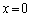 ����o���~�`�g�̕ψʂ��_P�Ń[���ł���u�ԂɁA�����ԓ��̊e�_
����o���~�`�g�̕ψʂ��_P�Ń[���ł���u�ԂɁA�����ԓ��̊e�_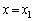 (
(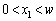 )���炭��~�`�g�̂��ׂĂ̕ψʂ��_P�œ������ł���(���ߍ���)���߂ɂ́A�����Ԃ̕�w�͂ǂ̂悤�ȏ��������Ă��Ȃ���Ȃ�Ȃ����B
)���炭��~�`�g�̂��ׂĂ̕ψʂ��_P�œ������ł���(���ߍ���)���߂ɂ́A�����Ԃ̕�w�͂ǂ̂悤�ȏ��������Ă��Ȃ���Ȃ�Ȃ����B (3) �����Ԃ̕���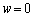 ����
����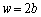 �܂ő��₵���Ƃ��_P�ł̔g�̐U���͂ǂ̂悤�ɕω����邩�A���R��t���ē�����B������b�͖�T(1)�ŋ��߂��l�ł���B
�܂ő��₵���Ƃ��_P�ł̔g�̐U���͂ǂ̂悤�ɕω����邩�A���R��t���ē�����B������b�͖�T(1)�ŋ��߂��l�ł���B 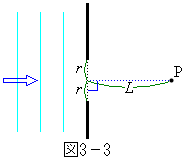 �V�@���x�͓_P�͕ǂ̋߂��ɂ���Ƃ��A�ǂƂ̋�����L�Ƃ���B�}3�|3�̂悤�ɁA�_P�̐^���ʂɂ����Ԃ��J����B���̂����Ԃ̕����[�����瑝�₵�Ă����ƁA����
�V�@���x�͓_P�͕ǂ̋߂��ɂ���Ƃ��A�ǂƂ̋�����L�Ƃ���B�}3�|3�̂悤�ɁA�_P�̐^���ʂɂ����Ԃ��J����B���̂����Ԃ̕����[�����瑝�₵�Ă����ƁA����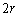 �ɂȂ����Ƃ��_P�ł̐U�����ő�ɂȂ����Br��L��λ��p���ĕ\���B
�ɂȂ����Ƃ��_P�ł̐U�����ő�ɂȂ����Br��L��λ��p���ĕ\���B
�e�⌟��
[1](��������)�@���̖��ŗv������Ă����b�����́A2�͂̍����A�����́A�P�U���̉^���������A���Α��x�̍l�����A�Î~���C�́A�͊w�I�G�l���M�[�ۑ����Ƃ��������Ƃł��B���x���Ƃ��ẮA���ȏ����x���ŏ[���ł��B�U(4)����⍂���x���ł����A��b����������ł��Ă�����ł���A�{��͊������s�\�ł͂���܂���B
�������Ȃ���A��b�����̗����ɕs�[���ȓ_������ƁA���鏊�Ɉ���������|�C���g���U��߂��Ă��܂��B
�U(1)�̓O���t��I�Ԃ����ł����A��蕶�̒P�U���̃O���t�ɘf�킳���ƁA���Ⴂ�����˂܂���B���̉^���̏A�x���g�ɑ��Ăǂ������Ă��邩�A�x���g�ɑ��ĐÎ~���Ă���ΐÎ~���C�͂������A�Ƃ��������I������������܂Ȃ��ƁA�����͍���ł��B
�U(2)�͗͂̂荇���̎��A(3)�͗͊w�I�G�l���M�[�ۑ����̎������������Ȃ̂ł����A��͂蔠�̉^���̏�����ł������Ƃ��K�{�ł��B
�����܂ł́A���ȏ�����������ǂݍ���ł�����������ł��܂��B���W�̉��ߓǂ݂��ĈËL����悤�ȓw�͕͂����ł͖��ɂ͗����܂���B�܂��͊�b���ł߂邱�Ƃ�����Ƃ������Ƃ���������Ɠ��ɓ���Ă����Ă��������B
�U(4)�́A�����R�͂̑召�ɂ���āA��蕶���̒P�U���̃O���t���ǂ��Ȃ�̂��A�Ƃ������Ƃ��}���ł���A�قږ��炩�Ȃ��Ƃł��B�U�����ω����Ă��P�U���̎������ς��Ȃ����ƁA����o���Ƃ��ɘA���I�ɑ��x���ω����邱�Ƃ����߂Ă���A���R��������邱�Ƃ��ł���ł��傤�B
���ǂ��悤�ł����A�����_���Ƃ��邽�߂ɂ́A�܂��́A���ȏ����o�C�u���Ƃ��ďn�ǂ��A��b�����╨���@�����������藝�����邱�Ƃɗ͂�����悤�ɂ��Ă��������B
[2](��������)�@�d���C�̖��ł����A'07�N�O��[1]�Ɠ��l�ɁA���ȏ����x���̊�b�����̗������������ł��B�����ȎZ�I��p����悤�ȂƂ���͂���܂���B��蕶�ŏq�ׂ��Ă��镨���I���A�}��������Ă��Ė��m�ŁA��ӂ̔c���ł܂Â��悤�Ȃ��Ƃ��Ȃ��ł��傤�B�r���A�G�l���M�[�ۑ����l����Ƃ��낪����܂����A��蕶���Ɂu�G�l���M�[�ۑ�����p����Ɓv�Ƃ����w��������A�����˘f�����Ƃ͂Ȃ��͂��ł��B
�ɂ�������炸�A����������肪����̓����ɏo�Ă���A�Ƃ������Ƃ́A������ƌ����ǁA�����̊�{���������l�����Ȃ肢��Ƃ������Ƃ��낤�Ǝv���܂��B������������������悤�ɂȂ肽���Əł�A��b�����̗������s�[���Ȃ܂܁A�������W�Ȃǂɓ������Ď��Ԃ����_�Ɏg�����Ƃ̂Ȃ��悤�ɂ��Ē��������Ǝv���܂��B
[3](��������)�@�e07�O��[1]�A'07�O��[2]�Ƃ͈�]���ē��ł��B�T����U(1)�܂ł́A�o�H���A���̏������Ă��邾���Ȃ̂ŃX���i������Ǝv���܂��B
���͂܂��A�U(2)�ł��B��蕶�̌����Ă��邱�Ƃ����߂�ł��傤���H�����ԓ��̂���ʒu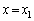 ����P�_�ɂ���Ă���g�́A(1)���A
����P�_�ɂ���Ă���g�́A(1)���A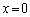 ����P�_�ɂ���Ă���g�ƌo�H��
����P�_�ɂ���Ă���g�ƌo�H��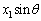 �������Ă��܂����A���̕������ʑ����i��ł��܂��B�U���̈Ⴂ�����čl����ƁA
�������Ă��܂����A���̕������ʑ����i��ł��܂��B�U���̈Ⴂ�����čl����ƁA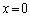 ����P�_�ɗ���g��
����P�_�ɗ���g��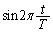 ���Ƃ��āA
���Ƃ��āA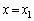 ����P�_�ɗ���g��
����P�_�ɗ���g��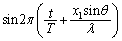 �ł��B��蕶�ł́A
�ł��B��蕶�ł́A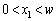 ���݂������ׂĂ̓_����P�_�ɂ���Ă���g�ɂ��āA
���݂������ׂĂ̓_����P�_�ɂ���Ă���g�ɂ��āA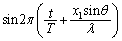 �̒l���������ɂȂ�悤��w�͂ǂ��Ȃ�̂��A�ƁA�����Ă��܂��B
�̒l���������ɂȂ�悤��w�͂ǂ��Ȃ�̂��A�ƁA�����Ă��܂��B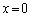 ����P�_�ɗ���g�̕ψʂ��[���ƂȂ�u�ԁA�ƌ����Ă���̂ŁA
����P�_�ɗ���g�̕ψʂ��[���ƂȂ�u�ԁA�ƌ����Ă���̂ŁA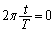 �Ƃ��čl����ƁA
�Ƃ��čl����ƁA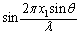 �����������Ƃ������Ƃ́A
�����������Ƃ������Ƃ́A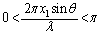 �C�܂�A
�C�܂�A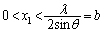 �Ƃ������Ƃł��B
�Ƃ������Ƃł��B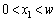 �Ȃ̂ŁAw�ɂ��āA
�Ȃ̂ŁAw�ɂ��āA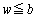 �ƂȂ�܂��B�����́A��ӂ����߂Đ������̃O���t���v�������ׂ�A�ł���ł��傤�B
�ƂȂ�܂��B�����́A��ӂ����߂Đ������̃O���t���v�������ׂ�A�ł���ł��傤�B
�U(3)�́A�قƂ�ǂ̎����P�X���b�g�̊��������l���ă~�X���A�����҂͂قƂ�ǂ��Ȃ����낤�Ǝv���܂��B���Z�����̔g���ł́A2�g�������ċ��ߍ������ǂ����A�Ƃ������Ƃ������܂����A�����̔g���d�ˍ��킳�ꂽ�ꍇ�ɐU�����ǂ��Ȃ邩�A�Ƃ����g��ϕ��������͈̂����܂���(�����Č����A�z�C�w���X�̌��������ł�)�B���[���ƃv���X�̂��̂𑫂����킹��Α�����A�}�C�i�X�̂��̂𑫂��悤�ɂȂ�ƌ���A�Ƃ��������̂��ƂŁA�U(2)�̈Ӗ����Âɍl������Z�͈̔͂łł��Ȃ��킯�ł͂���܂��A������ƁA�������Ƃ��Ė����Ȃ̂ł͂Ȃ����A�Ƃ����C�����܂��B
�V�́A�U(3)��p���čl����̂ŁA�U(3)���~�X����Ǝ����I�ɃA�E�g�ɂȂ�܂��B
���ǁA���̖��́A��ӂ�c���ł��邩�ǂ����ŇU(2)�̏o���s�o�������������x�ŁA�قƂ�ǂ̎����T�ƇU(1)�𐳉��A�U(3)�ƇV�͕s�����ƂȂ��Ă��܂��A�S���������Ȃ������̂ł͂Ȃ����Ǝv���܂��B
���̗��ꂩ�炷��ƁA�ǂ����Z�I�I�Ȃ��̂ł͇U(3)�͑Ώ��ł��Ȃ��̂ł��B���ȏ����x���̊�b�������K�b�`���ł߂āA���_�ł�����͊m���ɓ��_�����Ă������A�Ƃ������ƂɂȂ�ł��傤�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B