東大物理'19年前期[3]
光の屈折に関する以下の設問Ⅰ,Ⅱに答えよ。問題文中の屈折率は真空に対する屈折率(絶対屈折率)とする。また、角度は全てラジアンで表す。光源からは全方位に光が放射されているものとする。光の反射は無視してよい。
 Ⅰ 図3-1に示すように、媒質1(屈折率
Ⅰ 図3-1に示すように、媒質1(屈折率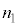 )と媒質2(屈折率
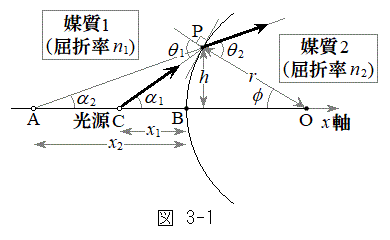
)と媒質2(屈折率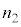 )の境界での光の屈折を考える。境界は点Oを中心とする半径rの球面の一部であり、左に凸とする。点Oと光源(点C)を通る直線をx軸とし、球面がx軸と交わる点をBとする。光源は点Bから左に
)の境界での光の屈折を考える。境界は点Oを中心とする半径rの球面の一部であり、左に凸とする。点Oと光源(点C)を通る直線をx軸とし、球面がx軸と交わる点をBとする。光源は点Bから左に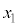 だけ離れており、そこから発した図中の太矢印方向の光線は、x軸から高さhの球面上の点Pで屈折する。このときの入射角を
だけ離れており、そこから発した図中の太矢印方向の光線は、x軸から高さhの球面上の点Pで屈折する。このときの入射角を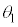 ,屈折角を
,屈折角を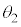 とする。
とする。境界の右側から光源を見ると、あたかも光源が点A(点Bから左に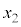 だけ離れた位置)にあるように見える。本設問Ⅰおよび次の設問Ⅱでは、これを「見かけ上の光源」と呼ぶことにする。以下、入射角が微小となる光線を考える。すなわち、図中の角度
だけ離れた位置)にあるように見える。本設問Ⅰおよび次の設問Ⅱでは、これを「見かけ上の光源」と呼ぶことにする。以下、入射角が微小となる光線を考える。すなわち、図中の角度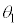 ,
,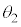 ,
,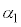 ,
,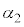 ,ϕについて微小角度βに対する近似式
,ϕについて微小角度βに対する近似式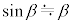 が成り立ち、
が成り立ち、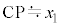 ,
,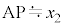 と近似できる場合を考える。以下の問いに答えよ。
と近似できる場合を考える。以下の問いに答えよ。 (2) 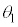 ,
,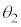 をそれぞれ
をそれぞれ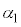 ,
,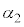 ,ϕの中から必要なものを用いて表せ。
,ϕの中から必要なものを用いて表せ。 (3) 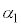 ,
,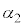 ,ϕをそれぞれ
,ϕをそれぞれ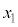 ,
,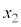 ,r,hの中から必要なものを用いて表せ。
,r,hの中から必要なものを用いて表せ。 (4) 問(1)~(3)で得た関係式を組み合わせることで(式1)が導かれる。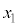 ,
,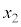 を用いて空欄
を用いて空欄 ,
, を埋め、この式を完成させよ。
を埋め、この式を完成させよ。 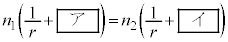 ・・・(式1)
・・・(式1)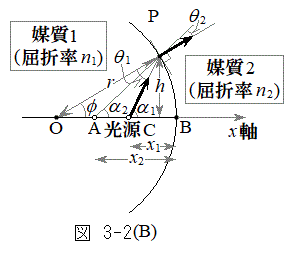
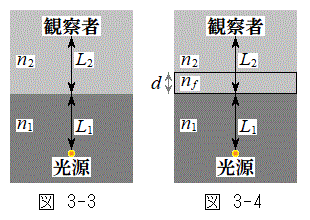 Ⅱ(1) 図3-3に示すように、屈折率
Ⅱ(1) 図3-3に示すように、屈折率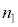 の媒質1に光源があり、屈折率
の媒質1に光源があり、屈折率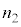 の媒質2に観察者がいる。媒質1と媒質2の境界は平面であり、(式1)においてrが非常に大きい場合(
の媒質2に観察者がいる。媒質1と媒質2の境界は平面であり、(式1)においてrが非常に大きい場合(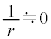 )とみなすことができる。境界から光源までの距離を
)とみなすことができる。境界から光源までの距離を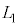 ,境界から観察者までの距離を
,境界から観察者までの距離を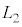 ,光源から観察者までの距離を
,光源から観察者までの距離を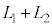 とするとき、観察者から設問Ⅰで述べた「見かけ上の光源」までの距離を
とするとき、観察者から設問Ⅰで述べた「見かけ上の光源」までの距離を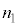 ,
,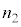 ,
,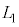 ,
,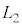 を用いて表せ。
を用いて表せ。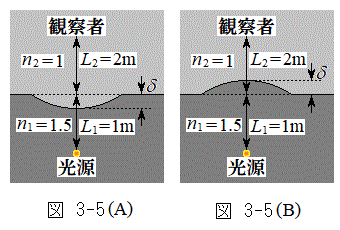 (3) 設問Ⅱ(2)で置いた板を取り除いたのち、媒質1と媒質2の境界を図3-5の(A)または(B)のように変形させた。変形した部分は半径rの球の一部とみなすことができる。ただし、境界面の最大変位δは
(3) 設問Ⅱ(2)で置いた板を取り除いたのち、媒質1と媒質2の境界を図3-5の(A)または(B)のように変形させた。変形した部分は半径rの球の一部とみなすことができる。ただし、境界面の最大変位δは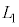 ,
,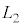 に比べて十分小さく無視してよい。いま、
に比べて十分小さく無視してよい。いま、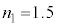 ,
,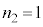 ,
,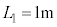 ,
,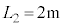 とする。このとき、変形した部分を通して見ると、観察者から4mの位置に「見かけ上の光源」が見えた。この場合の球面は下に凸[図3-5(A)]、または上に凸[図3-5(B)]のうちのいずれであるか。(A)または(B)の記号で答えよ。さらに、rの値を求めよ。
とする。このとき、変形した部分を通して見ると、観察者から4mの位置に「見かけ上の光源」が見えた。この場合の球面は下に凸[図3-5(A)]、または上に凸[図3-5(B)]のうちのいずれであるか。(A)または(B)の記号で答えよ。さらに、rの値を求めよ。(4) 設問Ⅱ(3)の状況で、観察者の位置に厚さの無視できる薄いレンズを一つ置き、その上から見たところ、「見かけ上の光源」が光源の位置(レンズから3mの位置)に見えた。このとき、凸レンズと凹レンズののどちらを用いたか答えよ。また、このレンズの焦点距離を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 考えるところはありません。言われた通りに解答するだけです。
Ⅰ(1) 屈折の法則より、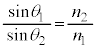 ,
,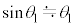 ,
,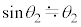 として、
として、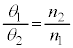 ......[答]
......[答]
(2) 図3-1より、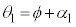 ,
,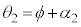 ......[答]
......[答]
(3) 図3-1において、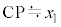 ,
,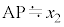 より、
より、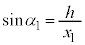 ,
,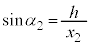 ,
,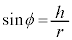 ,
,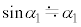 ,
,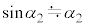 ,
,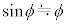 より、
より、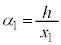 ,
,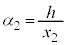 ,
,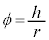 ......[答]
......[答]
(4) (1)の結果より、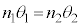
これに、(2),(3)の結果を代入することにより、
∴ 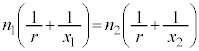 ・・・(式1) [ア]
・・・(式1) [ア] 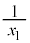 [イ]
[イ] 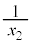 ......[答]
......[答]
(5) 図3-2(A)と図3-1との違いは、(2)の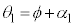 ,
,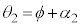 が、
が、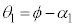 ,
,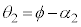 となる点です。よって、(式1)は、図3-2(A)では、
となる点です。よって、(式1)は、図3-2(A)では、 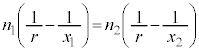 ......[答] ・・・①
......[答] ・・・①図3-2(B)と図3-1との違いは、(2)の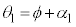 ,
,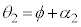 が、
が、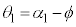 ,
,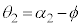 となる点です。よって、(式1)は、図3-2(B)では、
となる点です。よって、(式1)は、図3-2(B)では、 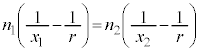 ......[答] ・・・②
......[答] ・・・②
Ⅱ(1) (式1)で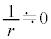 とすると、
とすると、 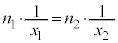 ∴
∴ 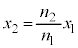 ・・・③
・・・③③は、①,②で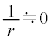 としても得られます。本問では、③を、屈折率
としても得られます。本問では、③を、屈折率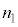 の媒質中に光源があって、屈折率
の媒質中に光源があって、屈折率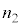 の媒質中に観察者がいる場合について、光源までの真の距離
の媒質中に観察者がいる場合について、光源までの真の距離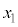 と、「見かけ上の光源」までの距離
と、「見かけ上の光源」までの距離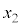 の関係式として考えよう、ということになります。
の関係式として考えよう、ということになります。
図3-3では、③で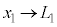 とすると、「見かけ上の光源」までの距離は、
とすると、「見かけ上の光源」までの距離は、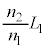 となります。観察者から「見かけ上の光源」までの距離は、
となります。観察者から「見かけ上の光源」までの距離は、 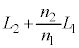 ......[答]
......[答]
(2) 屈折率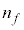 の透明板内最下部に光源があり、これを屈折率
の透明板内最下部に光源があり、これを屈折率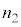 の媒質2から見るときの「見かけ上の光源」までの距離は、③で
の媒質2から見るときの「見かけ上の光源」までの距離は、③で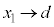 とすると、
とすると、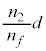
このとき、観察者から「見かけ上の光源」までの距離は、(1)の結果より、
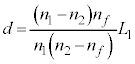 ......[答]
......[答]
(3) 図3-5[A]では、光源の方に向って凸になるので、観察者から「見かけ上の光源」までの距離を4として、(式1)において、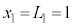 ,
,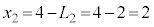 ,
,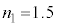 ,
,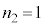 とすると、
とすると、 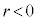 となってしまうので不適です。
となってしまうので不適です。
図3-5[B]では、光源の方に向って凹になり、①でも②でも同じ式であって、ここで、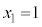 ,
,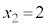 ,
,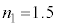 ,
,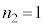 とすると、
とすると、となるので、この場合の球面は(B) ......[答],また、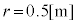 ......[答]
......[答]
(4) レンズの公式: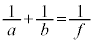 において、
において、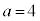 ,
,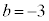 (像が光源側にできる)とすると、
(像が光源側にできる)とすると、 よって、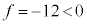 となり、レンズは凹レンズ ......[答],その焦点距離は、12[m] ......[答]
となり、レンズは凹レンズ ......[答],その焦点距離は、12[m] ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
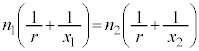 ・・・(式1) [ア]
・・・(式1) [ア] 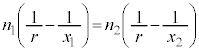 ......[答] ・・・①
......[答] ・・・①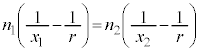 ......[答] ・・・②
......[答] ・・・②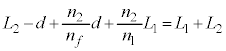
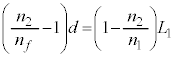
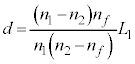 ......[答]
......[答]