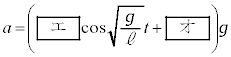東京大学2019年前期物理入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 水平な床面上にとったx軸に沿って動く台車の上の物体の運動について以下の設問Ⅰ,Ⅱに答えよ。
 Ⅰ 図1-1に示すように、台車の上にばね定数kを持ち質量の無視できるばねを介して質量mの物体が取り付けられており、物体は台車上を滑らかに動く。台車に固定された座標軸yを、ばねの自然長の位置を原点として、x軸と同じ向きにとる。ばねはy軸方向にのみ伸び縮みし、ばねと台車は十分長い。台車はx軸方向に任意の加速度aで強制的に運動させることができる。
Ⅰ 図1-1に示すように、台車の上にばね定数kを持ち質量の無視できるばねを介して質量mの物体が取り付けられており、物体は台車上を滑らかに動く。台車に固定された座標軸yを、ばねの自然長の位置を原点として、x軸と同じ向きにとる。ばねはy軸方向にのみ伸び縮みし、ばねと台車は十分長い。台車はx軸方向に任意の加速度aで強制的に運動させることができる。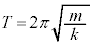 として以下の設問に答えよ。
として以下の設問に答えよ。 表1-1| | 時刻t | 台車の加速度a |
| 加速区間 | 0~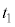 | 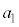 |
| 等速区間 | 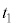 ~ ~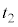 | 0 |
| 減速区間 | 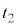 ~ ~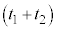 | 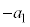 |
(1) 台車が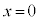 ,物体が
,物体が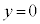 で静止している状態から、台車を表1-1に示す加速度で強制的に運動させる。加速度の大きさ
で静止している状態から、台車を表1-1に示す加速度で強制的に運動させる。加速度の大きさ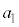 は定数である。時刻
は定数である。時刻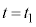 における台車の速度、および時刻
における台車の速度、および時刻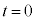 から
から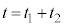 までの間に台車が移動する距離を求めよ。
までの間に台車が移動する距離を求めよ。 (2) 物体が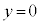 で静止している状態から、表1-1で
で静止している状態から、表1-1で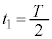 ,
,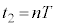 (nは自然数)として台車を動かす。時刻
(nは自然数)として台車を動かす。時刻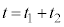 における物体のy座標および台車に対する相対速度を求めよ。
における物体のy座標および台車に対する相対速度を求めよ。
(3) 次に台車を止めた状態で物体を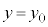 (
(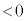 )にいったん固定したのち、
)にいったん固定したのち、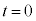 で物体を静かに放し、表1-2に示す加速度で台車を強制的に運動させる。
で物体を静かに放し、表1-2に示す加速度で台車を強制的に運動させる。 加速度の大きさ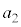 がある定数のとき、時刻
がある定数のとき、時刻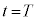 において物体のy座標は
において物体のy座標は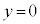 となり、台車に対する物体の相対速度も0となる。
となり、台車に対する物体の相対速度も0となる。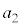 の値および
の値および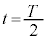 における物体のy座標を求めよ。
における物体のy座標を求めよ。
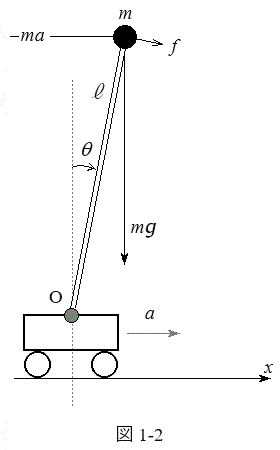 Ⅱ 手のひらの上に棒を立て、棒が倒れないように手を動かす遊びがある。このしくみを図1-2に示す倒立振子で考える。倒立振子は質量の無視できる変形しない長さ
Ⅱ 手のひらの上に棒を立て、棒が倒れないように手を動かす遊びがある。このしくみを図1-2に示す倒立振子で考える。倒立振子は質量の無視できる変形しない長さ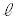 の細い棒の先端に質量mの質点を取り付けたものとし、台車上の点Oを支点としてx軸を含む鉛直面内で滑らかに動くことができる。倒立振子の傾きは鉛直上向きから図1-2の時計回り角度θ(ラジアン)で表す。θの大きさは十分に小さく、
の細い棒の先端に質量mの質点を取り付けたものとし、台車上の点Oを支点としてx軸を含む鉛直面内で滑らかに動くことができる。倒立振子の傾きは鉛直上向きから図1-2の時計回り角度θ(ラジアン)で表す。θの大きさは十分に小さく、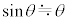 ,
,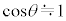 の近似が成り立つ。台車は倒立振子の運動の影響を受けることなく任意の加速度aで強制的に動かせるものとする。重力加速度の大きさを
の近似が成り立つ。台車は倒立振子の運動の影響を受けることなく任意の加速度aで強制的に動かせるものとする。重力加速度の大きさを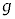 ,
,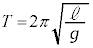 として以下の設問に答えよ。
として以下の設問に答えよ。(1) 台車が加速度aで加速しているとき、台車上で見ると、θだけ傾いた倒立振子の先端の質点には、図1-2に示すように重力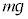 と慣性力
と慣性力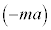 が作用している。質点に働く力の棒に垂直な成分f をθ,a,m,
が作用している。質点に働く力の棒に垂直な成分f をθ,a,m,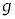 を用いて表せ。ただし、f の正の向きはθが増える向きと同じとする。
を用いて表せ。ただし、f の正の向きはθが増える向きと同じとする。
 (2) 時刻
(2) 時刻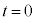 で台車は静止しており、倒立振子を
で台車は静止しており、倒立振子を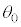 傾けて静止させた状態から始まる運動を考える。時刻
傾けて静止させた状態から始まる運動を考える。時刻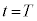 で台車が静止し、かつ倒立振子が
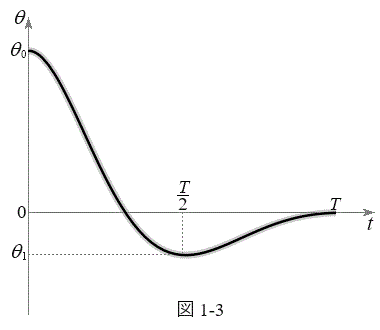
で台車が静止し、かつ倒立振子が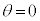 で静止するようにしたい。そのために倒立振子を図1-3に示すように運動させる。すなわち単振動の半周期分の運動で
で静止するようにしたい。そのために倒立振子を図1-3に示すように運動させる。すなわち単振動の半周期分の運動で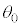 から0を通過して
から0を通過して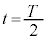 で
で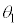 に至り、続いて
に至り、続いて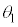 から振幅の異なる単振動の半周期分の運動ののち、
から振幅の異なる単振動の半周期分の運動ののち、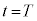 において
において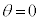 に戻り静止する。このような運動となるように加速度aを変化させる。
に戻り静止する。このような運動となるように加速度aを変化させる。
以下の式中の空欄 から
から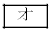 に当てはまる式を選択肢①から⑰の中から選べ。選択肢は繰り返し使って良い。また空欄
に当てはまる式を選択肢①から⑰の中から選べ。選択肢は繰り返し使って良い。また空欄 から
から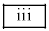 に当てはまる数式を書け。
に当てはまる数式を書け。
時刻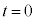 から
から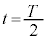 の間のθは
の間のθは と表される。このように単振動する質点にはたらく復元力Fは
である。この運動を実現するためには設問Ⅱ(1)で求めたf がFと等しければよいので加速度aは次の式となる。
この式の第1項が単振動の加速度と同じ形であることを考慮すると、時刻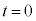 から
から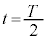 の台車の速度の変化
の台車の速度の変化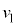 は
は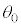 ,
,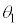 ,
,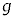 ,
,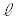 を用いて
を用いて となる。
時刻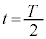 から
から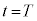 の運動についても単振動の半周期分であるので同様に考えれば、この区間の台車の速度の変化
の運動についても単振動の半周期分であるので同様に考えれば、この区間の台車の速度の変化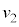 は
は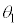 ,
,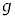 ,
,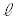 を用いて
を用いて となる。よって
を得る。
① 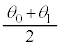 ②
② 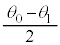 ③
③ 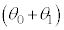 ④
④ 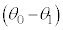 ⑤
⑤ 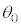 ⑥
⑥ 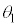 ⑦ 0 ⑧ π ⑨
⑦ 0 ⑧ π ⑨ 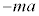 ⑩
⑩ 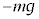 ⑪
⑪ 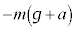 ⑫
⑫ 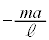 ⑬
⑬ 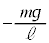 ⑭
⑭ 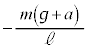 ⑮
⑮ 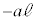 ⑯
⑯ 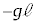 ⑰
⑰ 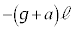
[解答へ]
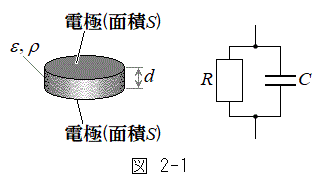 [2] 図2-1左に示すように、面積Sの薄い円板状の電極2枚を距離dだけ隔てて平行に配置し、誘電率ε,抵抗率ρの物質でできた面積S,厚さdの一様な円柱を電極間に挿入した。電極と円柱はすき間なく接触しており、電場は向かい合う電極間にのみに生じると考えてよい。電極の抵抗は無視できるものとする。この電極と円柱の組み合わせは、図2-1右に示すように、並列に接続された抵抗値Rの抵抗と電気容量Cのコンデンサーによって等価的に表現することができる。以下の設問に答えよ。
[2] 図2-1左に示すように、面積Sの薄い円板状の電極2枚を距離dだけ隔てて平行に配置し、誘電率ε,抵抗率ρの物質でできた面積S,厚さdの一様な円柱を電極間に挿入した。電極と円柱はすき間なく接触しており、電場は向かい合う電極間にのみに生じると考えてよい。電極の抵抗は無視できるものとする。この電極と円柱の組み合わせは、図2-1右に示すように、並列に接続された抵抗値Rの抵抗と電気容量Cのコンデンサーによって等価的に表現することができる。以下の設問に答えよ。
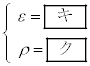
Ⅰ RとCをそれぞれε,ρ,S,dのうち必要なものを用いて表せ。
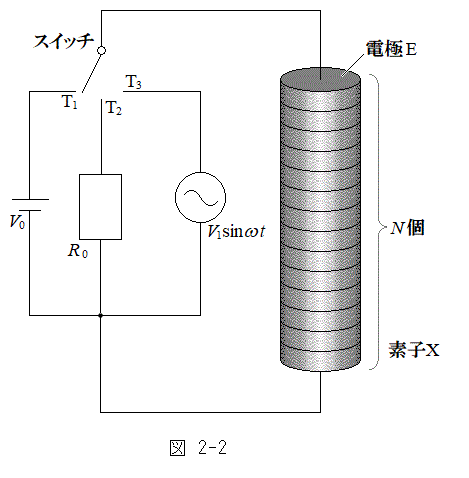 Ⅱ 図2-2に示すように上記の電極と円柱の組み合わせをN個積み重ねて接触させ、素子Xを構成した。スイッチを切り替えることによって、この素子Xに電圧
Ⅱ 図2-2に示すように上記の電極と円柱の組み合わせをN個積み重ねて接触させ、素子Xを構成した。スイッチを切り替えることによって、この素子Xに電圧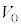 の直流電源、抵抗値
の直流電源、抵抗値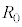 の抵抗、電圧
の抵抗、電圧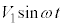 の交流電源のいずれかひとつを接続することができる。ωは角周波数、t は時間である。以下の設問(1)~(3)にはεとρは用いずに、N,R,Cのうち必要なものを含む式で解答せよ。
の交流電源のいずれかひとつを接続することができる。ωは角周波数、t は時間である。以下の設問(1)~(3)にはεとρは用いずに、N,R,Cのうち必要なものを含む式で解答せよ。(1) はじめにスイッチを端子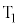 に接続して素子Xに直流電圧
に接続して素子Xに直流電圧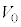 を加えた。スイッチを操作してから十分に長い時間が経過したとき、直流電源から素子Xに流れる電流の大きさと、素子Xの上端に位置する電極Eに蓄積される電気量を求めよ。
を加えた。スイッチを操作してから十分に長い時間が経過したとき、直流電源から素子Xに流れる電流の大きさと、素子Xの上端に位置する電極Eに蓄積される電気量を求めよ。 (2) 続いてスイッチを端子端子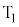 から
から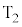 に切り替えたところ、抵抗
に切り替えたところ、抵抗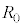 と素子Xに電流が流れた。ただしスイッチの操作は十分に短い時間内に行われ、スイッチを操作する間に素子X内の電極の電気量は変化しないものとする。スイッチを操作してから十分に長い時間が経過したところ、電流が流れなくなった。スイッチを端子
と素子Xに電流が流れた。ただしスイッチの操作は十分に短い時間内に行われ、スイッチを操作する間に素子X内の電極の電気量は変化しないものとする。スイッチを操作してから十分に長い時間が経過したところ、電流が流れなくなった。スイッチを端子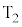 に接続してから電流が流れなくなるまでに抵抗
に接続してから電流が流れなくなるまでに抵抗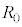 で生じたジュール熱を求めよ。また、素子Xを構成する電極と円柱の組み合わせの個数Nを増やして同様の操作を行ったとき、抵抗
で生じたジュール熱を求めよ。また、素子Xを構成する電極と円柱の組み合わせの個数Nを増やして同様の操作を行ったとき、抵抗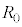 で発生するジュール熱はNの増加に対してどのように変化するかを次の①~④から一つ選べ。
で発生するジュール熱はNの増加に対してどのように変化するかを次の①~④から一つ選べ。 ① 単調に増加する ② 単調に減少する ③ 変化しない
④ 上記①~③のいずれでもない
(3) 次にスイッチを端子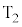 から
から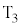 に切り替え、素子Xに交流電圧
に切り替え、素子Xに交流電圧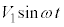 を加えた。スイッチを操作してから十分に長い時間が経過したとき、交流電源から素子Xへ流れる電流を求めよ。
を加えた。スイッチを操作してから十分に長い時間が経過したとき、交流電源から素子Xへ流れる電流を求めよ。
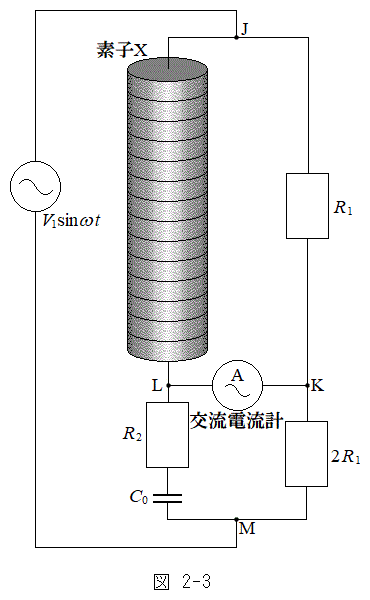 Ⅲ 設問Ⅱで用いた素子Xを構成する物質のεおよびρの値が未知であるとき、これの値を求めるためにブリッジ回路を用いる方法がある。図2-3のように素子X,設問Ⅱの交流電源、交流電流計、3つの抵抗と1つのコンデンサーを配置し、交流ブリッジ回路を構成した。抵抗値と電気容量の大きさを調節したところ、交流電流計に電流が流れなくなった。このとき、図2-3のように各抵抗の抵抗値は
Ⅲ 設問Ⅱで用いた素子Xを構成する物質のεおよびρの値が未知であるとき、これの値を求めるためにブリッジ回路を用いる方法がある。図2-3のように素子X,設問Ⅱの交流電源、交流電流計、3つの抵抗と1つのコンデンサーを配置し、交流ブリッジ回路を構成した。抵抗値と電気容量の大きさを調節したところ、交流電流計に電流が流れなくなった。このとき、図2-3のように各抵抗の抵抗値は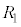 ,
,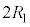 ,
,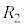 ,コンデンサーの電気容量は
,コンデンサーの電気容量は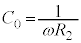 であった。次の
であった。次の から
から に入る適切な数式を書け。なお、J,K,L,Mは回路上の点を表す。
に入る適切な数式を書け。なお、J,K,L,Mは回路上の点を表す。
K-M間の電圧は である。このことを用いて、抵抗
である。このことを用いて、抵抗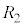 に流れる電流を、
に流れる電流を、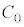 を含まない式で表すと、
を含まない式で表すと、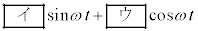 となる。一方、J-K間の電圧は
となる。一方、J-K間の電圧は であることから、J-L間を流れる電流をCやRを含む式で表すと
であることから、J-L間を流れる電流をCやRを含む式で表すと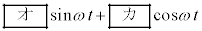 となる。以上のことから次式が得られる。
となる。以上のことから次式が得られる。 [解答へ]
[3] 光の屈折に関する以下の設問Ⅰ,Ⅱに答えよ。問題文中の屈折率は真空に対する屈折率(絶対屈折率)とする。また、角度は全てラジアンで表す。光源からは全方位に光が放射されているものとする。光の反射は無視してよい。
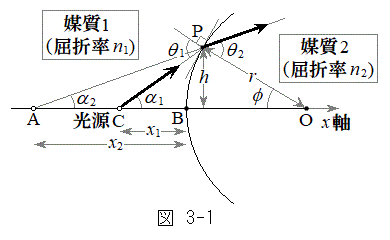 Ⅰ 図3-1に示すように、媒質1(屈折率
Ⅰ 図3-1に示すように、媒質1(屈折率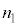 )と媒質2(屈折率
)と媒質2(屈折率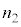 )の境界での光の屈折を考える。境界は点Oを中心とする半径rの球面の一部であり、左に凸とする。点Oと光源(点C)を通る直線をx軸とし、球面がx軸と交わる点をBとする。光源は点Bから左に
)の境界での光の屈折を考える。境界は点Oを中心とする半径rの球面の一部であり、左に凸とする。点Oと光源(点C)を通る直線をx軸とし、球面がx軸と交わる点をBとする。光源は点Bから左に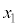 だけ離れており、そこから発した図中の太矢印方向の光線は、x軸から高さhの球面上の点Pで屈折する。このときの入射角を
だけ離れており、そこから発した図中の太矢印方向の光線は、x軸から高さhの球面上の点Pで屈折する。このときの入射角を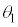 ,屈折角を
,屈折角を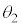 とする。
とする。境界の右側から光源を見ると、あたかも光源が点A(点Bから左に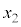 だけ離れた位置)にあるように見える。本設問Ⅰおよび次の設問Ⅱでは、これを「見かけ上の光源」と呼ぶことにする。以下、入射角が微小となる光線を考える。すなわち、図中の角度
だけ離れた位置)にあるように見える。本設問Ⅰおよび次の設問Ⅱでは、これを「見かけ上の光源」と呼ぶことにする。以下、入射角が微小となる光線を考える。すなわち、図中の角度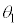 ,
,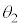 ,
,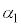 ,
,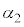 ,ϕについて微小角度βに対する近似式
,ϕについて微小角度βに対する近似式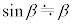 が成り立ち、
が成り立ち、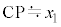 ,
,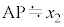 と近似できる場合を考える。以下の問いに答えよ。
と近似できる場合を考える。以下の問いに答えよ。 (2) 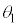 ,
,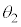 をそれぞれ
をそれぞれ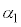 ,
,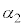 ,ϕの中から必要なものを用いて表せ。
,ϕの中から必要なものを用いて表せ。 (3) 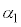 ,
,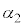 ,ϕをそれぞれ
,ϕをそれぞれ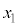 ,
,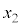 ,r,hの中から必要なものを用いて表せ。
,r,hの中から必要なものを用いて表せ。 (4) 問(1)~(3)で得た関係式を組み合わせることで(式1)が導かれる。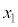 ,
,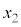 を用いて空欄
を用いて空欄 ,
, を埋め、この式を完成させよ。
を埋め、この式を完成させよ。 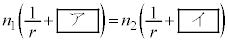 ・・・(式1)
・・・(式1)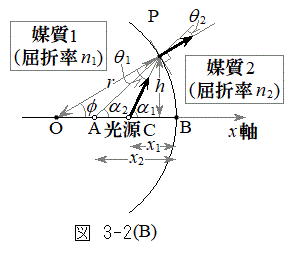
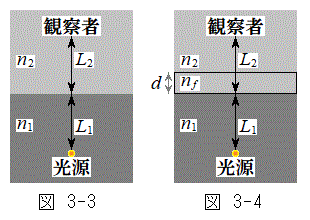 Ⅱ(1) 図3-3に示すように、屈折率
Ⅱ(1) 図3-3に示すように、屈折率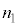 の媒質1に光源があり、屈折率
の媒質1に光源があり、屈折率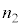 の媒質2に観察者がいる。媒質1と媒質2の境界は平面であり、(式1)においてrが非常に大きい場合(
の媒質2に観察者がいる。媒質1と媒質2の境界は平面であり、(式1)においてrが非常に大きい場合(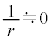 )とみなすことができる。境界から光源までの距離を
)とみなすことができる。境界から光源までの距離を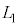 ,境界から観察者までの距離を
,境界から観察者までの距離を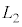 ,光源から観察者までの距離を
,光源から観察者までの距離を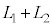 とするとき、観察者から設問Ⅰで述べた「見かけ上の光源」までの距離を
とするとき、観察者から設問Ⅰで述べた「見かけ上の光源」までの距離を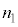 ,
,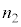 ,
,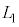 ,
,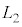 を用いて表せ。
を用いて表せ。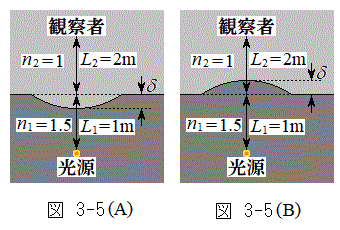 (3) 設問Ⅱ(2)で置いた板を取り除いたのち、媒質1と媒質2の境界を図3-5の(A)または(B)のように変形させた。変形した部分は半径rの球の一部とみなすことができる。ただし、境界面の最大変位δは
(3) 設問Ⅱ(2)で置いた板を取り除いたのち、媒質1と媒質2の境界を図3-5の(A)または(B)のように変形させた。変形した部分は半径rの球の一部とみなすことができる。ただし、境界面の最大変位δは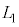 ,
,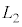 に比べて十分小さく無視してよい。いま、
に比べて十分小さく無視してよい。いま、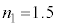 ,
,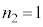 ,
,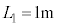 ,
,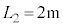 とする。このとき、変形した部分を通して見ると、観察者から4mの位置に「見かけ上の光源」が見えた。この場合の球面は下に凸[図3-5(A)]、または上に凸[図3-5(B)]のうちのいずれであるか。(A)または(B)の記号で答えよ。さらに、rの値を求めよ。
とする。このとき、変形した部分を通して見ると、観察者から4mの位置に「見かけ上の光源」が見えた。この場合の球面は下に凸[図3-5(A)]、または上に凸[図3-5(B)]のうちのいずれであるか。(A)または(B)の記号で答えよ。さらに、rの値を求めよ。(4) 設問Ⅱ(3)の状況で、観察者の位置に厚さの無視できる薄いレンズを一つ置き、その上から見たところ、「見かけ上の光源」が光源の位置(レンズから3mの位置)に見えた。このとき、凸レンズと凹レンズののどちらを用いたか答えよ。また、このレンズの焦点距離を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。