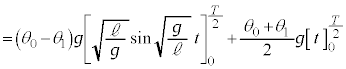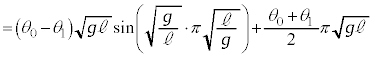東大物理'19年前期[1]
水平な床面上にとったx軸に沿って動く台車の上の物体の運動について以下の設問Ⅰ,Ⅱに答えよ。
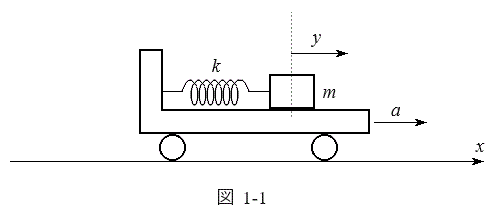 Ⅰ 図1-1に示すように、台車の上にばね定数kを持ち質量の無視できるばねを介して質量mの物体が取り付けられており、物体は台車上を滑らかに動く。台車に固定された座標軸yを、ばねの自然長の位置を原点として、x軸と同じ向きにとる。ばねはy軸方向にのみ伸び縮みし、ばねと台車は十分長い。台車はx軸方向に任意の加速度aで強制的に運動させることができる。
Ⅰ 図1-1に示すように、台車の上にばね定数kを持ち質量の無視できるばねを介して質量mの物体が取り付けられており、物体は台車上を滑らかに動く。台車に固定された座標軸yを、ばねの自然長の位置を原点として、x軸と同じ向きにとる。ばねはy軸方向にのみ伸び縮みし、ばねと台車は十分長い。台車はx軸方向に任意の加速度aで強制的に運動させることができる。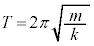 として以下の設問に答えよ。
として以下の設問に答えよ。 表1-1| | 時刻t | 台車の加速度a |
| 加速区間 | 0~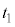 | 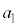 |
| 等速区間 | 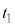 ~ ~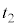 | 0 |
| 減速区間 | 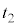 ~ ~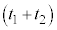 | 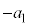 |
(1) 台車が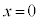 ,物体が
,物体が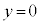 で静止している状態から、台車を表1-1に示す加速度で強制的に運動させる。加速度の大きさ
で静止している状態から、台車を表1-1に示す加速度で強制的に運動させる。加速度の大きさ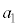 は定数である。時刻
は定数である。時刻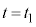 における台車の速度、および時刻
における台車の速度、および時刻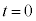 から
から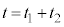 までの間に台車が移動する距離を求めよ。
までの間に台車が移動する距離を求めよ。 (2) 物体が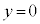 で静止している状態から、表1-1で
で静止している状態から、表1-1で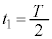 ,
,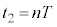 (nは自然数)として台車を動かす。時刻
(nは自然数)として台車を動かす。時刻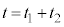 における物体のy座標および台車に対する相対速度を求めよ。
における物体のy座標および台車に対する相対速度を求めよ。
(3) 次に台車を止めた状態で物体を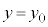 (
(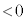 )にいったん固定したのち、
)にいったん固定したのち、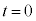 で物体を静かに放し、表1-2に示す加速度で台車を強制的に運動させる。
で物体を静かに放し、表1-2に示す加速度で台車を強制的に運動させる。 加速度の大きさ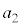 がある定数のとき、時刻
がある定数のとき、時刻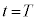 において物体のy座標は
において物体のy座標は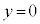 となり、台車に対する物体の相対速度も0となる。
となり、台車に対する物体の相対速度も0となる。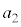 の値および
の値および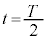 における物体のy座標を求めよ。
における物体のy座標を求めよ。
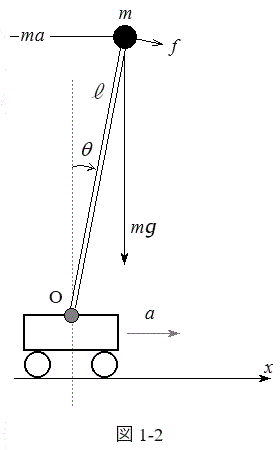 Ⅱ 手のひらの上に棒を立て、棒が倒れないように手を動かす遊びがある。このしくみを図1-2に示す倒立振子で考える。倒立振子は質量の無視できる変形しない長さ
Ⅱ 手のひらの上に棒を立て、棒が倒れないように手を動かす遊びがある。このしくみを図1-2に示す倒立振子で考える。倒立振子は質量の無視できる変形しない長さ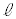 の細い棒の先端に質量mの質点を取り付けたものとし、台車上の点Oを支点としてx軸を含む鉛直面内で滑らかに動くことができる。倒立振子の傾きは鉛直上向きから図1-2の時計回り角度θ(ラジアン)で表す。θの大きさは十分に小さく、
の細い棒の先端に質量mの質点を取り付けたものとし、台車上の点Oを支点としてx軸を含む鉛直面内で滑らかに動くことができる。倒立振子の傾きは鉛直上向きから図1-2の時計回り角度θ(ラジアン)で表す。θの大きさは十分に小さく、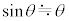 ,
,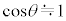 の近似が成り立つ。台車は倒立振子の運動の影響を受けることなく任意の加速度aで強制的に動かせるものとする。重力加速度の大きさを
の近似が成り立つ。台車は倒立振子の運動の影響を受けることなく任意の加速度aで強制的に動かせるものとする。重力加速度の大きさを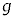 ,
,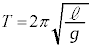 として以下の設問に答えよ。
として以下の設問に答えよ。(1) 台車が加速度aで加速しているとき、台車上で見ると、θだけ傾いた倒立振子の先端の質点には、図1-2に示すように重力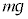 と慣性力
と慣性力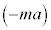 が作用している。質点に働く力の棒に垂直な成分f をθ,a,m,
が作用している。質点に働く力の棒に垂直な成分f をθ,a,m,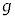 を用いて表せ。ただし、f の正の向きはθが増える向きと同じとする。
を用いて表せ。ただし、f の正の向きはθが増える向きと同じとする。
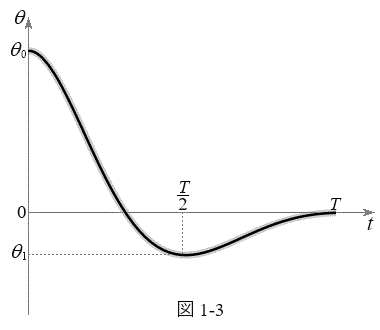 (2) 時刻
(2) 時刻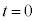 で台車は静止しており、倒立振子を
で台車は静止しており、倒立振子を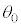 傾けて静止させた状態から始まる運動を考える。時刻
傾けて静止させた状態から始まる運動を考える。時刻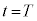 で台車が静止し、かつ倒立振子が
で台車が静止し、かつ倒立振子が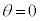 で静止するようにしたい。そのために倒立振子を図1-3に示すように運動させる。すなわち単振動の半周期分の運動で
で静止するようにしたい。そのために倒立振子を図1-3に示すように運動させる。すなわち単振動の半周期分の運動で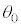 から0を通過して
から0を通過して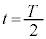 で
で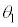 に至り、続いて
に至り、続いて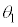 から振幅の異なる単振動の半周期分の運動ののち、
から振幅の異なる単振動の半周期分の運動ののち、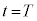 において
において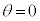 に戻り静止する。このような運動となるように加速度aを変化させる。
に戻り静止する。このような運動となるように加速度aを変化させる。
以下の式中の空欄 から
から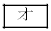 に当てはまる式を選択肢①から⑰の中から選べ。選択肢は繰り返し使って良い。また空欄
に当てはまる式を選択肢①から⑰の中から選べ。選択肢は繰り返し使って良い。また空欄 から
から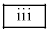 に当てはまる数式を書け。
に当てはまる数式を書け。
時刻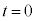 から
から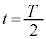 の間のθは
の間のθは と表される。このように単振動する質点にはたらく復元力Fは
である。この運動を実現するためには設問Ⅱ(1)で求めたf がFと等しければよいので加速度aは次の式となる。
この式の第1項が単振動の加速度と同じ形であることを考慮すると、時刻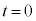 から
から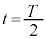 の台車の速度の変化
の台車の速度の変化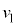 は
は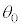 ,
,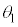 ,
,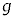 ,
,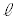 を用いて
を用いて となる。
時刻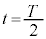 から
から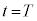 の運動についても単振動の半周期分であるので同様に考えれば、この区間の台車の速度の変化
の運動についても単振動の半周期分であるので同様に考えれば、この区間の台車の速度の変化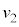 は
は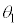 ,
,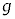 ,
,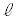 を用いて
を用いて となる。よって
を得る。
① 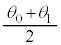 ②
② 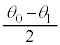 ③
③ 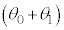 ④
④ 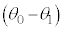 ⑤
⑤ 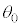 ⑥
⑥ 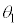 ⑦ 0 ⑧ π ⑨
⑦ 0 ⑧ π ⑨ 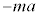 ⑩
⑩ 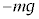 ⑪
⑪ 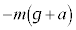 ⑫
⑫ 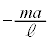 ⑬
⑬ 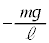 ⑭
⑭ 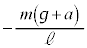 ⑮
⑮ 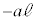 ⑯
⑯ 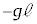 ⑰
⑰ 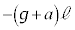
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 前半は、面倒ですが、慣性力がからむ単振動の基本問題です。後半は、手の上に立てた棒を倒さないようにするには、手をどのように動かせばよいか、という問題です。
Ⅰ(1) 0~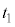 は等加速度運動で、等加速度運動の公式より、
は等加速度運動で、等加速度運動の公式より、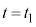 における台車の速度
における台車の速度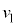 は、
は、 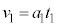 ......[答]
......[答]0~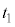 の移動距離
の移動距離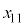 は、
は、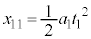
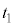 ~
~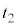 は速度
は速度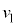 の等速度運動で、移動距離
の等速度運動で、移動距離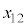 は、
は、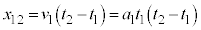
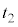 ~
~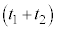 は等加速度運動で、移動距離
は等加速度運動で、移動距離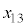 は、
は、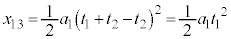 0~
0~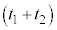 の移動距離は、
の移動距離は、 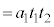 ......[答]
......[答]
物体は、最初に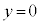 で静止していたのでここが振動端です。単振動の振幅
で静止していたのでここが振動端です。単振動の振幅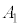 は、
は、 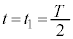 において物体は、単振動の
において物体は、単振動の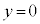 とは逆の振動端、
とは逆の振動端、に来て台車に対して静止します。ここから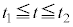 ,つまり、
,つまり、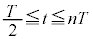 の間は、慣性力がなくなり弾性力のみとなるので、単振動の振動中心は
の間は、慣性力がなくなり弾性力のみとなるので、単振動の振動中心は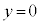 に変わります。
に変わります。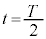 で一旦台車に対して静止するので、ここが振動端となり、振幅
で一旦台車に対して静止するので、ここが振動端となり、振幅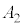 は、
は、 です。物体は、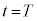 には他の振動端、
には他の振動端、 に来ます。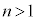 のときは、以降、この単振動が繰り返され、
のときは、以降、この単振動が繰り返され、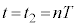 において物体は、
において物体は、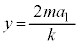 において台車に対して静止します。
において台車に対して静止します。
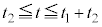 ,つまり、
,つまり、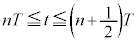 においては、台車の加速度が
においては、台車の加速度が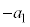 に変わり、物体には慣性力
に変わり、物体には慣性力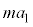 が働きます。単振動の振動中心(
が働きます。単振動の振動中心(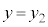 とします)は、
とします)は、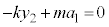 より、
より、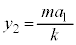
単振動の振幅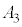 は、
は、 物体は、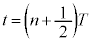 において、もう一つの振動端、
において、もう一つの振動端、 に来ます。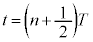 において、物体のy座標は、
において、物体のy座標は、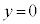 ......[答]この位置で物体は台車に対して静止するので、物体の台車に対する相対速度は、0 ......[答]
......[答]この位置で物体は台車に対して静止するので、物体の台車に対する相対速度は、0 ......[答] 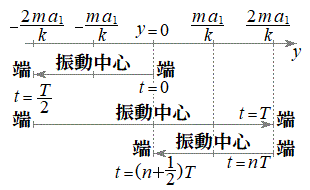 注.上記のように丁寧に考えていくと時間がかかります。試験会場では、右図のような図を描いて、「図より」として効率的に答えるのが賢明です。
注.上記のように丁寧に考えていくと時間がかかります。試験会場では、右図のような図を描いて、「図より」として効率的に答えるのが賢明です。(3) 0~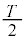 において、台車の加速度が
において、台車の加速度が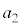 になるので、物体には慣性力
になるので、物体には慣性力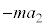 が働き、振動中心
が働き、振動中心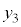 は、
は、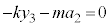 より、
より、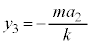 ,振幅
,振幅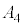 は、
は、
となり、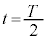 のとき、他の振動端、
のとき、他の振動端、 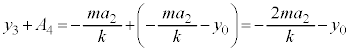 ・・・①
・・・①に来ます。
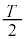 ~Tにおいて、台車の加速度が
~Tにおいて、台車の加速度が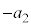 になるので、物体には慣性力
になるので、物体には慣性力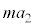 が働き、振動中心
が働き、振動中心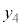 は、
は、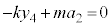 より、
より、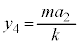 ,振幅
,振幅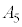 は、
は、 となり、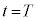 のとき、他の振動端、
のとき、他の振動端、 これが0になるためには、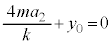 ∴
∴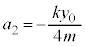 ......[答]
......[答]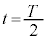 における物体のy座標は、①に代入して、
における物体のy座標は、①に代入して、 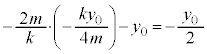 ......[答]
......[答] 注.(3)も(2)と同様に右図のような図を描いて、「図より」として答えるのが賢明です。
注.(3)も(2)と同様に右図のような図を描いて、「図より」として答えるのが賢明です。
Ⅱ(1) 重力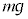 の棒に垂直な成分は
の棒に垂直な成分は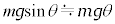 ,慣性力
,慣性力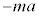 の棒に垂直な成分は、
の棒に垂直な成分は、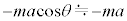 ,よって、質点に働く力の棒に垂直な成分f は、
,よって、質点に働く力の棒に垂直な成分f は、 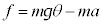 ......[答]
......[答]
(2) 倒立振子は周期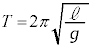 の単振動をします。
の単振動をします。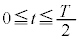 における倒立振子の運動が単振動であることから、図1-3より、振幅は
における倒立振子の運動が単振動であることから、図1-3より、振幅は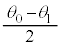 ,振動中心は
,振動中心は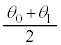 であって、
であって、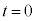 において
において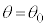 ,
,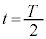 において
において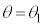 であることより、
であることより、 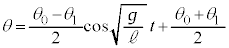 ・・・① [ア] 2 [イ] 1 ......[答]
・・・① [ア] 2 [イ] 1 ......[答]復元力Fは、単振動の角振動数が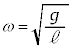 であることから、
であることから、 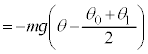 [ウ] 10 ......[答]
[ウ] 10 ......[答]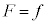 と①より、
と①より、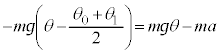
よって、台車の加速度aは、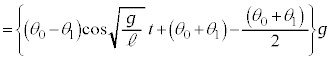
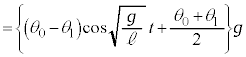 [エ] 4 [オ] 1 ......[答] ・・・②
[エ] 4 [オ] 1 ......[答] ・・・②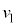 と
と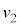 の違いを考えると、単振動の半周期は変わらず、
の違いを考えると、単振動の半周期は変わらず、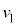 を求める積分のうち、単振動の部分(問題文に書かれている②式の第1項)はやはり0で、図1-3より振動中心は
を求める積分のうち、単振動の部分(問題文に書かれている②式の第1項)はやはり0で、図1-3より振動中心は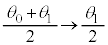 であって、
であって、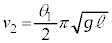 [ii]
[ii] 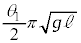 ......[答]
......[答]時刻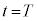 において台車が静止するので、0~Tの台車の速度の変化について、
において台車が静止するので、0~Tの台車の速度の変化について、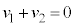 です。よって、[i],[ii]より、
です。よって、[i],[ii]より、 注.上記のように台車の加速度を変化させるとき、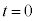 と
と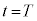 とで、θは0に戻りますが、台車の位置が変化していることに注意してください。Ⅰ(3)でも台車の位置は変化しています。
とで、θは0に戻りますが、台車の位置が変化していることに注意してください。Ⅰ(3)でも台車の位置は変化しています。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 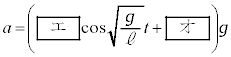
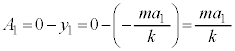
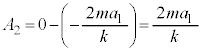
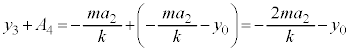 ・・・①
・・・①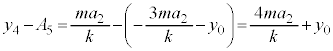
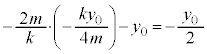 ......[答]
......[答]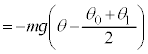 [ウ] 10 ......[答]
[ウ] 10 ......[答]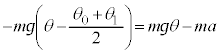
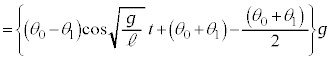
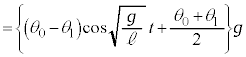 [エ] 4 [オ] 1 ......[答] ・・・②
[エ] 4 [オ] 1 ......[答] ・・・②