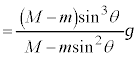�������@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
2�̍��W�nM�CN�������āA����m�̕���P�����W�nM�ɂ����āA��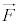 ���������x
���������x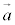 �ʼn^�����Ă����Ƃ���ƁA
�ʼn^�����Ă����Ƃ���ƁA
�@�^���������F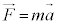 ����@
����@
���W�nM�ɑ��āA���W�nN�͕���P�ƂƂ��ɉ^�����Ă���Ƃ���ƁA���W�nN��ł͕���P�͐Î~���Ċϑ�����邩��A�͂̂荇������������͂��ł���B��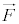 �͑��ς�炸��������A�@�Ɩ������Ȃ����𗧂Ă邽�߂ɂ́A
�͑��ς�炸��������A�@�Ɩ������Ȃ����𗧂Ă邽�߂ɂ́A
�@�͂̂荇���F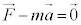 ����A
����A
�ƂȂ�K�v������B���̎��̒��́A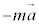 ���������ƌ����B�܂�A�����x
���������ƌ����B�܂�A�����x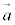 �ʼn^��������W�n��ł́A�����x�Ƌt�����̌���������
�ʼn^��������W�n��ł́A�����x�Ƌt�����̌���������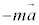 ��������B
��������B
��ʂɁA���W�nM�ɂ����āA����m�̕��̂���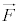 ���������x
���������x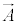 �ʼn^�����Ă����Ƃ���ƁA���W�nM�ɂ����āA
�ʼn^�����Ă����Ƃ���ƁA���W�nM�ɂ����āA
�@�^���������F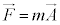
����������B���W�nM�ɑ��������x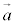 �œ����Ă�����W�nN��ɂ����镨�̂������x��
�œ����Ă�����W�nN��ɂ����镨�̂������x��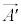 �Ƃ���ƁA�^���������́A
�Ƃ���ƁA�^���������́A
�@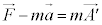
�ɂȂ�B
�͂̂荇�����������Ă���Ƃ��A���̂������x�^�����邩�Î~�𑱂�����W�n(�܂�A�����̖@�������藧���W�n)�������n�ƌ����B����ɑ��āA��������t�������Ȃ���A�����̖@�������藧���Ȃ����W�n�����n�ƌ����B�����n�ɑ��ē����x�^�����Ă�����W�n�͊����n�ł���B
[��1]�@���R�������Ă���F���D(�����x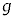 )���ł́A���d�͏���ɂȂ�B����m�̕��̂��F���D���ɂ���Ƃ��āA�d��
)���ł́A���d�͏���ɂȂ�B����m�̕��̂��F���D���ɂ���Ƃ��āA�d��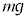 �ȊO�ɁA������
�ȊO�ɁA������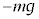 ������āA�͂̂荇���̎��́A
������āA�͂̂荇���̎��́A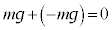 �ƂȂ�B
�ƂȂ�B [��2]�@�����xa�ŏ㏸���Ă���G���x�[�^���ł́A����m�̕��̂ɉ������������d��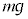 �̑��ɁA������������������
�̑��ɁA������������������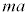 �������A�G���x�[�^�̏�����������R����N�Ƃ���A���̕��̂ɓ����͂̂荇���́A
�������A�G���x�[�^�̏�����������R����N�Ƃ���A���̕��̂ɓ����͂̂荇���́A �ƂȂ�A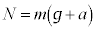 �ƂȂ�܂��B�n�ʂɒu���ꂽ���̂ɓ����d��
�ƂȂ�܂��B�n�ʂɒu���ꂽ���̂ɓ����d��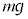 �Ɣ�ׂ�ƁA
�Ɣ�ׂ�ƁA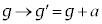 �ƂȂ����悤�Ɍ����܂��B����
�ƂȂ����悤�Ɍ����܂��B����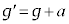 ���������̏d���ƌ����܂��B
���������̏d���ƌ����܂��B [��3]�@�X�pθ �̎Ζʂ�L��������M�̑䂪���炩�ȏ��̏�ɒu����Ă��āA�Ζʏォ������m�̕��̂����ׂ藎�Ƃ��B���̂ƎΖʂ̊Ԃɂ͖��C���Ȃ��Ƃ���B
�Ζʏ�Ō����Ƃ��̕��̂������x�̑傫����a�C��̏��ɑ��������x�̑傫����A�Ƃ���B�Ζʏ�Ō���ƁA���̂ɂ͑�̉^���Ƌt�����ɑ傫��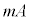 ���������������B�Ζʂ����̂ɋy�ڂ������R����N�Ƃ��āA
���������������B�Ζʂ����̂ɋy�ڂ������R����N�Ƃ��āA
�Ζʏ�Ō����Ƃ��́A�Ζʂɉ��������̕��̂̉^���������F 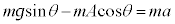 ����@
����@�Ζʏ�Ō����Ƃ��́A�Ζʂɐ����ȕ����̗͂̂肠���F
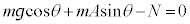 ����A
����A���ʂŌ����Ƃ��́A��̐��������̉^���������F
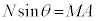 ����B
����B�A���A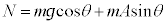
�B�ɑ������ƁA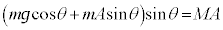
�������āA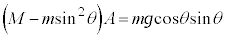
�� 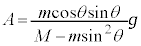 �@�ɑ�����āA
�@�ɑ�����āA �� 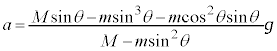
[��4]�@�Î~���������̓V�䂩������l �̂Ђ��ɒ݂邳�ꂽ����m�̂����肪�����P�U��������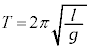 �Ɣ�ׂāA�����xa�Ő��������ɉ^������d�ԓ��œV�䂩������l �̂Ђ��ɒ݂邳�ꂽ�����肪����P�U��������
�Ɣ�ׂāA�����xa�Ő��������ɉ^������d�ԓ��œV�䂩������l �̂Ђ��ɒ݂邳�ꂽ�����肪����P�U��������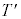 �́A������ɁA�������������d��
�́A������ɁA�������������d��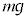 �ɉ����āA����������������
�ɉ����āA����������������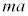 (�����xa�Ƌt������)�������̂ŁA���������d�͉����x
(�����xa�Ƌt������)�������̂ŁA���������d�͉����x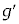 ���A�O�����̒藝�ɂ��A
���A�O�����̒藝�ɂ��A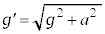 �ƂȂ�A
�ƂȂ�A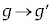 �Ƃ��āA
�Ƃ��āA
�����n�ɂ����ẮA�^���G�l���M�[���ʒu�G�l���M�[�a�́A�͊w�I�G�l���M�[�ۑ����ɂ��ۑ�����܂��B��������n�ōl����ꍇ�ɂ͂ǂ̂悤�ɂȂ�ł��傤��(���n�ɂ����ẮA�͊w�I�G�l���M�[�ۑ��͍l���Ȃ��A�ƕ����Ă���������邩���m��܂���)�H
����M�̕��̂Ƃ��̒��œ�������m�̕��̂���Ȃ�n���l���܂��B����m�̑傫���͍l���܂���BM�ɂ��O��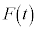 �������AM��m�̊Ԃɂ�����
�������AM��m�̊Ԃɂ�����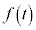 �������AM��m�̑o�����ۑ���
�������AM��m�̑o�����ۑ���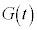 �C
�C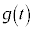 �������Ƃ��܂��B
�������Ƃ��܂��B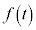 ���o�l���e�����̂悤���ۑ����ł���Ƃ����ꍇ������܂��B
���o�l���e�����̂悤���ۑ����ł���Ƃ����ꍇ������܂��B
M�Cm�������x��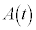 �C
�C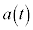 �CM�Cm�����x��
�CM�Cm�����x��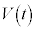 �C
�C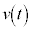 �Ƃ��܂��B
�Ƃ��܂��B
�O�����猩��M���^���������́A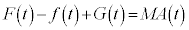 �@����C
�@����C
�O�����猩��m�̉^���������́A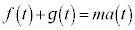 �@����D
�@����D
����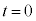 ��������
��������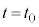 �̊ԂɁA��
�̊ԂɁA��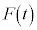 ��M�ɑ��Ă����d��W�́A
��M�ɑ��Ă����d��W�́A
�C���A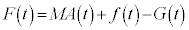 �C������A
�C������A
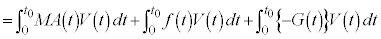 �@����E
�@����E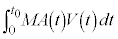 �́A
�́A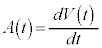 �C
�C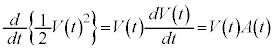 (�������̔����@���Q��)���A
(�������̔����@���Q��)���A
�́A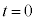 ����
����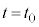 �̊Ԃ�M�������^���G�l���M�[�̑����ł��B
�̊Ԃ�M�������^���G�l���M�[�̑����ł��B
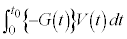 �́A�ۑ���
�́A�ۑ���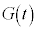 �ɋt�炤�O��
�ɋt�炤�O��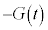 ��M�ɂ����d���ŁA�ۑ���
��M�ɂ����d���ŁA�ۑ���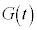 �ɂ��M���ʒu�G�l���M�[�̑���
�ɂ��M���ʒu�G�l���M�[�̑���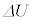 �ł��B
�ł��B
�c��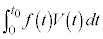 �ɂ��āA�ׂ������ׂĂ݂܂��B
�ɂ��āA�ׂ������ׂĂ݂܂��B
����M���畨��m�̉^�������āA����m�����Ή����x��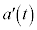 �C���Α��x��
�C���Α��x��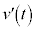 �Ƃ��܂��B
�Ƃ��܂��B
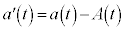 �C
�C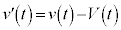 �@����F
�@����F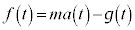 �C����ƇF��p����ƁA
�C����ƇF��p����ƁA
���̂�����1���A��2���̐ϕ��́A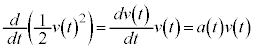 �C
�C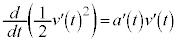 ���A��3���̐ϕ������āA
���A��3���̐ϕ������āA
�G�̑�4���̐ϕ��́A�F��p���āA
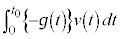 �́A
�́A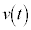 �������Đϕ����Ă���̂ŁA�O�����猩���Ƃ����ۑ���
�������Đϕ����Ă���̂ŁA�O�����猩���Ƃ����ۑ���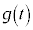 �ɋt�炤�O��
�ɋt�炤�O��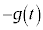 �̂����d���A�܂�A�O�����猩�������ۑ���
�̂����d���A�܂�A�O�����猩�������ۑ���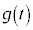 �ɂ���ʒu�G�l���M�[�̑���
�ɂ���ʒu�G�l���M�[�̑���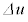 �ł��B
�ł��B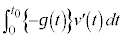 �́A
�́A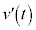 �������Đϕ����Ă���̂ŁA����M���猩���Ƃ����ۑ���
�������Đϕ����Ă���̂ŁA����M���猩���Ƃ����ۑ���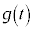 �ɂ���ʒu�G�l���M�[�̑���
�ɂ���ʒu�G�l���M�[�̑���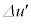 �ł��B
�ł��B
����W�C�����E�́A
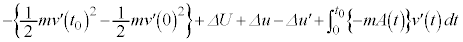 �@����H
�@����H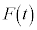 ��M�ɑ��Ă����d���́AM���^���G�l���M�[�̑���
��M�ɑ��Ă����d���́AM���^���G�l���M�[�̑���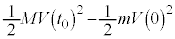 �C�O�����猩��m���^���G�l���M�[�̑���
�C�O�����猩��m���^���G�l���M�[�̑���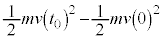 �ƁA�O�����猩��M�Cm���ʒu�G�l���M�[�̑���
�ƁA�O�����猩��M�Cm���ʒu�G�l���M�[�̑���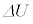 �C
�C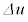 �̑��a�ɂȂ�܂��B�܂�A
�̑��a�ɂȂ�܂��B�܂�A
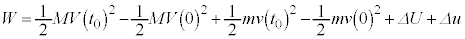 �@����I
�@����I
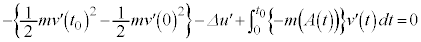 �@����J
�@����J
���āA�D���ɁA�F��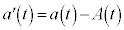 ���
���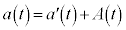 ��������ƁA
��������ƁA
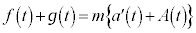
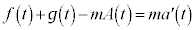 �@����K
�@����K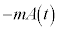 �͕���M�������x�Ƌt�������������ł��B����M���猩�āA����M���^���G�l���M�[�͂���܂���B����M���猩�āA����m���^���G�l���M�[�̑����́A
�͕���M�������x�Ƌt�������������ł��B����M���猩�āA����M���^���G�l���M�[�͂���܂���B����M���猩�āA����m���^���G�l���M�[�̑����́A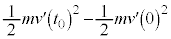 �ł��B
�ł��B
����M���猩������m���ʒu�G�l���M�[�̑����́A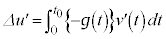 �ł��B
�ł��B
����M���猩�āA�������̂����d���́A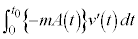 �ł��B
�ł��B
����ƁA����M���猩���͊w�I�G�l���M�[�ۑ��́A
�ƂȂ�܂����A�J���Ɉ�v���܂��B����́A���n�ɂ����āA���������d�����l���ɓ���ė͊w�I�G�l���M�[�ۑ����l����A��n�ɂ�����͊w�I�G�l���M�[�ۑ��Ɩ������Ȃ����Ƃ��Ӗ����Ă��܂��B
���n�ɂ����āA���������l���ɓ���ė͊w�I�G�l���M�[�ۑ�����K�p�ł������ȉ��̃����N��Ŏ����܂��B
���n�ɂ�����͊w�I�G�l���M�[�ۑ����Q�Ƃ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B