������w2021�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
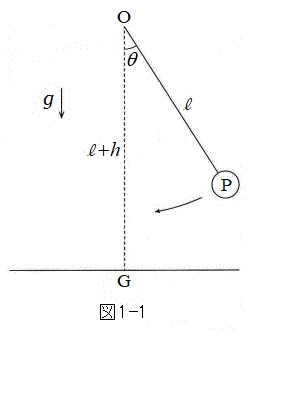 [1]�@�}1-1�Ɏ����悤�ȃu�����R�̉^���ɂ��čl���Ă݂悤�B�u�����R�̎x�_��O�Ƃ���B�u�����R�ɏ���Ă���l������m�̎��_�Ƃ݂Ȃ��A���_P�ƌĂԂ��Ƃɂ���B�x�_O���琅���Ȓn�ʂɂ��낵�������̑���G�Ƃ���B�u�����R�̒���OP��
[1]�@�}1-1�Ɏ����悤�ȃu�����R�̉^���ɂ��čl���Ă݂悤�B�u�����R�̎x�_��O�Ƃ���B�u�����R�ɏ���Ă���l������m�̎��_�Ƃ݂Ȃ��A���_P�ƌĂԂ��Ƃɂ���B�x�_O���琅���Ȓn�ʂɂ��낵�������̑���G�Ƃ���B�u�����R�̒���OP��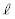 �C�x�_O�̍���OG��
�C�x�_O�̍���OG��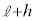 �Ƃ���B�u�����R�̐U��p
�Ƃ���B�u�����R�̐U��p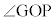 ��θ�Ƃ��Aθ��OG����ɔ����v���𐳂ɂƂ�B�d�͉����x�̑傫����
��θ�Ƃ��Aθ��OG����ɔ����v���𐳂ɂƂ�B�d�͉����x�̑傫����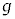 �Ƃ���B�܂��A�u�����R�͎��ʓ��݂̂ł���ނ��ƂȂ��^��������̂Ƃ��A�u�����R�̎��ʂ▀�C�A��C��R�͖�������B
�Ƃ���B�܂��A�u�����R�͎��ʓ��݂̂ł���ނ��ƂȂ��^��������̂Ƃ��A�u�����R�̎��ʂ▀�C�A��C��R�͖�������B
�T�@�ȉ��̕��͂��@�A�@�`�@�E�@�ɂ��Ă͂܂鎮���A���ꂼ�꒼��̊��ʓ��̕�����p���ĕ\���B
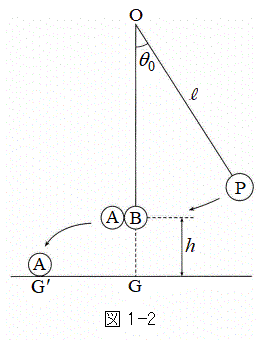
�U�@�u�����R�ɓ�l��������ꍇ���l���悤�B����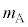 �̎��_A�ƁA����
�̎��_A�ƁA����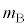 �̎��_B���l����B�}1-2�Ɏ����悤�ɁA������Ԃł�A��B�����킳���Ď��_P���Ȃ��Ă���Ƃ��A���_P��
�̎��_B���l����B�}1-2�Ɏ����悤�ɁA������Ԃł�A��B�����킳���Ď��_P���Ȃ��Ă���Ƃ��A���_P��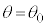 ����Â��ɉ^�����n�߂��Ƃ���B
����Â��ɉ^�����n�߂��Ƃ���B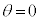 �ɂ�����A�̓u�����R���э~��A����
�ɂ�����A�̓u�����R���э~��A����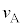 �Ő����ɉ^�����n�߂��B����AA����э~�肽���Ƃɂ��AB���悹���u�����R��
�Ő����ɉ^�����n�߂��B����AA����э~�肽���Ƃɂ��AB���悹���u�����R��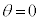 �ł��̂܂ܐÎ~�����B���̌�A��
�ł��̂܂ܐÎ~�����B���̌�A��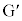 �ɒ��n�����B
�ɒ��n�����B
(1) A����э~��钼�O�̎��_P�̑�����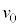 �Ƃ��āA
�Ƃ��āA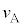 ��
��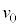 �C
�C �C
�C ��p���ĕ\���B
��p���ĕ\���B
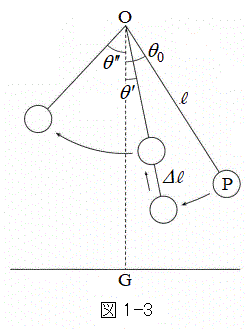
�V�@�u�����R���������Ƃ��l���悤�B�u�����R�ɏ�����l���^���̓r���ŗ����オ�����肵�Ⴊ�݂��肷�邱�ƂŁA�u�����R�̐U�ꕝ���ω����Ă����B
�܂��}1-3�Ɏ����悤�ɁA�l���u�����R�ň�x���������オ�邱�Ƃ��ȉ��̂悤�ɍl����B����m�̎��_P�� (
(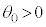 )����Â��ɉ^�����n�߂��B���Ɋp�x
)����Â��ɉ^�����n�߂��B���Ɋp�x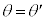 �ɂ����Đl�������オ�������Ƃɂ��AOP�̒�����
�ɂ����Đl�������オ�������Ƃɂ��AOP�̒�����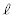 ����
����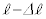 �ւƏu���ɕω������Ƃ���(
�ւƏu���ɕω������Ƃ���(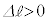 )�BOP�̒������ω����钼�O��P�̑�����v�Ƃ��A����̑�����
)�BOP�̒������ω����钼�O��P�̑�����v�Ƃ��A����̑�����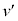 �Ƃ���B���̌�AOP�̒�����
�Ƃ���B���̌�AOP�̒�����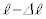 �̂܂�P�͉^���𑱂��A�p�x
�̂܂�P�͉^���𑱂��A�p�x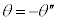 (
(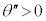 )�ŐÎ~�����B�������ȉ��ł́A�u�����R�̐U��pθ�͏�ɏ\���������Ƃ��āA
)�ŐÎ~�����B�������ȉ��ł́A�u�����R�̐U��pθ�͏�ɏ\���������Ƃ��āA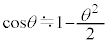 �Ƌߎ��ł��邱�Ƃ�p����B
�Ƌߎ��ł��邱�Ƃ�p����B
(1) 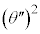 ��
��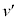 �C
�C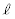 �C
�C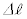 �C
�C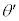 �C
�C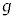 ��p���ĕ\���B
��p���ĕ\���B OP�̒������ω�����O��Ɋւ��Ĉȉ��̂悤�ɍl���邱�Ƃ��ł���B����OP�̕ω����\��������A�u�ԓI��OP�����̋����͂��������ƍl������BO�𒆐S�Ƃ������W�n�ōl����ƁA���̗͂͒��S�͂Ȃ̂ŁA�ʐϑ��x������OP�̕ω��̑O��ň��ł���Ƃ��Ă悢�B�܂�A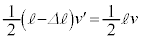 �����藧�B
�����藧�B
(3) 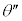 ���ő�ɂ���
���ő�ɂ���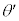 �ƁA���̎���
�ƁA���̎���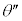 ��
��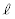 �C
�C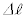 �C
�C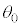 ��p���ĕ\���B
��p���ĕ\���B ���ɁA�l�����x�������オ�����肵�Ⴊ�݂��肵�ău�����R���������Ƃ��A�ȉ��̂悤�ȃT�C�N���Ƃ��čl���Ă݂悤�Bn��ڂ̃T�C�N��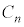 (
(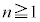 )�����̂悤�ɒ�`����B
)�����̂悤�ɒ�`����B �u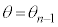 �ŐÎ~�������_P��OP�̒���
�ŐÎ~�������_P��OP�̒���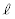 �ŐÂ��ɉ^�����J�n����B
�ŐÂ��ɉ^�����J�n����B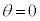 �ɂ����ė����オ��OP�̒�����
�ɂ����ė����オ��OP�̒�����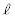 ����
����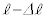 �ւƏu���ɕω�����B���_P��OP�̒���
�ւƏu���ɕω�����B���_P��OP�̒���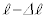 �̂܂܊p�x
�̂܂܊p�x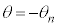 �ŐÎ~������A�t�����ɉ^�����n�߁A�p�x
�ŐÎ~������A�t�����ɉ^�����n�߁A�p�x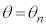 �ōĂѐÎ~����B���̂Ƃ��A
�ōĂѐÎ~����B���̂Ƃ��A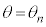 �ł��Ⴊ�݂��݁AOP�̒�����
�ł��Ⴊ�݂��݁AOP�̒�����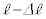 ����Ă�
����Ă�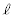 �ւƏu���ɕω�����B�v
�ւƏu���ɕω�����B�v 1��ڂ̃T�C�N�����n�߂�O�A���_P��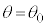 (
(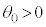 )�ɂ���AOP�̒�����
)�ɂ���AOP�̒�����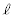 �������B���̌�A�T�C�N��
�������B���̌�A�T�C�N��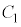 ���J�n���A�ȉ�����
���J�n���A�ȉ�����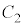 �C
�C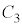 �C����Ɖ^���𑱂��Ă������̂Ƃ���B
�C����Ɖ^���𑱂��Ă������̂Ƃ���B
(4) n��ڂ̃T�C�N���̌�̃u�����R�̊p�x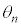 ���A
���A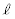 �C
�C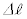 �C
�C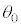 �Cn��p���ĕ\���B
�Cn��p���ĕ\���B
(5) 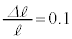 �̂Ƃ��AN��ڂ̃T�C�N���̌�ɁA���߂�
�̂Ƃ��AN��ڂ̃T�C�N���̌�ɁA���߂�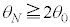 �ƂȂ����BN�����߂�B�������A
�ƂȂ����BN�����߂�B�������A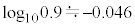 �C�����
�C�����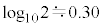 �ł��邱�Ƃ�p���Ă��悢�B
�ł��邱�Ƃ�p���Ă��悢�B
[��]
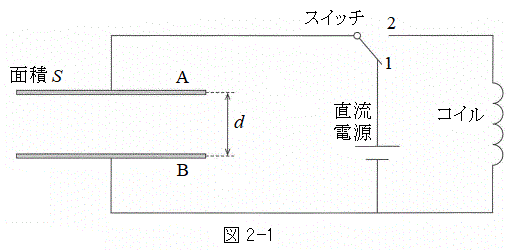 [2]�@�ʐ�S�̌��݂̖����ł�������̔�A�Ɣ�B����C���ŋ���d���������ĕ��s�ɔz�u�����Bd�͏\���ɏ������A�̒[�̌��ʂ͖�������B�}2-1�̂悤�ɁA�A�X�C�b�`�A�����d���A�R�C�����łȂ����B�����d���̓�����R�⓱���̒�R�͖����ł���قǏ������B��C�̗U�d����ε�Ƃ���B
[2]�@�ʐ�S�̌��݂̖����ł�������̔�A�Ɣ�B����C���ŋ���d���������ĕ��s�ɔz�u�����Bd�͏\���ɏ������A�̒[�̌��ʂ͖�������B�}2-1�̂悤�ɁA�A�X�C�b�`�A�����d���A�R�C�����łȂ����B�����d���̓�����R�⓱���̒�R�͖����ł���قǏ������B��C�̗U�d����ε�Ƃ���B
�T�@�}2-1�̂悤�ɁA�X�C�b�`��1�ɂȂ��A��A�Ɣ�B�̊Ԃɒ����d��V (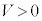 )���������Ƃ���A��A�CB�ɂ��ꂼ��d��Q�C
)���������Ƃ���A��A�CB�ɂ��ꂼ��d��Q�C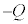 ���~�����A
���~�����A �̊W�����邱�Ƃ����������B
�̊W�����邱�Ƃ����������B
(1) 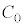 ��S�Cd�Cε��p���ĕ\���B
��S�Cd�Cε��p���ĕ\���B 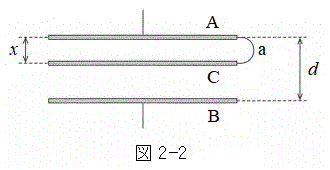 (2) ��A�CB�Ɠ����`������ʐ�S�̌��݂̖����ł�������̔�C��}2-2�̂悤�ɔ�A�Ɣ�B�̊ԂɌ݂��ɕ��s�ɂȂ�悤�ɍ������ꂽ�B��A�Ɣ�C�̋�����x (
(2) ��A�CB�Ɠ����`������ʐ�S�̌��݂̖����ł�������̔�C��}2-2�̂悤�ɔ�A�Ɣ�B�̊ԂɌ݂��ɕ��s�ɂȂ�悤�ɍ������ꂽ�B��A�Ɣ�C�̋�����x (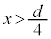 )�ł���B����ɁA��A�Ɣ�C���̖����ł��铱��a�Őڑ����A�\�����Ԃ��o�߂����Ƃ���A��A�CC�CB�ɒ~����ꂽ�d�ׂ͂��ꂼ����ƂȂ����B��A�CC�CB����Ȃ�R���f���T�[�ɒ~����ꂽ�Ód�G�l���M�[�����߂�B
)�ł���B����ɁA��A�Ɣ�C���̖����ł��铱��a�Őڑ����A�\�����Ԃ��o�߂����Ƃ���A��A�CC�CB�ɒ~����ꂽ�d�ׂ͂��ꂼ����ƂȂ����B��A�CC�CB����Ȃ�R���f���T�[�ɒ~����ꂽ�Ód�G�l���M�[�����߂�B
(3) �O�͂������A��C���������Ɣ�A�ɋ߂Â��Ĕ�A�Ɣ�C�̋�����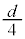 �ɂ����B����a�͂��炩���A��C�������߂̗͂ɂ͉e�����Ȃ��Ƃ���B��C�ɊO�͂������d��W�����߂�B�܂��AW�͓d���������d��
�ɂ����B����a�͂��炩���A��C�������߂̗͂ɂ͉e�����Ȃ��Ƃ���B��C�ɊO�͂������d��W�����߂�B�܂��AW�͓d���������d��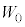 �̉��{�ł��邩�����̕������܂߂ē�����B
�̉��{�ł��邩�����̕������܂߂ē�����B
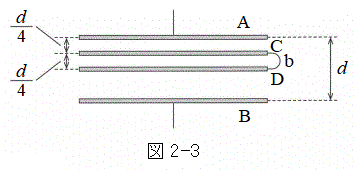 �U�@�ݖ�T(3)�̏�Ԃ���A��A�CB�CC�Ɠ����`������ʐ�S�̌��݂̖����ł�������̔�D���A��C�Ɣ�B�̊ԂɌ݂��ɕ��s�ɂȂ�悤�ɍ������ꂽ�B��C�Ɣ�D�̋�����
�U�@�ݖ�T(3)�̏�Ԃ���A��A�CB�CC�Ɠ����`������ʐ�S�̌��݂̖����ł�������̔�D���A��C�Ɣ�B�̊ԂɌ݂��ɕ��s�ɂȂ�悤�ɍ������ꂽ�B��C�Ɣ�D�̋�����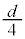 �ł���B����ɁA��C�Ɣ�D���̖����ł��铱��b�Őڑ������B�\�����Ԃ��o�߂��Ċe�ɒ~����ꂽ�d�ׂ����ꂼ����ƂȂ�����ɁA�}2-3�̂悤�ɓ���a���O�����B
�ł���B����ɁA��C�Ɣ�D���̖����ł��铱��b�Őڑ������B�\�����Ԃ��o�߂��Ċe�ɒ~����ꂽ�d�ׂ����ꂼ����ƂȂ�����ɁA�}2-3�̂悤�ɓ���a���O�����B
(1) ��A�ɒ~����ꂽ�d�ׂ� �C��B�ɒ~����ꂽ�d�ׂ�
�C��B�ɒ~����ꂽ�d�ׂ�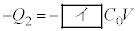 �ƕ\�����B
�ƕ\�����B �C
�C �ɓ��鐔����B
�ɓ��鐔����B
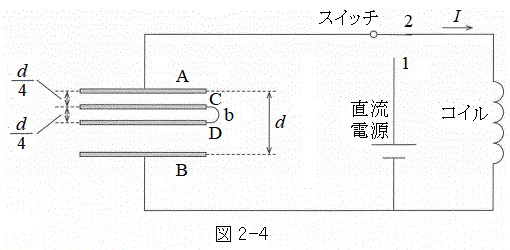
�V�@�ݖ�U(2)�̏�Ԃ���A���� �Ő}2-4�̂悤�ɃX�C�b�`��1����2�ɂȂ��������Ƃ���A�R�C���ɂ�
�Ő}2-4�̂悤�ɃX�C�b�`��1����2�ɂȂ��������Ƃ���A�R�C���ɂ�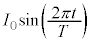 �ƕ\�����d��I������邱�Ƃ����������B�������A�}���̖��̌�����d���̐��̌����ɂƂ�B�R�C���̒�R�͖����ł��A���ȃC���_�N�^���X��L�ł���B���ɐ������Ȃ��ꍇ�́A�����d���̓d����
�ƕ\�����d��I������邱�Ƃ����������B�������A�}���̖��̌�����d���̐��̌����ɂƂ�B�R�C���̒�R�͖����ł��A���ȃC���_�N�^���X��L�ł���B���ɐ������Ȃ��ꍇ�́A�����d���̓d����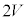 �Ƃ���B
�Ƃ���B
(1) T��L��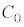 ��p���ĕ\���B
��p���ĕ\���B
(2) 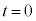 �ŃR�C���̗��[�ɂ�����d������B�܂��A
�ŃR�C���̗��[�ɂ�����d������B�܂��A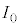 ��T�CV�CL��p���ĕ\���B�������A��������
��T�CV�CL��p���ĕ\���B�������A��������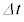 �̊Ԃ̓d���ω���
�̊Ԃ̓d���ω���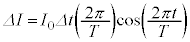 �ł��邱�Ƃ�p���Ă悢�B
�ł��邱�Ƃ�p���Ă悢�B
(3) ��A�CB�̓d�ׂ����ꂼ��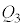 �C
�C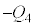 �Ƃ���ƁA
�Ƃ���ƁA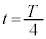 �̂Ƃ�
�̂Ƃ� �̊W�����藧�B
�̊W�����藧�B �ɓ��鐔����B�܂��A
�ɓ��鐔����B�܂��A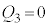 �ƂȂ鎞��
�ƂȂ鎞��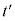 ��T��p���ĕ\���B������
��T��p���ĕ\���B������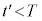 �Ƃ���B
�Ƃ���B
(4) ��A�CC�CD�CB����Ȃ�R���f���T�[�ɒ~������Ód�G�l���M�[���A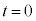 �̂Ƃ���
�̂Ƃ���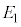 �C
�C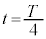 �̂Ƃ���
�̂Ƃ���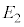 �ł������B
�ł������B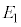 �C
�C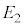 �����ꂼ��
�����ꂼ��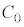 �CV��p���ĕ\���B�܂��A
�CV��p���ĕ\���B�܂��A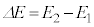 �Ƃ��āA
�Ƃ��āA ��
�� ���܂݁AV�����T���܂܂Ȃ��`�ŕ\���B
���܂݁AV�����T���܂܂Ȃ��`�ŕ\���B  �����d���̓d����
�����d���̓d����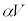 (
(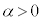 )�ł������ꍇ���l����B
)�ł������ꍇ���l����B
(5) ����α�ɑ��āA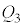 ��
��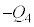 �̕ω��̗l�q��\���ł��K�Ȑ}��}2-5�̇@�`�E����I�сA�ԍ��œ�����B�}���œ_����
�̕ω��̗l�q��\���ł��K�Ȑ}��}2-5�̇@�`�E����I�сA�ԍ��œ�����B�}���œ_����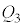 ��\���A������
��\���A������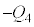 ��\���B
��\���B
[��]
[3]�@2018�N�̃m�[�x�������w�܂́A�u���[�U�[�����w����ɂ��������I�Ȕ����v�ɑ��Ď��^����A���̂�����1�͌��s���Z�b�g�Z�p�Ɋւ�����̂ł������B���s���Z�b�g�Ƃ́A���[�U�[���Ŕ����ȗ��q����ߑ�����Z�p�ł���B�{��ł́A���������q�ɋy�ڂ��͂��l�@���邱�ƂŁA���Ŕ����q���ߑ��ł��邱�Ƃ��m�F���Ă݂悤�B
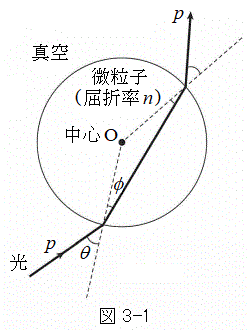 �ȉ��A�}3-1�ɗ�������悤�ɁA�^�ɋ��ܗ�n (
�ȉ��A�}3-1�ɗ�������悤�ɁA�^�ɋ��ܗ�n (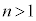 )�̋��`�̔����q������A�������������ʉ߂�����l����B���͌��q�Ƃ������q�̏W�܂�̗���ł���A���q�͉^���ʂ����̂ŁA���̋��܂ɔ������q�̉^���ʂ��ω����āA���ꂪ�����q�ɗ͂��y�ڂ��ƍl������B�����ňȉ��ł́A���q�̉^���ʂ̕ω��̑傫���́A���̌��q�������q�ɋy�ڂ��͐ς̑傫���ɓ������Ƃ���B�܂��A���̋z���┽�˂̉e���͖�������B����ɁA�����q�ɑ��Č����͏\���ɍׂ��A�����̑����͍l���Ȃ��B
)�̋��`�̔����q������A�������������ʉ߂�����l����B���͌��q�Ƃ������q�̏W�܂�̗���ł���A���q�͉^���ʂ����̂ŁA���̋��܂ɔ������q�̉^���ʂ��ω����āA���ꂪ�����q�ɗ͂��y�ڂ��ƍl������B�����ňȉ��ł́A���q�̉^���ʂ̕ω��̑傫���́A���̌��q�������q�ɋy�ڂ��͐ς̑傫���ɓ������Ƃ���B�܂��A���̋z���┽�˂̉e���͖�������B����ɁA�����q�ɑ��Č����͏\���ɍׂ��A�����̑����͍l���Ȃ��B
�T�@�}3-1�Ɏ����悤�ɁA�^�̔����q���������ʉ߂��Ă���B�����q�̒��SO�͌����Ɠ��ꕽ�ʓ��ɂ���B�����q�͌Œ肳��Ă���A�����Ȃ��B�}3-2�Ɏ����悤�ɁA�����������q�ɓ��˂���_��_A�C�����q����ˏo����_��_B�Ƃ���B���ˑO�̌������������������ƁA�ˏo��̌������������������̌�_��_C�Ƃ���B����AB�Ɛ���OC�̌�_��_D�Ƃ���B�ȉ��̐ݖ�ɓ�����B (1) ���������q�ɓ��˂���ۂ̓��ˊp��θ�C���܊p��ϕ�Ƃ���B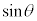 ���An�C
���An�C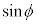 ��p���ĕ\���B
��p���ĕ\���B
(2) �������������ɗ������q�̏W�܂肪���A�G�l���M�[�̑���E�Ɖ^���ʂ̑傫���̑���p�̊Ԃɂ́A�^�ł�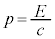 �Ƃ����W�����藧�B�����ŁAc�͐^�̌��̑����ł���B�}3-1�̌��́A�P�ʎ��Ԃ�����Q�̃G�l���M�[�������āA��������ˏo����Ă���B���̂Ƃ��A����
�Ƃ����W�����藧�B�����ŁAc�͐^�̌��̑����ł���B�}3-1�̌��́A�P�ʎ��Ԃ�����Q�̃G�l���M�[�������āA��������ˏo����Ă���B���̂Ƃ��A����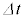 �̊ԂɎˏo���ꂽ���q�̏W�܂肪�^�ł��^���ʂ̑傫���̑���p���AQ�C
�̊ԂɎˏo���ꂽ���q�̏W�܂肪�^�ł��^���ʂ̑傫���̑���p���AQ�C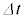 �Cc�Cn�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cc�Cn�̂����K�v�Ȃ��̂�p���ĕ\���B
(3) �}3-1�Ɏ����悤�ɁA�����q�ɓ��˂���O�̌��q�ƁA�����q����ˏo�������q�́A�^���ʂ̑傫���͕ς��Ȃ����A�����͕ω����Ă���B����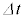 �̊ԂɎˏo���ꂽ���q�̏W�܂肪�A�����q��ʉ߂��邱�Ƃɂ���^���ʂ̕ω��̑傫���̑���
�̊ԂɎˏo���ꂽ���q�̏W�܂肪�A�����q��ʉ߂��邱�Ƃɂ���^���ʂ̕ω��̑傫���̑���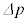 ���Ap�Cθ�Cϕ��p���ĕ\���B�܂��A���̌������A�_O�CA�CB�CC�̂����K�v�Ȃ��̂�p���ĕ\���B
���Ap�Cθ�Cϕ��p���ĕ\���B�܂��A���̌������A�_O�CA�CB�CC�̂����K�v�Ȃ��̂�p���ĕ\���B
(4) ���̔����q���������͂̑傫��f ���AQ�Cc�Cθ�Cϕ�̂����K�v�Ȃ��̂�p���ĕ\���B�܂��A���̌������A�_O�CA�CB�CC�̂����K�v�Ȃ��̂�p���ĕ\���B
(5) �}3-2�Ɏ����悤�ɁAOD�Ԃ̋�����d�C�����q�̔��a��r�Ƃ���B�p�xθ�Cϕ���������Ƃ��A�ݖ�T(4)�ŋ��߂��͂̑傫��f ���AQ�Cc�Cn�Cr�Cd�̂����K�v�Ȃ��̂�p���ĕ\���B�����Ȋp�xδ�ɑ��Đ��藧�ߎ���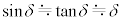 �C
�C ���g���A�ŏI���ʂɂ͎O�p�����܂߂��ɉ��邱�ƁB
���g���A�ŏI���ʂɂ͎O�p�����܂߂��ɉ��邱�ƁB
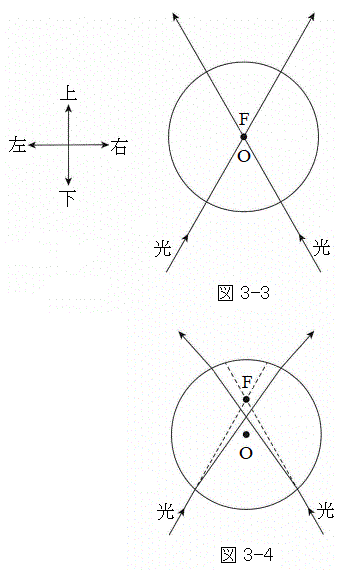 �U�@�}3-3�C�}3-4�Ɏ����悤�ɁA���x(�P�ʎ��Ԃ�����̃G�l���M�[)�̓�����2�{�̌������_F�Ō����悤���H�����������ŁA�ݖ�T�Ɠ��������q���A���ꂼ��قȂ�ʒu�ɒu�����B������̐}�ɂ����Ă��A���ˌ���������(�㉺����)�ƂȂ��p�x��2�{�̌����œ������A2�{�̌����Ɣ����q�̒��SO�͓��ꕽ�ʓ��ɂ���B�����q�͌Œ肳��Ă���A�����Ȃ��B�ȉ��̐ݖ�ɓ�����B�͂̌����ɂ��ẮA�ݖ�̎w���ɏ]���āA�͂������ꍇ�͐}3-3�̍����ɐ}�������㉺���E�̂����ꂩ�����A�͂������Ȃ��ꍇ�́u�͓͂����Ȃ��v�Ɠ����邱�ƁB
�U�@�}3-3�C�}3-4�Ɏ����悤�ɁA���x(�P�ʎ��Ԃ�����̃G�l���M�[)�̓�����2�{�̌������_F�Ō����悤���H�����������ŁA�ݖ�T�Ɠ��������q���A���ꂼ��قȂ�ʒu�ɒu�����B������̐}�ɂ����Ă��A���ˌ���������(�㉺����)�ƂȂ��p�x��2�{�̌����œ������A2�{�̌����Ɣ����q�̒��SO�͓��ꕽ�ʓ��ɂ���B�����q�͌Œ肳��Ă���A�����Ȃ��B�ȉ��̐ݖ�ɓ�����B�͂̌����ɂ��ẮA�ݖ�̎w���ɏ]���āA�͂������ꍇ�͐}3-3�̍����ɐ}�������㉺���E�̂����ꂩ�����A�͂������Ȃ��ꍇ�́u�͓͂����Ȃ��v�Ɠ����邱�ƁB
(1) �}3-3�Ɏ����悤�ɁA�����q�̒��SO���_F�ƈ�v���Ă���Ƃ��A�����q��2�{�̌�����鍇�͂̌����Ƃ��čł��K�Ȃ��̂��u��v�u���v�u���v�u�E�v�u�͓͂����Ȃ��v����I������B
(2) �}3-4�Ɏ����悤�ɁA�����q�̒��SO���_F�̉��ɂ���Ƃ��A�����q��2�{�̌�����鍇�͂̌����Ƃ��čł��K�Ȃ��̂��u��v�u���v�u���v�u�E�v�u�͓͂����Ȃ��v����I������B�_F�͔����q�̓����ɂ���AOF�Ԃ̋����͏\�����������̂Ƃ���B
(3) �ݖ�U(2)�ɂ����āAOF�Ԃ̋�����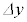 �Ƃ���Ƃ��A�����q��2�{�̌�����鍇�͂̑傫��
�Ƃ���Ƃ��A�����q��2�{�̌�����鍇�͂̑傫��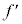 ��
��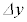 �̊Ԃ̊W�ɂ��āA�ł��K�Ȃ��̂��ȉ��̃A�`�G����I������B�Ȃ��A�����q�̔��ar�Ɣ�ׂ�
�̊Ԃ̊W�ɂ��āA�ł��K�Ȃ��̂��ȉ��̃A�`�G����I������B�Ȃ��A�����q�̔��ar�Ɣ�ׂ�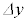 �͏������A�ݖ�T(5)�̋ߎ����{�ݖ�ł��L���ł���B�}3-4�́A
�͏������A�ݖ�T(5)�̋ߎ����{�ݖ�ł��L���ł���B�}3-4�́A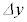 �̑傫�����֒����ĕ`����Ă���̂Œ��ӂ��邱�ƁB
�̑傫�����֒����ĕ`����Ă���̂Œ��ӂ��邱�ƁB �A�F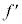 ��
��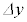 �ɂ�炸���ł���B
�ɂ�炸���ł���B �C�F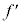 ��
��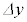 �ɔ�Ⴗ��B
�ɔ�Ⴗ��B �E�F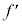 ��
��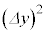 �ɔ�Ⴗ��B
�ɔ�Ⴗ��B �G�F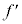 ��
��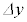 �ɔ���Ⴗ��B
�ɔ���Ⴗ��B
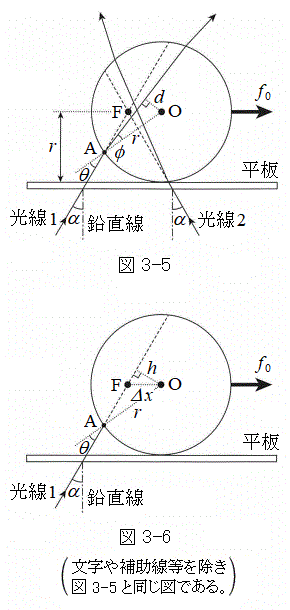 �V�@�}3-5�Ɏ����悤�ɁA�����ɒu���ꂽ���������ȕ��̏���A����r�̈ʒu�ɂ���_F�ŁA���x�̓�����2�{�̌���(����1�C����2)�������悤���H�����������ŁA�ݖ�T�C�ݖ�U�Ɠ����A���ar�̔����q��u�����B�����q�͏�ɕ��ƐڐG���Ă���A�����q�ƕ��̊Ԃɖ��C�͂Ȃ����̂Ƃ���B�����q�ɂ́A�O������E�����ɑ傫��
�V�@�}3-5�Ɏ����悤�ɁA�����ɒu���ꂽ���������ȕ��̏���A����r�̈ʒu�ɂ���_F�ŁA���x�̓�����2�{�̌���(����1�C����2)�������悤���H�����������ŁA�ݖ�T�C�ݖ�U�Ɠ����A���ar�̔����q��u�����B�����q�͏�ɕ��ƐڐG���Ă���A�����q�ƕ��̊Ԃɖ��C�͂Ȃ����̂Ƃ���B�����q�ɂ́A�O������E�����ɑ傫��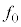 �̗͂������Ă���A���̗͂ƁA2�{�̌��������͂��ނ荇���ʒu�Ŕ����q�͐Î~���Ă���B���Ȃ킿�A���̔����q�́A���ɂ���ĕߑ�����Ă���BOF�Ԃ̋�����
�̗͂������Ă���A���̗͂ƁA2�{�̌��������͂��ނ荇���ʒu�Ŕ����q�͐Î~���Ă���B���Ȃ킿�A���̔����q�́A���ɂ���ĕߑ�����Ă���BOF�Ԃ̋�����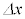 �Ƃ��A�_F�́A�����q�̓����A���SO�t�߂ɂ���B�܂��A���ˌ����������ƂȂ��p�xα��2�{�̌����œ������A2�{�̌����Ɠ_O�͓��ꕽ�ʓ��ɂ���B���͏\���ɔ����A���ɂ����̋��܂┽�ˁA�z���͍l���Ȃ��B���������q�ɓ��˂���ۂ̓��ˊpθ��2�{�̌����œ������A����ɑ�����܊p��ϕ�Ƃ���B�����q�╽�̕ό`�͍l���Ȃ��B
�Ƃ��A�_F�́A�����q�̓����A���SO�t�߂ɂ���B�܂��A���ˌ����������ƂȂ��p�xα��2�{�̌����œ������A2�{�̌����Ɠ_O�͓��ꕽ�ʓ��ɂ���B���͏\���ɔ����A���ɂ����̋��܂┽�ˁA�z���͍l���Ȃ��B���������q�ɓ��˂���ۂ̓��ˊpθ��2�{�̌����œ������A����ɑ�����܊p��ϕ�Ƃ���B�����q�╽�̕ό`�͍l���Ȃ��B
(1) �}3-5�Ɏ����悤�ɁA����1�������q�ɓ��˂���_��_A�Ƃ��A�����q�̒��SO��������q���̌���1�̏�ɍ~�낵�������̒�����d�Ƃ���B�܂��A�}3-6�Ɏ����悤�ɁA�_O���璼��AF�ɍ~�낵�������̒�����h�Ƃ���Bh�����d���A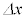 �Cn�Cα�̂����K�v�Ȃ��̂�p���ĕ\���B
�Cn�Cα�̂����K�v�Ȃ��̂�p���ĕ\���B
(2) �����ŗp����2�{�̌����́A���ꂼ��A�P�ʎ��Ԃ�����Q�̃G�l���M�[�������āA��������ˏo����Ă����B���ˊpθ����܊pϕ���������A�ݖ�T(5)�Ɠ����ߎ������藧�Ƃ��āA2�{�̌����������q�ɋy�ڂ����͂̑傫��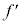 ���AQ�Cc�Cn�Cr�Cα�C
���AQ�Cc�Cn�Cr�Cα�C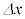 ��p���ĕ\���B�������Aθ��ϕ�͏\���ɏ��������߁A
��p���ĕ\���B�������Aθ��ϕ�͏\���ɏ��������߁A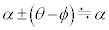 �Ƌߎ��ł��A���͂̌����͐��������Ƃ݂Ȃ����Ƃ��ł���B
�Ƌߎ��ł��A���͂̌����͐��������Ƃ݂Ȃ����Ƃ��ł���B
(3) 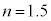 �C
�C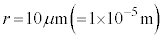 �C
�C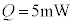 (
(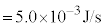 )�C
)�C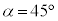 �Ƃ����Ƃ���A
�Ƃ����Ƃ���A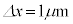 (
(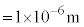 )�ł������B���̂Ƃ��A�O����������q�ɉ����Ă���͂̑傫��
)�ł������B���̂Ƃ��A�O����������q�ɉ����Ă���͂̑傫��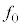 ���A�L������1���ŋ��߂�B�^�̌��̑�����
���A�L������1���ŋ��߂�B�^�̌��̑�����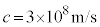 �ł���B�}3-5�C�}3-6�́Aα��
�ł���B�}3-5�C�}3-6�́Aα��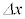 ���̑傫�������m�ł͂Ȃ��̂Œ��ӂ��邱�ƁB
���̑傫�������m�ł͂Ȃ��̂Œ��ӂ��邱�ƁB [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B