東大物理'21年前期[3]
2018年のノーベル物理学賞は、「レーザー物理学分野における画期的な発明」に対して授与され、そのうちの1つは光ピンセット技術に関するものであった。光ピンセットとは、レーザー光で微小な粒子等を捕捉する技術である。本問では、光が微粒子に及ぼす力を考察することで、光で微粒子が捕捉できることを確認してみよう。
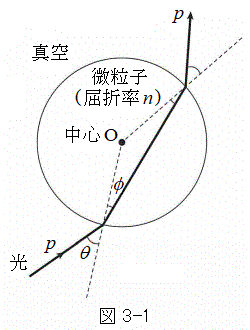 以下、図3-1に例を示すように、真空中に屈折率n (
以下、図3-1に例を示すように、真空中に屈折率n (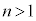 )の球形の微粒子があり、そこを光線が通過する状況を考える。光は光子という粒子の集まりの流れであり、光子は運動量をもつので、光の屈折に伴い光子の運動量が変化して、それが微粒子に力を及ぼすと考えられる。そこで以下では、光子の運動量の変化の大きさは、その光子が微粒子に及ぼす力積の大きさに等しいとする。また、光の吸収や反射の影響は無視する。さらに、微粒子に対して光線は十分に細く、光線の太さは考えない。
)の球形の微粒子があり、そこを光線が通過する状況を考える。光は光子という粒子の集まりの流れであり、光子は運動量をもつので、光の屈折に伴い光子の運動量が変化して、それが微粒子に力を及ぼすと考えられる。そこで以下では、光子の運動量の変化の大きさは、その光子が微粒子に及ぼす力積の大きさに等しいとする。また、光の吸収や反射の影響は無視する。さらに、微粒子に対して光線は十分に細く、光線の太さは考えない。
Ⅰ 図3-1に示すように、真空中の微粒子を光線が通過している。微粒子の中心Oは光線と同一平面内にある。微粒子は固定されており、動かない。図3-2に示すように、光線が微粒子に入射する点を点A,微粒子から射出する点を点Bとする。入射前の光線を延長した直線と、射出後の光線を延長した直線の交点を点Cとする。線分ABと線分OCの交点を点Dとする。以下の設問に答えよ。 (1) 光が微粒子に入射する際の入射角をθ,屈折角をϕとする。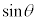 を、n,
を、n,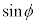 を用いて表せ。
を用いて表せ。
(2) 光線中を同じ方向に流れる光子の集まりがもつ、エネルギーの総量Eと運動量の大きさの総量pの間には、真空中では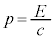 という関係が成り立つ。ここで、cは真空中の光の速さである。図3-1の光は、単位時間あたりQのエネルギーをもって、光源から射出されている。このとき、時間
という関係が成り立つ。ここで、cは真空中の光の速さである。図3-1の光は、単位時間あたりQのエネルギーをもって、光源から射出されている。このとき、時間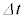 の間に射出された光子の集まりが真空中でもつ運動量の大きさの総量pを、Q,
の間に射出された光子の集まりが真空中でもつ運動量の大きさの総量pを、Q,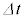 ,c,nのうち必要なものを用いて表せ。
,c,nのうち必要なものを用いて表せ。
(3) 図3-1に示すように、微粒子に入射する前の光子と、微粒子から射出した光子は、運動量の大きさは変わらないが、向きは変化している。時間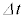 の間に射出された光子の集まりが、微粒子を通過することにより受ける運動量の変化の大きさの総量
の間に射出された光子の集まりが、微粒子を通過することにより受ける運動量の変化の大きさの総量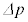 を、p,θ,ϕを用いて表せ。また、その向きを、点O,A,B,Cのうち必要なものを用いて表せ。
を、p,θ,ϕを用いて表せ。また、その向きを、点O,A,B,Cのうち必要なものを用いて表せ。
(4) この微粒子が光から受ける力の大きさf を、Q,c,θ,ϕのうち必要なものを用いて表せ。また、その向きを、点O,A,B,Cのうち必要なものを用いて表せ。
(5) 図3-2に示すように、OD間の距離をd,微粒子の半径をrとする。角度θ,ϕが小さいとき、設問Ⅰ(4)で求めた力の大きさf を、Q,c,n,r,dのうち必要なものを用いて表せ。小さな角度δに対して成り立つ近似式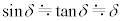 ,
,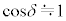 を使い、最終結果には三角関数を含めずに解答すること。
を使い、最終結果には三角関数を含めずに解答すること。
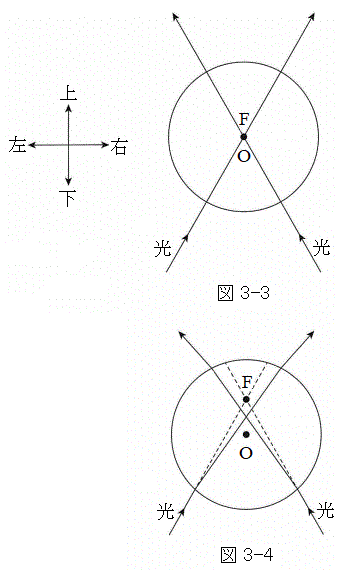 Ⅱ 図3-3,図3-4に示すように、強度(単位時間あたりのエネルギー)の等しい2本の光線が点Fで交わるよう光路を調整したうえで、設問Ⅰと同じ微粒子を、それぞれ異なる位置に置いた。いずれの図においても、入射光が鉛直線(上下方向)となす角度は2本の光線で等しく、2本の光線と微粒子の中心Oは同一平面内にある。微粒子は固定されており、動かない。以下の設問に答えよ。力の向きについては、設問の指示に従って、力が働く場合は図3-3の左側に図示した上下左右のいずれかを解答し、力が働かない場合は「力は働かない」と答えること。
Ⅱ 図3-3,図3-4に示すように、強度(単位時間あたりのエネルギー)の等しい2本の光線が点Fで交わるよう光路を調整したうえで、設問Ⅰと同じ微粒子を、それぞれ異なる位置に置いた。いずれの図においても、入射光が鉛直線(上下方向)となす角度は2本の光線で等しく、2本の光線と微粒子の中心Oは同一平面内にある。微粒子は固定されており、動かない。以下の設問に答えよ。力の向きについては、設問の指示に従って、力が働く場合は図3-3の左側に図示した上下左右のいずれかを解答し、力が働かない場合は「力は働かない」と答えること。
(1) 図3-3に示すように、微粒子の中心Oが点Fと一致しているとき、微粒子が2本の光から受ける合力の向きとして最も適切なものを「上」「下」「左」「右」「力は働かない」から選択せよ。
(2) 図3-4に示すように、微粒子の中心Oが点Fの下にあるとき、微粒子が2本の光から受ける合力の向きとして最も適切なものを「上」「下」「左」「右」「力は働かない」から選択せよ。点Fは微粒子の内部にあり、OF間の距離は十分小さいものとする。
(3) 設問Ⅱ(2)において、OF間の距離を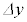 とするとき、微粒子が2本の光から受ける合力の大きさ
とするとき、微粒子が2本の光から受ける合力の大きさ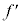 と
と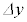 の間の関係について、最も適切なものを以下のア~エから選択せよ。なお、微粒子の半径rと比べて
の間の関係について、最も適切なものを以下のア~エから選択せよ。なお、微粒子の半径rと比べて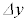 は小さく、設問Ⅰ(5)の近似が本設問でも有効である。図3-4は、
は小さく、設問Ⅰ(5)の近似が本設問でも有効である。図3-4は、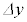 の大きさが誇張して描かれているので注意すること。
の大きさが誇張して描かれているので注意すること。 ア: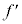 は
は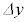 によらず一定である。
によらず一定である。 イ: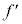 は
は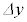 に比例する。
に比例する。 ウ: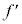 は
は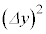 に比例する。
に比例する。 エ: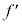 は
は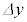 に反比例する。
に反比例する。
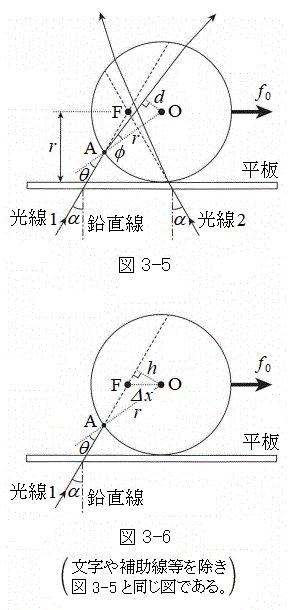 Ⅲ 図3-5に示すように、水平に置かれた薄い透明な平板の上方、高さrの位置にある点Fで、強度の等しい2本の光線(光線1,光線2)が交わるよう光路を調整したうえで、設問Ⅰ,設問Ⅱと同じ、半径rの微粒子を置いた。微粒子は常に平板と接触しており、微粒子と平板の間に摩擦はないものとする。微粒子には、外部から右向きに大きさ
Ⅲ 図3-5に示すように、水平に置かれた薄い透明な平板の上方、高さrの位置にある点Fで、強度の等しい2本の光線(光線1,光線2)が交わるよう光路を調整したうえで、設問Ⅰ,設問Ⅱと同じ、半径rの微粒子を置いた。微粒子は常に平板と接触しており、微粒子と平板の間に摩擦はないものとする。微粒子には、外部から右向きに大きさ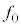 の力が働いており、この力と、2本の光線から受ける力が釣り合う位置で微粒子は静止している。すなわち、この微粒子は、光によって捕捉されている。OF間の距離は
の力が働いており、この力と、2本の光線から受ける力が釣り合う位置で微粒子は静止している。すなわち、この微粒子は、光によって捕捉されている。OF間の距離は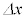 とし、点Fは、微粒子の内部、中心O付近にある。また、入射光が鉛直線となす角度αは2本の光線で等しく、2本の光線と点Oは同一平面内にある。平板は十分に薄く、平板による光の屈折や反射、吸収は考えない。光が微粒子に入射する際の入射角θは2本の光線で等しく、それに対する屈折角をϕとする。微粒子や平板の変形は考えない。
とし、点Fは、微粒子の内部、中心O付近にある。また、入射光が鉛直線となす角度αは2本の光線で等しく、2本の光線と点Oは同一平面内にある。平板は十分に薄く、平板による光の屈折や反射、吸収は考えない。光が微粒子に入射する際の入射角θは2本の光線で等しく、それに対する屈折角をϕとする。微粒子や平板の変形は考えない。
(1) 図3-5に示すように、光線1が微粒子に入射する点を点Aとし、微粒子の中心Oから微粒子内の光線1の上に降ろした垂線の長さをdとする。また、図3-6に示すように、点Oから直線AFに降ろした垂線の長さをhとする。hおよびdを、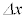 ,n,αのうち必要なものを用いて表せ。
,n,αのうち必要なものを用いて表せ。
(2) ここで用いた2本の光線は、それぞれ、単位時間あたりQのエネルギーをもって、光源から射出されていた。入射角θや屈折角ϕが小さく、設問Ⅰ(5)と同じ近似が成り立つとして、2本の光線が微粒子に及ぼす合力の大きさ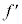 を、Q,c,n,r,α,
を、Q,c,n,r,α,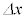 を用いて表せ。ただし、θとϕは十分に小さいため、
を用いて表せ。ただし、θとϕは十分に小さいため、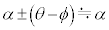 と近似でき、合力の向きは水平方向とみなすことができる。
と近似でき、合力の向きは水平方向とみなすことができる。
(3) 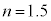 ,
,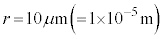 ,
,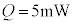 (
(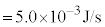 ),
),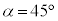 としたところ、
としたところ、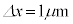 (
(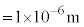 )であった。このとき、外部から微粒子に加えている力の大きさ
)であった。このとき、外部から微粒子に加えている力の大きさ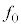 を、有効数字1桁で求めよ。真空中の光の速さは
を、有効数字1桁で求めよ。真空中の光の速さは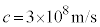 である。図3-5,図3-6は、αや
である。図3-5,図3-6は、αや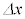 等の大きさが正確ではないので注意すること。
等の大きさが正確ではないので注意すること。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答医療機器などを中心に微細加工技術の開発が進んでいますが、さらに先を行く光ピンセット技術をテーマとした問題です。今までも、光子ヨットなど、光子がもつ運動量をネタとした問題が時々出題されています。Ⅱ(3)は正確に考察すると難しいので、試験会場では、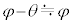 として直感的に解答する方がよいでしょう。
として直感的に解答する方がよいでしょう。
Ⅰ(1) 屈折の法則より、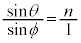 ∴
∴ 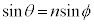 ......[答]
......[答]
(2) 時間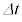 の間に射出された光子のエネルギーは、
の間に射出された光子のエネルギーは、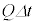 なので、このときの運動量の総量は、
なので、このときの運動量の総量は、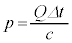 ......[答] (光電効果を参照)
......[答] (光電効果を参照) 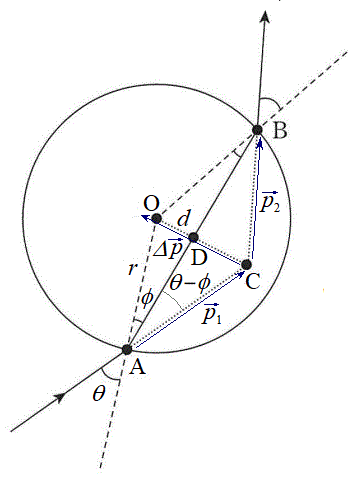
(3) Aから微粒子に入射する光子の集まりの運動量を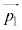 ,Bから射出される光子の集まりの運動量を
,Bから射出される光子の集まりの運動量を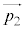 とすると、右図において、△ACBは二等辺三角形で、
とすると、右図において、△ACBは二等辺三角形で、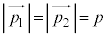 ,
,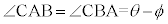 ,
,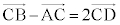 (//
(//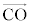 ),
),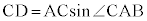 より、
より、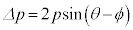 ......[答]
......[答] 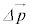 の向きは、
の向きは、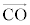 の向き ......[答]
の向き ......[答]
(4) 光子の集まりが受ける力積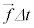 は、運動量の変化に等しく(運動量の原理を参照)、
は、運動量の変化に等しく(運動量の原理を参照)、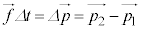
光子の集まりが受ける力は、微粒子が光から受ける力の反作用で、その大きさfは、 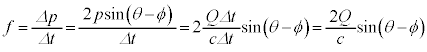 ......[答]
......[答]微粒子が受ける力の向きは、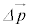 と逆向きで、
と逆向きで、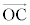 の向き ......[答]
の向き ......[答]
(5) 図3-2より、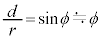 ・・・①,(1)の結果で問題文の近似を使うと、
・・・①,(1)の結果で問題文の近似を使うと、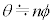 ・・・②,これより、
・・・②,これより、 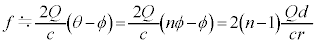 ......[答]
......[答]
Ⅱ(1) 2本の光線は屈折しないので運動量が変化しません。よって、微粒子は光線から力を受けず、「力は働かない」 ......[答]
(2) Ⅰ(4)の結果で、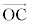 の向きは、微粒子の中心Oから微粒子内の屈折光に引く垂線の向きで、右図のように2光線について2つの向きは直線OFに関して対称で、合力は、「上」向き ......[答] です。
の向きは、微粒子の中心Oから微粒子内の屈折光に引く垂線の向きで、右図のように2光線について2つの向きは直線OFに関して対称で、合力は、「上」向き ......[答] です。
(3) ①,②より、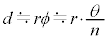 ・・・③
・・・③ 図3-4において、光線が微粒子に入射する点をAとし、直線FOと直線OAがなす角をφとする(点Aを定点とすればφは一定と考えられます)と、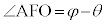 ,△AFOにおいて正弦定理より、
,△AFOにおいて正弦定理より、 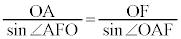 ,つまり、
,つまり、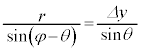
よって、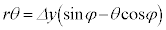
2次の微小量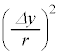 を無視すると、
を無視すると、 ③に代入して、
これより、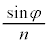 は一定なのでdは
は一定なのでdは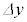 に比例します。Ⅰ(5)の結果より、微粒子が光線1の光子の集まりから受ける力の大きさfはdに比例するので、fは
に比例します。Ⅰ(5)の結果より、微粒子が光線1の光子の集まりから受ける力の大きさfはdに比例するので、fは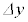 に比例します。光線2も同様で、2光線から受ける力の合力の大きさ
に比例します。光線2も同様で、2光線から受ける力の合力の大きさ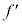 も
も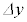 に比例します。よって、イ ......[答]
に比例します。よって、イ ......[答]
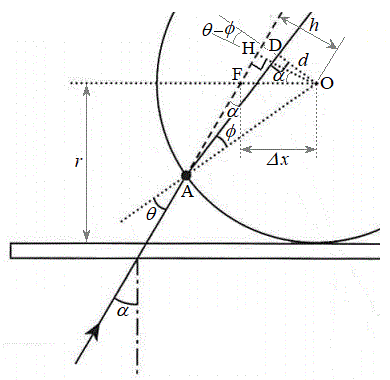 Ⅲ(1) Oから直線AF(光線1の入射方向を微粒子内まで伸ばした直線)に下ろした垂線の足をH,Oから光線1の微粒子内屈折光に下ろした垂線の足をDとすると、
Ⅲ(1) Oから直線AF(光線1の入射方向を微粒子内まで伸ばした直線)に下ろした垂線の足をH,Oから光線1の微粒子内屈折光に下ろした垂線の足をDとすると、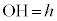 ,
,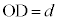 ,
,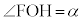 より、
より、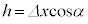 ......[答]
......[答]また、Ⅰ(1)の結果より、
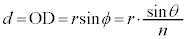 ・・・④
・・・④④に代入して、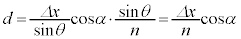 ......[答]
......[答] 別解.△OAHにおいて、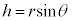 ,④とⅠ(1)より、
,④とⅠ(1)より、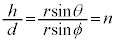
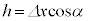 より、
より、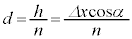
(2) Ⅰ(5)の結果より、微粒子が光線1から受ける力の大きさfは、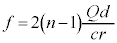 ,向きは、
,向きは、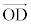 の向き。
の向き。 2本の光線から受ける力の合力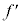 は、
は、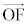 の方向で、
の方向で、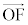 と
と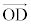 のなす角は、問題文より、
のなす角は、問題文より、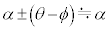 なので、合力の大きさは、
なので、合力の大きさは、 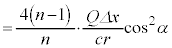 ......[答]
......[答](3) 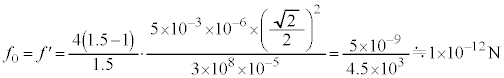 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 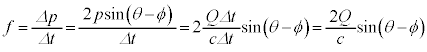 ......[答]
......[答]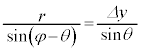
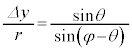 が微小で、問題文の指示より、
が微小で、問題文の指示より、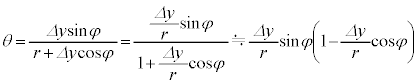 (
(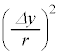 を無視すると、
を無視すると、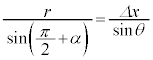 ∴
∴ 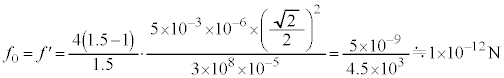 ......[答]
......[答]