運動量の原理 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物体の運動量の変化は、その間に物体が受けた力積に等しい。この原理を運動量の原理と言う。
運動方程式：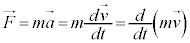
の両辺を、時間tについて、時刻tより時刻
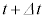までの範囲で積分(ベクトルの積分は、各成分ごとに積分すればよい)すると、
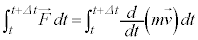
右辺の積分はtについての積分を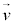
についての積分とみると(置換積分)、tが
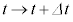と変わるとき、
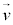は
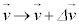と変わるとして、
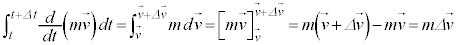
一方、積分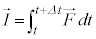
を力積と言います。
以上より、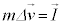
となり、運動量の変化が力積に等しいことがわかります。
なお、力積は、力が時間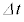
の間一定であれば、単に力と時間の積
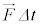(普通スカラーとベクトルの積はスカラーを左側に書くのですが、ここは便宜的にベクトルを左に書きます)になります。
力積の単位は、力×時間で、[Ns]となりますが、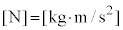
なので、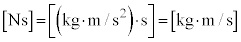
で運動量の単位と一致します。
大学入試の範囲では、一次元の運動において運動量の原理を理解しておけば充分です。
[例] 質量2kgの物体がx軸正方向に向かって速さ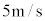
で運動している。この物体に3秒間にわたってx軸正方向に一定の力4Nを与えると速さはどうなるか。
物体の受ける力積は、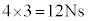
力を受けた後の物体の速さをvとして、運動量の原理より、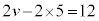
∴ 
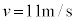
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。