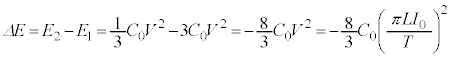東大物理'21年前期[2]
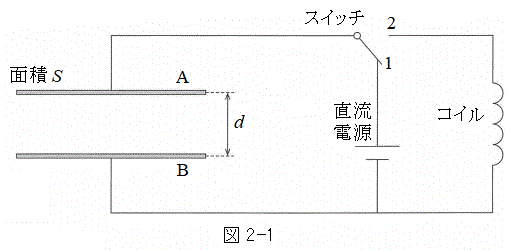 面積Sの厚みの無視できる金属の板Aと板Bを空気中で距離dだけ離して平行に配置した。dは十分に小さく、板の端の効果は無視する。図2-1のように、板、スイッチ、直流電源、コイルを導線でつないだ。直流電源の内部抵抗や導線の抵抗は無視できるほど小さい。空気の誘電率をεとする。
面積Sの厚みの無視できる金属の板Aと板Bを空気中で距離dだけ離して平行に配置した。dは十分に小さく、板の端の効果は無視する。図2-1のように、板、スイッチ、直流電源、コイルを導線でつないだ。直流電源の内部抵抗や導線の抵抗は無視できるほど小さい。空気の誘電率をεとする。
Ⅰ 図2-1のように、スイッチを1につなぎ、板Aと板Bの間に直流電圧V (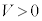 )を加えたところ、板A,Bにそれぞれ電荷Q,
)を加えたところ、板A,Bにそれぞれ電荷Q,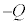 が蓄えられ、
が蓄えられ、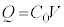 の関係があることが分かった。
の関係があることが分かった。
(1) 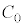 をS,d,εを用いて表せ。
をS,d,εを用いて表せ。 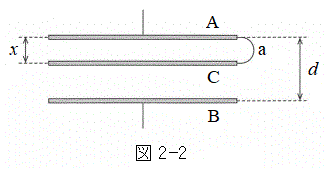 (2) 板A,Bと同じ形状をもつ面積Sの厚みの無視できる金属の板Cを図2-2のように板Aと板Bの間に互いに平行になるように差し入れた。板Aと板Cの距離はx (
(2) 板A,Bと同じ形状をもつ面積Sの厚みの無視できる金属の板Cを図2-2のように板Aと板Bの間に互いに平行になるように差し入れた。板Aと板Cの距離はx (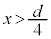 )である。さらに、板Aと板Cを太さの無視できる導線aで接続し、十分時間が経過したところ、板A,C,Bに蓄えられた電荷はそれぞれ一定となった。板A,C,Bからなるコンデンサーに蓄えられた静電エネルギーを求めよ。
)である。さらに、板Aと板Cを太さの無視できる導線aで接続し、十分時間が経過したところ、板A,C,Bに蓄えられた電荷はそれぞれ一定となった。板A,C,Bからなるコンデンサーに蓄えられた静電エネルギーを求めよ。
(3) 外力を加え、板Cをゆっくりと板Aに近づけて板Aと板Cの距離を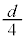 にした。導線aはやわらかく、板Cを動かすための力には影響がないとする。板Cに外力がした仕事Wを求めよ。また、Wは電源がした仕事
にした。導線aはやわらかく、板Cを動かすための力には影響がないとする。板Cに外力がした仕事Wを求めよ。また、Wは電源がした仕事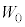 の何倍であるか正負の符号も含めて答えよ。
の何倍であるか正負の符号も含めて答えよ。
 Ⅱ 設問Ⅰ(3)の状態から、板A,B,Cと同じ形状をもつ面積Sの厚みの無視できる金属の板Dを、板Cと板Bの間に互いに平行になるように差し入れた。板Cと板Dの距離は
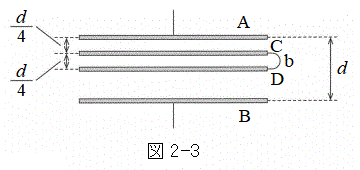
Ⅱ 設問Ⅰ(3)の状態から、板A,B,Cと同じ形状をもつ面積Sの厚みの無視できる金属の板Dを、板Cと板Bの間に互いに平行になるように差し入れた。板Cと板Dの距離は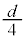 である。さらに、板Cと板Dを太さの無視できる導線bで接続した。十分時間が経過して各板に蓄えられた電荷がそれぞれ一定となった後に、図2-3のように導線aを外した。
である。さらに、板Cと板Dを太さの無視できる導線bで接続した。十分時間が経過して各板に蓄えられた電荷がそれぞれ一定となった後に、図2-3のように導線aを外した。
(1) 板Aに蓄えられた電荷は ,板Bに蓄えられた電荷は
,板Bに蓄えられた電荷は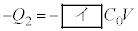 と表される。
と表される。 ,
, に入る数を答えよ。
に入る数を答えよ。
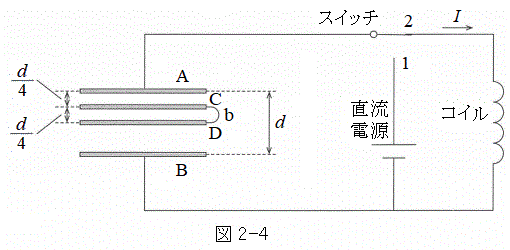
Ⅲ 設問Ⅱ(2)の状態から、時刻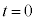 で図2-4のようにスイッチを1から2につなぎかえたところ、コイルには
で図2-4のようにスイッチを1から2につなぎかえたところ、コイルには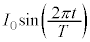 と表される電流Iが流れることが分かった。ただし、図中の矢印の向きを電流の正の向きにとる。コイルの抵抗は無視でき、自己インダクタンスはLである。他に説明がない場合は、直流電源の電圧は
と表される電流Iが流れることが分かった。ただし、図中の矢印の向きを電流の正の向きにとる。コイルの抵抗は無視でき、自己インダクタンスはLである。他に説明がない場合は、直流電源の電圧は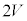 とする。
とする。
(1) TをLと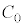 を用いて表せ。
を用いて表せ。
(2) 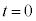 でコイルの両端にかかる電圧を答えよ。また、
でコイルの両端にかかる電圧を答えよ。また、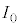 をT,V,Lを用いて表せ。ただし、微小時間
をT,V,Lを用いて表せ。ただし、微小時間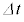 の間の電流変化は
の間の電流変化は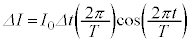 であることを用いてよい。
であることを用いてよい。
(3) 板A,Bの電荷をそれぞれ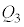 ,
,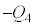 とすると、
とすると、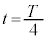 のとき
のとき の関係が成り立つ。
の関係が成り立つ。 に入る数を答えよ。また、
に入る数を答えよ。また、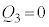 となる時刻
となる時刻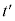 をTを用いて表せ。ただし
をTを用いて表せ。ただし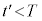 とする。
とする。
(4) 板A,C,D,Bからなるコンデンサーに蓄えられる静電エネルギーが、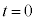 のときに
のときに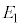 ,
,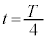 のときに
のときに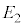 であった。
であった。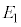 ,
,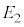 をそれぞれ
をそれぞれ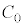 ,Vを用いて表せ。また、
,Vを用いて表せ。また、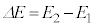 として、
として、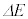 を
を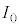 を含み、VおよびTを含まない形で表せ。
を含み、VおよびTを含まない形で表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 Ⅱでは、A-C間のコンデンサーとD-B間のコンデンサーは直列ではありません。コンデンサー回路は見かけでは直列か並列かを判断できないのです。Ⅲでは、直列と考えても同じ答えになります。
Ⅰ(1) 電荷Qから伸びる電気力線の本数は誘電率εの空気中で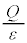 本です(ガウスの法則を参照)。面積Sの極板を覆う面積は
本です(ガウスの法則を参照)。面積Sの極板を覆う面積は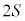 なので、単位面積あたりの電気力線の本数、つまり、板Aの周囲にできる電界は
なので、単位面積あたりの電気力線の本数、つまり、板Aの周囲にできる電界は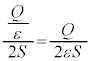 ,A-B間に板Aも板BもともにA→Bの方向に、電界
,A-B間に板Aも板BもともにA→Bの方向に、電界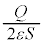 を作るので合成電界は
を作るので合成電界は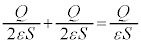 です。ところで、A-B間の電圧はV,極板間距離はdなので極板間の電界は
です。ところで、A-B間の電圧はV,極板間距離はdなので極板間の電界は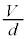 ,よって、
,よって、 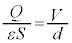 ∴
∴ 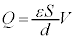
よって、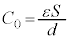 ......[答] (コンデンサーの公式より
......[答] (コンデンサーの公式より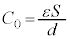 としてもOKでしょう)
としてもOKでしょう)
(2) C-B間の電気容量は、極板間距離が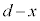 なので、
なので、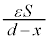 ,静電エネルギーは、
,静電エネルギーは、 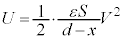 ......[答]
......[答]
(3) C-B間の距離が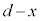 のとき、C-B間の電界は
のとき、C-B間の電界は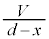 ,板Cに蓄えられる電荷は
,板Cに蓄えられる電荷は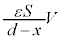 ,公式
,公式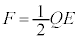 (コンデンサーを参照)より、極板間に働く静電気力は、
(コンデンサーを参照)より、極板間に働く静電気力は、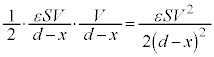 (引き合う向き),この力に逆らって
(引き合う向き),この力に逆らって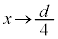 のときに外力がする仕事Wは、外力も移動方向もxが減る方向(外力の向きと板Cの移動方向が一致するので、外力は正の仕事をします)で、
のときに外力がする仕事Wは、外力も移動方向もxが減る方向(外力の向きと板Cの移動方向が一致するので、外力は正の仕事をします)で、 板Cに蓄えられる電荷は、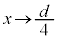 のときに、
のときに、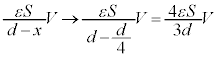 となるので、
となるので、 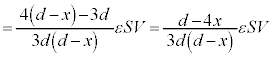 (
(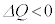 なので電荷は減少します)
なので電荷は減少します)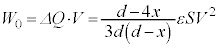 (
(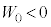 なので電池は負の仕事をしています)
なので電池は負の仕事をしています)①と比べて、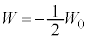 より
より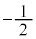 倍 ......[答]
倍 ......[答] 別解.(2)の結果で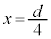 とすると、
とすると、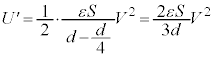 ,静電エネルギーは、
,静電エネルギーは、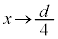 のときに、
のときに、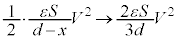 となるので、静電エネルギーの変化
となるので、静電エネルギーの変化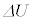 は、
は、 これより、エネルギー保存則(外力のした仕事Wと電池のした仕事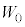 の和がコンデンサーの静電エネルギーの変化
の和がコンデンサーの静電エネルギーの変化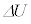 )から、
)から、
Ⅱ(1)(ア)(イ) 導線aを外す直前、A,C,Dは同電位です。B-D間にできるコンデンサーの電気容量は、極板距離が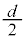 なのでⅠ(1)の結果より、
なのでⅠ(1)の結果より、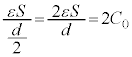 ,板Dには電荷
,板Dには電荷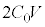 が蓄えられていて、導線aを外すと板Cと板Dに取り残されます。
が蓄えられていて、導線aを外すと板Cと板Dに取り残されます。 導線aを外すと、A-C間もコンデンサーとなり、静電容量は、極板間距離が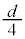 なので、
なので、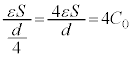
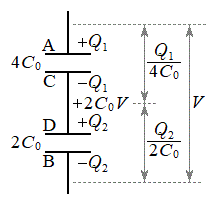 そこで、板Aに電荷
そこで、板Aに電荷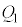 が蓄えられると、板Cには電荷
が蓄えられると、板Cには電荷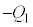 が蓄えられます。板Dに電荷
が蓄えられます。板Dに電荷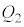 が蓄えられると、板Bには電荷
が蓄えられると、板Bには電荷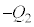 が蓄えられます。
が蓄えられます。
板Cと板Dの電荷の和は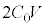 なので、
なので、 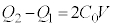 ・・・①
・・・①A-C間の電圧とD-B間の電圧の和はVなので、
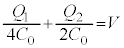 ,
,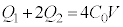 ・・・②
・・・②①+②より、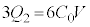 ∴
∴ 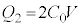 ,
,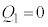 (ア) 0 (イ) 2 ......[答] (なお、合成容量を参照してください)
(ア) 0 (イ) 2 ......[答] (なお、合成容量を参照してください) 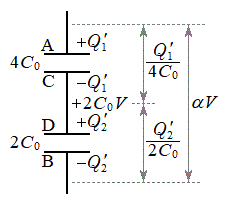 (2) 各板に蓄えられた電荷が一定になったときに、板Aに電荷
(2) 各板に蓄えられた電荷が一定になったときに、板Aに電荷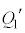 が蓄えられているとすると、板Cには
が蓄えられているとすると、板Cには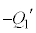 が蓄えられています。板Dに電荷
が蓄えられています。板Dに電荷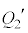 が蓄えられているとすると、板Bには電荷
が蓄えられているとすると、板Bには電荷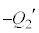 が蓄えられています。板Cと板Dには、元々合わせて
が蓄えられています。板Cと板Dには、元々合わせて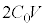 という電荷があったので、
という電荷があったので、
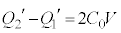 ・・・③
・・・③A-C間の電圧とD-B間の電圧の和は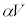 なので、
なので、 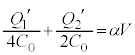 ,
,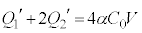 ・・・④
・・・④③+④より、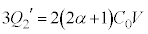
∴ 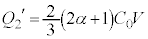 ,
,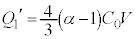 ・・・⑤
・・・⑤
板Aの板Cに対する電位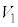 は、
は、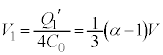 ......[答]板Dの板Bに対する電位
......[答]板Dの板Bに対する電位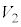 は、
は、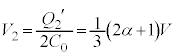 ......[答]
......[答]
Ⅲ(1) 時刻t におけるA-B間の電圧を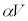 と考えると、Ⅱ(2)の結果が使えます。Ⅲでは、αは時刻tにより変化します。電流Iにより板Aの電荷が減少するので、⑤より、
と考えると、Ⅱ(2)の結果が使えます。Ⅲでは、αは時刻tにより変化します。電流Iにより板Aの電荷が減少するので、⑤より、 電流Iにより板Bの電荷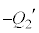 は増大するので、
は増大するので、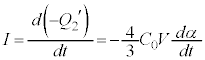 となりますが、⑥と一致します。キルヒホッフの第2法則より、コイルの逆起電力
となりますが、⑥と一致します。キルヒホッフの第2法則より、コイルの逆起電力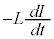 は、コンデンサーでの電圧降下
は、コンデンサーでの電圧降下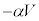 (電流Iの方向に回路を回ると、コンデンサーでは電圧降下は、板Aに対する板Bの電位になります)に一致するので、
(電流Iの方向に回路を回ると、コンデンサーでは電圧降下は、板Aに対する板Bの電位になります)に一致するので、 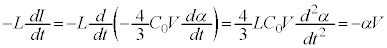 ・・・⑦
・・・⑦
∴ 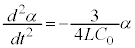
これより、αは、角振動数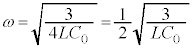 の単振動をします。問題文中のコイルの電流の式より単振動の周期はTで、周期Tは、
の単振動をします。問題文中のコイルの電流の式より単振動の周期はTで、周期Tは、 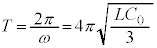 ......[答]
......[答]
(2) 問題文の式で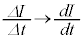 として、
として、 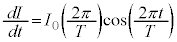 (電流Iの式を微分してもよいですが) ・・・⑧
(電流Iの式を微分してもよいですが) ・・・⑧ここで、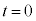 とすると、
とすると、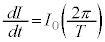 です。
です。
一方、直流電源の電圧は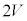 なので、スイッチの切り替え直後の
なので、スイッチの切り替え直後の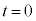 において
において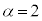 です。このとき、コイル両端の電圧降下
です。このとき、コイル両端の電圧降下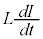 は、
は、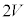 ......[答]よって、
......[答]よって、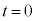 において、
において、 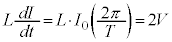 ∴
∴ 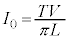 ......[答]
......[答]
(3) 問題文の板A,Bの電荷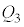 ,
,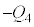 は、Ⅱ(2)またⅢ(1)の
は、Ⅱ(2)またⅢ(1)の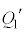 ,
,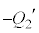 です。つまり、
です。つまり、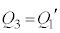 ,
,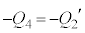
・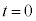 のとき、
のとき、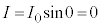 ,⑥より
,⑥より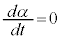 ,このときαは最大値2をとります。このとき、⑤で
,このときαは最大値2をとります。このとき、⑤で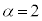 として、
として、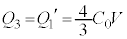 ,
,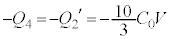 ,Ⅱ(2)の結果より、
,Ⅱ(2)の結果より、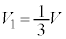 ,
,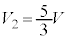
・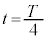 のとき、
のとき、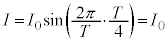 ,⑧より
,⑧より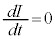 ,⑦より
,⑦より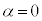 ,このとき⑤より、
,このとき⑤より、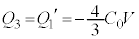 ,
,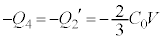 ,Ⅱ(2)の結果より、
,Ⅱ(2)の結果より、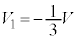 ,
,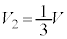
・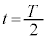 のとき、
のとき、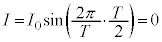 ,⑧より
,⑧より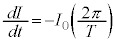 ,(2)の結果より、
,(2)の結果より、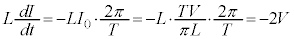 ,⑦より
,⑦より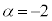 ,⑥より
,⑥より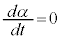 なので、このときαは最小値
なので、このときαは最小値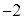 をとります。このとき、⑤で
をとります。このとき、⑤で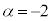 として、
として、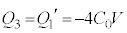 ,
,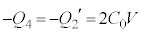 ,Ⅱ(2)の結果より、
,Ⅱ(2)の結果より、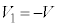 ,
,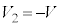
上記より、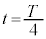 のとき、
のとき、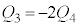 です。(ウ)
です。(ウ) 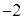 ......[答]⑤において、
......[答]⑤において、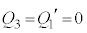 とすると、
とすると、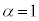 ,⑦より、
,⑦より、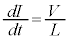
⑧と(2)の結果より、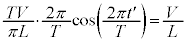 ∴
∴ 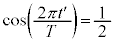
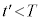 においては、
においては、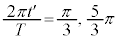 ∴
∴ 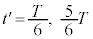 ......[答]
......[答]
(4) Ⅱ(1)より、A-C間の電気容量は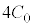 ,B-D間の電気容量は
,B-D間の電気容量は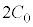 なので、(3)の
なので、(3)の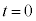 のときの
のときの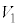 ,
,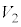 の値を用いて、
の値を用いて、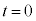 のときの静電エネルギー
のときの静電エネルギー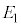 は、
は、 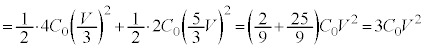 ......[答]
......[答](3)の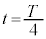 のときの
のときの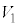 ,
,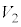 の値を用いて、
の値を用いて、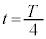 のときの静電エネルギー
のときの静電エネルギー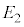 は、
は、 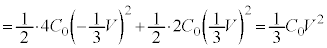 ......[答]
......[答]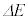 をV,Tを使わずに表すので、(1)の結果
をV,Tを使わずに表すので、(1)の結果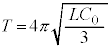 ,(2)の結果
,(2)の結果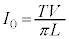 を使います。
を使います。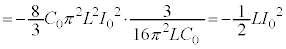 ......[答]
......[答]
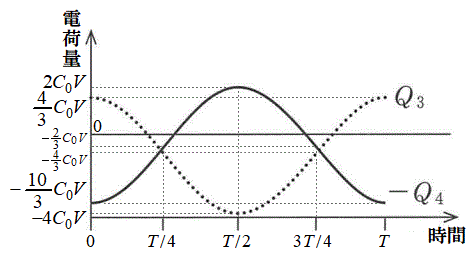 (5) 直流電源の電圧が
(5) 直流電源の電圧が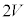 の場合から考えると、(3)の検討内容から考えて、④ ......[答] (
の場合から考えると、(3)の検討内容から考えて、④ ......[答] (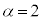 のときの各時刻の電気量の値は右図参照)
のときの各時刻の電気量の値は右図参照)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 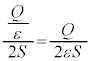 ,A-B間に板Aも板BもともにA→Bの方向に、電界
,A-B間に板Aも板BもともにA→Bの方向に、電界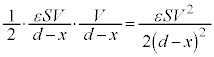 (引き合う向き),この力に逆らって
(引き合う向き),この力に逆らって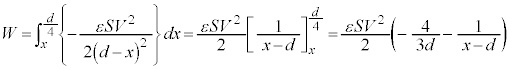
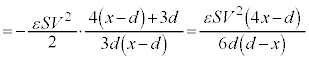 ......[答] ・・・① (
......[答] ・・・① (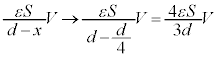 となるので、
となるので、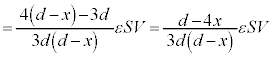 (
(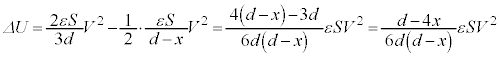
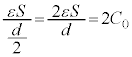 ,板Dには電荷
,板Dには電荷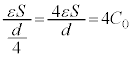
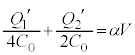 ,
,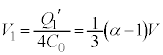 ......[答]
......[答]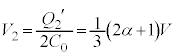 ......[答]
......[答]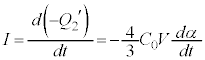 となりますが、⑥と一致します。キルヒホッフの第2法則より、コイルの逆起電力
となりますが、⑥と一致します。キルヒホッフの第2法則より、コイルの逆起電力