早大教育物理'08年[1]
銀河系には、原子時計並の高い精度の周期で電波のパルスを放射しているパルサーと呼ばれる天体が存在する。その信号を地球で観測すると、地球の公転周期のためにパルスの到達する時間がずれ、その変化から以下のように太陽の質量を求めることができる。
(A) ケプラーの第3法則と太陽の質量
問1 地球は太陽を中心に円運動しているとし、その半径を ,公転周期を
,公転周期を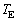 とする。太陽が地球に及ぼす重力は地球が受ける向心力に等しい。
とする。太陽が地球に及ぼす重力は地球が受ける向心力に等しい。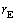 と
と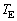 ,および重力定数(万有引力定数)Gを用いて太陽の質量を表せ。
,および重力定数(万有引力定数)Gを用いて太陽の質量を表せ。 この式を と
と の関係式とみなすと、ケプラーの第3法則になっている。以下に示すように、長期にわたってパルスを記録すると
の関係式とみなすと、ケプラーの第3法則になっている。以下に示すように、長期にわたってパルスを記録すると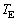 と
と が求まり、太陽の質量が決定される。
が求まり、太陽の質量が決定される。  (B) 到達時間の遅れ
(B) 到達時間の遅れ
簡単のためパルサーが地球の軌道面上にある場合を考える。パルサーの位置をA,太陽の位置をS,地球の位置はEとし、各天体間の距離を図1-1のように、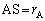 ,
, とする。パルサーと太陽を結ぶ直線を基準として太陽に対する地球の公転運動の回転角を、図1-1のようにθ [ラジアン]と定める。
とする。パルサーと太陽を結ぶ直線を基準として太陽に対する地球の公転運動の回転角を、図1-1のようにθ [ラジアン]と定める。
問2 天体の位置関係が図1-1のようなときに、地球とパルサーの距離EAを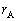 ,
,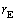 ,θ で表せ。
,θ で表せ。 ヒント:余弦定理 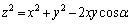
問3  に比べて
に比べて が十分に小さく、1と比べて
が十分に小さく、1と比べて は無視できないが
は無視できないが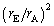 はゼロとみなせる近似のもとに考える。地球Eで観測される特定のパルスの到達時刻は、太陽Sで観測される同じパルスの到達時刻を基準にすると
はゼロとみなせる近似のもとに考える。地球Eで観測される特定のパルスの到達時刻は、太陽Sで観測される同じパルスの到達時刻を基準にすると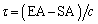 遅れる。ただし、cは光速である。τ は正負どちらの値もとり得る。τ を
遅れる。ただし、cは光速である。τ は正負どちらの値もとり得る。τ を ,c,θ で表せ。
,c,θ で表せ。 ヒント:pが1に比べ十分に小さいときqが実数であっても、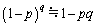 の近似が成立する。
の近似が成立する。 問4 τ を時間tの関数として表そう。まず、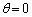 ラジアンとなる時刻を時間の原点
ラジアンとなる時刻を時間の原点 にとり、θ を
にとり、θ を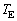 とtで表せ。この結果と問3をもとに、τ を
とtで表せ。この結果と問3をもとに、τ を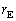 ,
,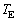 ,c,tで表せ。
,c,tで表せ。 問5 縦軸をτ にとり、横軸をtにとったグラフの概形を の範囲でかけ。縦軸には最大値と最小値を表す式を入れよ。
の範囲でかけ。縦軸には最大値と最小値を表す式を入れよ。 問6 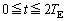 の間で、地球に到達するパルスの時刻が太陽に到達する時刻に比べて最も早くなる(τ が最小となる)のは、tがいくらといくらのときか。すべて書き出せ。
の間で、地球に到達するパルスの時刻が太陽に到達する時刻に比べて最も早くなる(τ が最小となる)のは、tがいくらといくらのときか。すべて書き出せ。 問7 τ の季節変動を測定できれば、問5の理論曲線との比較により、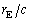 と
と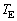 が精確に求まり、太陽の質量が問1より決まる。太陽の質量を1桁の精度で計算せよ。単位系はMKSでもcgsでもよいが、単位を書くこと。以下の数値を用いてよい。
が精確に求まり、太陽の質量が問1より決まる。太陽の質量を1桁の精度で計算せよ。単位系はMKSでもcgsでもよいが、単位を書くこと。以下の数値を用いてよい。 測定から得られる値の近似値:
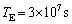
物理定数:重力定数(万有引力定数) 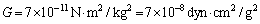
光速 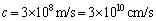
問8 地球で観測されるパルスとパルスの間隔は季節によって異なる。観測されるパルスの間隔が一番長くなるtを、 の範囲において求めよ。
の範囲において求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 恒星は、その寿命を全うする最後の時に急速に収縮して超新星爆発を起こします。恒星がその規模についてある条件をみたすと、超新星爆発を起こした後に、原子核がつぶれて陽子が電子を飲み込んで中性子となり、中性子ばかりとなった高密度な天体が残ります。この天体を中性子星と言いますが、高速で自転していると考えられていて、この高速な回転により、正確な周期の電波を放射します。これがパルサーです。
このパルサーからやってくる電波が到着する時刻の変化を測定することによって、太陽の質量を求めてみようという問題です。
実際には太陽表面に観測器を置くわけにはいかないので、惑星探査機と地球とで比べるのでしょうか?
問1 太陽の質量をM,地球の質量をmとします。地球の公転運動の角速度 は、
は、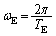 で与えられます。
で与えられます。 太陽が地球に及ぼす重力(万有引力)は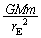 ,地球の円運動の向心力は
,地球の円運動の向心力は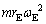 より、
より、 ∴ 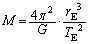 ......[答]この式は、地球の公転半径の3乗は公転周期の2乗に比例する、というケプラーの第3法則を意味しています。
......[答]この式は、地球の公転半径の3乗は公転周期の2乗に比例する、というケプラーの第3法則を意味しています。 ∴ 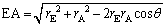 ......[答]
......[答] 問3  を微小量とするので、問2のEAの式の根号内を
を微小量とするので、問2のEAの式の根号内を でくくって
でくくって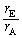 の形をひねり出します。
の形をひねり出します。 問題文中で指示されているように、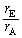 は無視せず、
は無視せず、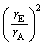 を無視し、
を無視し、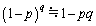 の近似を行うと、
の近似を行うと、 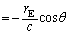 ......[答]
......[答]問4 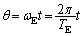 ......[答]
......[答] 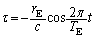 ......[答]
......[答]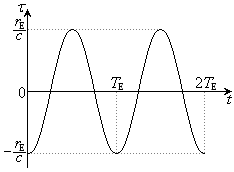 問5
問5 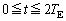 の範囲は2周期分です。最大値は
の範囲は2周期分です。最大値は ,最小値は
,最小値は です。右図に実線で示します。
です。右図に実線で示します。問6 最も早くなる、というのは、太陽よりも地球に早くパルス波がとどく、ということなので、問4のτ が最小の時刻として、 ......[答]
......[答] 問7 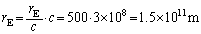
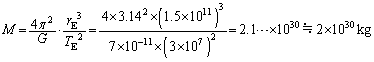 ......[答]
......[答]問8 ドップラー効果により、地球がパルサーに対して最も高速に遠ざかるときにパルス間隔が最も長くなります。パルサーは充分遠方にあって、パルサーから来る電波は太陽系にとどくときにはSAに平行にとどくと考えられます。従って、パルス間隔が最も長くなるのは、地球の速度が、SAに平行でパルサーから遠ざかる方向を向くときで、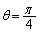 ,つまり、
,つまり、 ......[答] のときです。
......[答] のときです。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 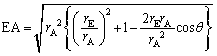


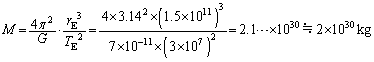 ......[答]
......[答]