�͊w(�͂̃��[�����g)���K���
��啨��'02�N[1]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 ����
����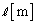 �̖_�̗��[�ɁA���ꂼ�ꎿ��
�̖_�̗��[�ɁA���ꂼ�ꎿ��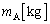 �C
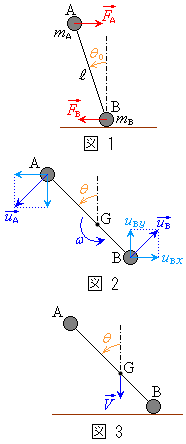
�C �̂�����A�CB�����t�������̂�����B������ŏ��A�}1�̂悤�ɁAB�𐅕��ȏ��ɂ����܂܁AA�ɂ͐��������E�����ɗ�
�̂�����A�CB�����t�������̂�����B������ŏ��A�}1�̂悤�ɁAB�𐅕��ȏ��ɂ����܂܁AA�ɂ͐��������E�����ɗ�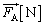 ���AB�ɂ͐��������������ɗ�
���AB�ɂ͐��������������ɗ�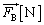 �������邱�Ƃɂ��A�����������甽���v����
�������邱�Ƃɂ��A�����������甽���v����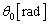 �����X������ԂŐÎ~�������B���̌�A��
�����X������ԂŐÎ~�������B���̌�A��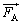 ��
��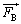 ���Ɏ�苎�����BB�͏����痣��邱�Ƃ͂Ȃ��AB�Ə��Ƃ̐ڐG�͊��炩�ł���Ƃ���B�^�����̕��̂̉�����������̌X����
���Ɏ�苎�����BB�͏����痣��邱�Ƃ͂Ȃ��AB�Ə��Ƃ̐ڐG�͊��炩�ł���Ƃ���B�^�����̕��̂̉�����������̌X���� �Ƃ��A�����v���𐳂Ƃ���B�d�͉����x�̑傫����
�Ƃ��A�����v���𐳂Ƃ���B�d�͉����x�̑傫����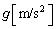 �Ƃ��A������̑傫���A�_�̎��ʂƑ����A��C�̒�R�͖����ł�����̂Ƃ��āA�ȉ��̖₢�ɓ�����B
�Ƃ��A������̑傫���A�_�̎��ʂƑ����A��C�̒�R�͖����ł�����̂Ƃ��āA�ȉ��̖₢�ɓ�����B
��1�@��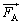 �Ɨ�
�Ɨ�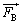 �ɂ�肱�̕��̂�
�ɂ�肱�̕��̂�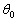 �����X������ԂŐÎ~�����Ă���Ƃ��A�_���炨����ɂ͂��炭�͖͂_�ɕ��s�ł���Ƃ��Ď��̏���ɓ�����B
�����X������ԂŐÎ~�����Ă���Ƃ��A�_���炨����ɂ͂��炭�͖͂_�ɕ��s�ł���Ƃ��Ď��̏���ɓ�����B (1) ��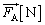 �̑傫����
�̑傫����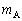 �C
�C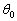 �Cg�ŕ\���B
�Cg�ŕ\���B (2) ������A�ɖ_����͂��炭�͂̑傫��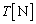 ��
��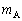 �C
�C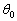 �Cg�ŕ\���B
�Cg�ŕ\���B (3) ������B�ɏ�����͂��炭�����R�͂̑傫��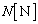 ��
��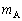 �C
�C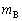 �Cg�ŕ\���B
�Cg�ŕ\���B ��2�@���̕��̂̏d�SG��A��B�����Ԑ���ɂ���B�d�SG����B�܂ł̋���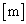 ��
��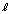 �C
�C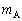 �C
�C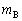 �ŕ\���B
�ŕ\���B ��3�@��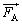 �Ɨ�
�Ɨ�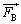 ���Ɏ�苎������A���̕��̂ɂ͐��������̗͂��͂��炩�Ȃ��̂ŁA�d�SG�̑��x
���Ɏ�苎������A���̕��̂ɂ͐��������̗͂��͂��炩�Ȃ��̂ŁA�d�SG�̑��x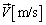 �͉��������̑��x�����݂̂����B����AA�CB�̑��x�́A�d�SG�̑��x�ƁA�d�SG�ɑ��邻�ꂼ��̑��Α��x�̍����ɂȂ�BA�CB�̏d�SG�ɑ��鑊�Ή^���́A�d�SG�𒆐S�Ƃ����]�^���ł���B���x�̐������������͉E�������A�������������͏���������ꂼ�ꐳ�Ƃ��A�܂��p���x�͔����v���𐳂Ƃ��Ď��̏���ɓ�����B
�͉��������̑��x�����݂̂����B����AA�CB�̑��x�́A�d�SG�̑��x�ƁA�d�SG�ɑ��邻�ꂼ��̑��Α��x�̍����ɂȂ�BA�CB�̏d�SG�ɑ��鑊�Ή^���́A�d�SG�𒆐S�Ƃ����]�^���ł���B���x�̐������������͉E�������A�������������͏���������ꂼ�ꐳ�Ƃ��A�܂��p���x�͔����v���𐳂Ƃ��Ď��̏���ɓ�����B (1) ����u�Ԃ̑��Ή^���̊p���x��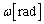 �C���̂Ƃ��̕��̂̉�����������̌X����θ �Ƃ���B�}2���Q�Ƃ���B�̏d�SG�ɑ��鑊�Α��x
�C���̂Ƃ��̕��̂̉�����������̌X����θ �Ƃ���B�}2���Q�Ƃ���B�̏d�SG�ɑ��鑊�Α��x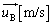 �̉�����������
�̉�����������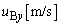 ��
�� �C
�C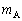 �C
�C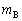 �Cθ�Cω �ŕ\���B
�Cθ�Cω �ŕ\���B (2) B�������痣��Ȃ��̂ŁAB�̑��x�̉������������͏��0�ƂȂ�B�}3�̂悤�ɉ�����������̌X����θ �̂Ƃ��A�d�SG�̑��x�͉����������ő傫����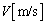 �ł������B���̂Ƃ��̑��Ή^���̊p���xω��
�ł������B���̂Ƃ��̑��Ή^���̊p���xω��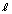 �C
�C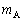 �C
�C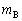 �Cθ�CV�ŕ\���B
�Cθ�CV�ŕ\���B (3) ���̂Ƃ���B�̑��x�̐�����������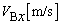 �CA�̑��x�̐�����������
�CA�̑��x�̐�����������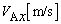 �Ɖ�����������
�Ɖ�����������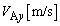 ���A
���A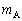 �C
�C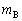 �Cθ�CV�̂�������K���Ȃ��̂�p���Ă��ꂼ��\���B
�Cθ�CV�̂�������K���Ȃ��̂�p���Ă��ꂼ��\���B [��]
��啨��'07�N�O��[1]
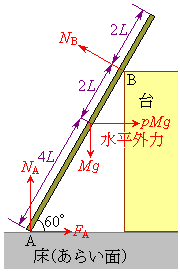 �}�̂悤�ɁA����
�}�̂悤�ɁA����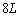 �C����M�ׂ̍���l�ȍ��̖_���A�����ȏ��̏�ɏ��Ɗp�x
�C����M�ׂ̍���l�ȍ��̖_���A�����ȏ��̏�ɏ��Ɗp�x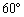 �ƂȂ�悤�ɒu����A��[����
�ƂȂ�悤�ɒu����A��[����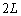 �̈ʒu�ő�̃J�h�Ɛڂ���悤�ɗ��Ă����Ă���B��̃J�h�͊��炩�ŁA�_�Ƃ̊Ԃɖ��C�͓͂����Ȃ��B���ʂ͂��炭�A�_�Ƃ̊Ԃɖ��C�͂������B�_�����ʂɐڂ���_��A�Ƃ��AA�ɂ����Ė_��������鐂���R�͂̑傫����
�̈ʒu�ő�̃J�h�Ɛڂ���悤�ɗ��Ă����Ă���B��̃J�h�͊��炩�ŁA�_�Ƃ̊Ԃɖ��C�͓͂����Ȃ��B���ʂ͂��炭�A�_�Ƃ̊Ԃɖ��C�͂������B�_�����ʂɐڂ���_��A�Ƃ��AA�ɂ����Ė_��������鐂���R�͂̑傫����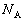 �C���C�͂�
�C���C�͂�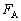 �Ƃ���B�܂��A�_����̃J�h�Ɛڂ���_��B�Ƃ��A�_�ɐ����ȕ����ɓ���B�ɂ�����R�͂̑傫����
�Ƃ���B�܂��A�_����̃J�h�Ɛڂ���_��B�Ƃ��A�_�ɐ����ȕ����ɓ���B�ɂ�����R�͂̑傫����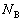 �Ƃ���B
�Ƃ���B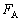 �̐��̕����͐}�Ɏ������̌����Ƃ���B�܂��A�_�Ə��ʂ̊Ԃ̐Î~���C�W����μ�C�d�͉����x��g�Ƃ���B�_�̒��S�ɂ͏d��
�̐��̕����͐}�Ɏ������̌����Ƃ���B�܂��A�_�Ə��ʂ̊Ԃ̐Î~���C�W����μ�C�d�͉����x��g�Ƃ���B�_�̒��S�ɂ͏d��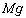 �������B
�������B
�T�D�����ȊO�͂�_�̒��S�ɉ������Ƃ���A�_�͐Î~�����܂܂ł������B�������A�����O�͂̑傫���͖_�̏d����p�{(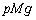 )�Ƃ��A�E�����ɓ����Ƃ���
)�Ƃ��A�E�����ɓ����Ƃ���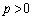 �Ƃ���B
�Ƃ���B ��1�@�_�ɓ����͂́A�_A�̂܂��̃��[�����g�̂肠�����A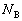 ���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B
���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B ��2�@�_�ɓ����͂̂肠�����A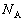 ���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B
���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B ��3�@�_�ɓ����͂̂肠�����A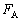 ���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B
���AM�CL�Cg�Cp�̂����̕K�v�Ȃ��̂�p���ĕ\���B ��4�@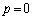 �̂Ƃ��ɖ_���Î~���Ă��邽�߂�μ�͈̔͂����߂�B
�̂Ƃ��ɖ_���Î~���Ă��邽�߂�μ�͈̔͂����߂�B �U�D���ɁA�_�������Ȃ��悤�Ɏ�Ŏx���Ă���A�_�̒��S�ɐ����O�͂��������B���_��������ƁA�����O��(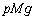 )�ƐÎ~���C�W��(μ)�̑傫���ɉ����āA�_�͐Î~�����܂܂��^�����n�߂邩�̂����ꂩ�ł���B�_���Î~�����܂܂ł��邽�߂ɂ́A����3�̏����������ɖ�������Ȃ���Ȃ�Ȃ��B
)�ƐÎ~���C�W��(μ)�̑傫���ɉ����āA�_�͐Î~�����܂܂��^�����n�߂邩�̂����ꂩ�ł���B�_���Î~�����܂܂ł��邽�߂ɂ́A����3�̏����������ɖ�������Ȃ���Ȃ�Ȃ��B (����a)�@��̃J�h(�_B)����_������Ȃ��B
(����b)�@������_������Ȃ��B
(����c)�@���ɐڂ���_�̒[�������ɂ��E�ɂ����ׂ�Ȃ��B
���̏ꍇ�A����b�́A����c����������Ă���Ƃ��ɂ́A�K����������Ă���B
��5�@�������̑傫�Ȑ����O��(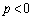 )���������Ƃ��ɁA����a���j��Ă��܂��B����a����������邽�߂́Ap�͈̔͂����߂�B
)���������Ƃ��ɁA����a���j��Ă��܂��B����a����������邽�߂́Ap�͈̔͂����߂�B ��6�@���̐Î~���C�W�����������Ƃ��ɏ���c���j��Ă��܂��B�_�̉��[�����ɂ��ׂ�Ȃ����߂�μ�C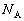 �C
�C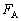 ���������ׂ���������K���Ɏ��ό`����ƁAp��μ�̊Ԃ̊W���Ƃ��Ď��̂悤�ɕ\����B(1)�C(2)�C(3)�ɓK���Ȑ�������B
���������ׂ���������K���Ɏ��ό`����ƁAp��μ�̊Ԃ̊W���Ƃ��Ď��̂悤�ɕ\����B(1)�C(2)�C(3)�ɓK���Ȑ�������B ��7�@���l�ɂ��āA�_�̉��[���E�ɂ��ׂ�Ȃ����߂�p��μ���������ׂ������͎����ŕ\����B(4)�C(5)�C(6)�ɓK���Ȑ�������B
[��]
��啨��'10�N���[1]
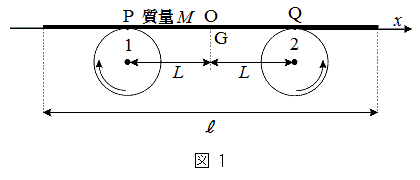 �}1�̂悤�ɁA���a�̓�������̉~��1��2���A�݂��ɋt�����ɓ����p���x�ʼn�]���Ă���B���̏�Ɏ���M�C�������Œ���
�}1�̂悤�ɁA���a�̓�������̉~��1��2���A�݂��ɋt�����ɓ����p���x�ʼn�]���Ă���B���̏�Ɏ���M�C�������Œ���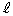 �̌������ł����l�Ȕ𐅕��ɏ悹���Ƃ��A���̔��ǂ̂悤�ȉ^�������邩�l�@���悤�B�~���̒����͔̕����傫���Ƃ���B�}1�͔̏d�SG���܂݁A�~���̉�]���ɐ����Ȓf�ʂ�\���Ă���B�~���͓��������ŁA��]���s�ɋ���
�̌������ł����l�Ȕ𐅕��ɏ悹���Ƃ��A���̔��ǂ̂悤�ȉ^�������邩�l�@���悤�B�~���̒����͔̕����傫���Ƃ���B�}1�͔̏d�SG���܂݁A�~���̉�]���ɐ����Ȓf�ʂ�\���Ă���B�~���͓��������ŁA��]���s�ɋ���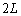 ��������Ēu����A�̒����������~���̉�]���ɐ����ɂȂ�悤�ɔ��悹���B�~���Ɣ̐ڐG�́A�~���̉�]���ɕ��s�ȕ����ɂ͈�l�ł���Ƃ���ƁA�̉^���͐}1�Ŏ������f�ʂōl���邱�Ƃ��ł���B�}�̂悤�ɔ̒��������ɉ����Đ���������x�����Ƃ�A�̉^����x����Ɍ��肳���Ƃ���B�Ɖ~��1�Ƃ̐ڐG�̒f�ʏ�̈ʒu��_P�Ƃ��A�~��2�Ƃ̐ڐG�̒f�ʏ�̈ʒu��_Q�Ƃ���B�_P�Ɠ_Q�̒��_�Ɍ��_O���Ƃ�A�}�̉E������x�̐��̌����Ƃ���B�Ɖ~���̊Ԃ̓����C�W���́A�ڐG�ʒu�̔Ɖ~���̑��Α��x�̑傫���ɂ�炸
��������Ēu����A�̒����������~���̉�]���ɐ����ɂȂ�悤�ɔ��悹���B�~���Ɣ̐ڐG�́A�~���̉�]���ɕ��s�ȕ����ɂ͈�l�ł���Ƃ���ƁA�̉^���͐}1�Ŏ������f�ʂōl���邱�Ƃ��ł���B�}�̂悤�ɔ̒��������ɉ����Đ���������x�����Ƃ�A�̉^����x����Ɍ��肳���Ƃ���B�Ɖ~��1�Ƃ̐ڐG�̒f�ʏ�̈ʒu��_P�Ƃ��A�~��2�Ƃ̐ڐG�̒f�ʏ�̈ʒu��_Q�Ƃ���B�_P�Ɠ_Q�̒��_�Ɍ��_O���Ƃ�A�}�̉E������x�̐��̌����Ƃ���B�Ɖ~���̊Ԃ̓����C�W���́A�ڐG�ʒu�̔Ɖ~���̑��Α��x�̑傫���ɂ�炸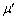 �ł���B�d�͉����x�̑傫����g�Ƃ���B
�ł���B�d�͉����x�̑傫����g�Ƃ���B
�T�D�ŏ��A�̏d�SG�����_O�ƈ�v����悤�ɔ��悹��ƁA�͐Î~�����܂܂ł������B
��1�@�~��1��2���ɋy�ڂ��Ă��鐂���R�͂����ꂼ��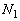 ��
��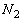 �Ƃ��A���������̗͂̂荇���A�d�SG�̂܂��̗͂̃��[�����g�̂荇�����l���A
�Ƃ��A���������̗͂̂荇���A�d�SG�̂܂��̗͂̃��[�����g�̂荇�����l���A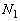 �����
�����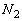 �����߂�B
�����߂�B 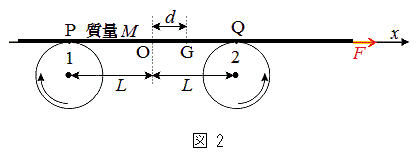 ���ɁA�}2�̂悤�ɔ̉E�[����ł������E����(x���̐��̌���)�Ɉ�������Ad (
���ɁA�}2�̂悤�ɔ̉E�[����ł������E����(x���̐��̌���)�Ɉ�������Ad (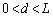 )�����ړ������Î~�������Ƃ���A�E�[�������͂�F�ƂȂ����B
)�����ړ������Î~�������Ƃ���A�E�[�������͂�F�ƂȂ����B
��2�@F�̑傫�������߂�B
��3�@��d�����ړ�������܂łɁA�肪�ɂ����d�������߂�B
���̌�A�Â��Ɏ�𗣂��Ɣ͍��E�ɉ����^�����n�߂��B�~���̊p���x�͏\���傫���A�����^���̑����́A�ڐG�̈ʒu�ɂ�����~���ƔƂ̑��Α��x�̑傫���ɔ�ׂāA�\���ɏ������Ƃ���B�������Ă���ꍇ�̗͂̃��[�����g�̂荇���̏����́A���~�܂��Ă���ꍇ�Ɠ����ƍl����B
��4�@���̉����^���̐U������ю��������߂�B
��5�@�̑������ő�ƂȂ�Ƃ��̏d�SG�̍��W�����߁A���̂Ƃ��̉^���G�l���M�[�����߂�B
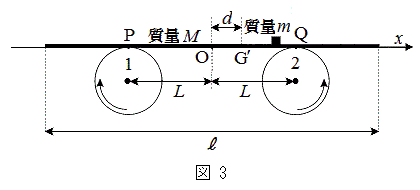 �U�D�}1�̏�Ԃ���A�}3�̂悤�ɑ傫���������ł��鎿��m�̂������̏�ɒu���ƁA������͔̏�����ׂ邱�ƂȂ��A�ƈꏏ�ɉ^�����n�߂��B�O�̉^���Ɠ������A�~���̊p���x�͏\���傫���A�^���̑����͐ڐG�̈ʒu�ɂ�����~���ƔƂ̑��Α��x�̑傫���ɔ�ׂď\���ɏ������Ƃ��A�������Ă���ꍇ�̗͂̃��[�����g�̂荇���̏����́A���~�܂��Ă���ꍇ�Ɠ����ƍl����B
�U�D�}1�̏�Ԃ���A�}3�̂悤�ɑ傫���������ł��鎿��m�̂������̏�ɒu���ƁA������͔̏�����ׂ邱�ƂȂ��A�ƈꏏ�ɉ^�����n�߂��B�O�̉^���Ɠ������A�~���̊p���x�͏\���傫���A�^���̑����͐ڐG�̈ʒu�ɂ�����~���ƔƂ̑��Α��x�̑傫���ɔ�ׂď\���ɏ������Ƃ��A�������Ă���ꍇ�̗͂̃��[�����g�̂荇���̏����́A���~�܂��Ă���ꍇ�Ɠ����ƍl����B
��6�@��������悹������ɁA�Ƃ�����Ƃ̑S�̂̏d�S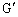 �̈ʒu���A
�̈ʒu���A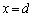 �ƂȂ邨����̍��W�����߂�B�������Ad�͇T�D�ōl�����}2��d�Ɠ����Ƃ���B
�ƂȂ邨����̍��W�����߂�B�������Ad�͇T�D�ōl�����}2��d�Ɠ����Ƃ���B ��7�@�Ƃ�����Ƃ̊Ԃ̐Î~���C�W����μ�Ƃ���ƁA�����肪�̏�����ׂ炸�ɁA���~�����痎�����邱�ƂȂ��A�����^���𑱂��邽�߂�μ�����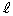 ���������ׂ����������߂�B
���������ׂ����������߂�B ��8�@���̉����^���̐U������ю����́A��4�̏ꍇ�̐U������ю����̂��ꂼ�ꉽ�{�ɂȂ邩���߂�B
��9�@�d�S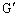 �̑������ő�ƂȂ����u�ԂɁA��������͂������B���̌�A�͉����^���𑱂����B���̉����^���̐U���́A�����肪����Ă���ꍇ�̉��{�ɂȂ邩���߂�B
�̑������ő�ƂȂ����u�ԂɁA��������͂������B���̌�A�͉����^���𑱂����B���̉����^���̐U���́A�����肪����Ă���ꍇ�̉��{�ɂȂ邩���߂�B [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B