コーシー・シュワルツの不等式
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
，
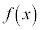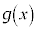が
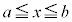において積分できるような関数であるとき、
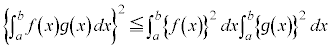
この不等式を、コーシー・シュワルツの不等式と言う。
[証明]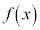 
，
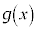が
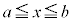において積分できるような関数であって、この範囲で
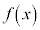が恒等的に0にはならないとします。
tを任意の実数として、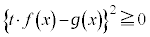
よっ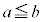て、
として、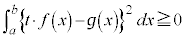
(定積分と不等式を参照)
不等号の等号は、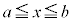
におけるすべてのxについて、
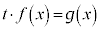であるときに成立します。
(∵ 
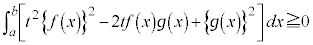
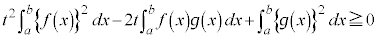
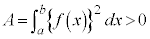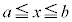におい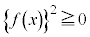て
であって、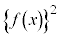
は恒等的に0ではない)，
，
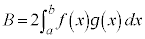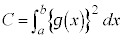とおくと、
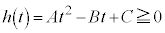
この不等式が成り立つ条件は、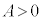
より、tに関する2次方程式：
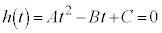が、相異なる2実数解をもたない(重解か2虚数解をもつ)こと(2次方程式の一般論を参照)で、2次方程式の判別式：
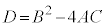について、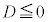
∴ 
∴ 
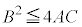
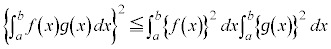
(証明終)
例．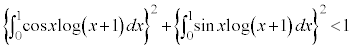 
を示す。
[解答] コーシー・シュワルツの不等式より、
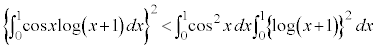
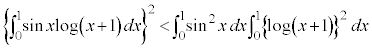
辺々加え合わせて、
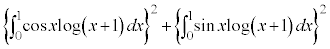
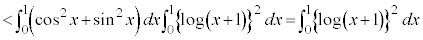
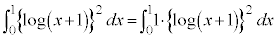
ここで、部分積分をするのですが、
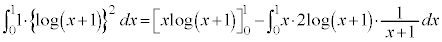
としてしまうと面倒なので、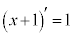
と見て以下のようにします。
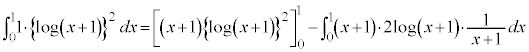
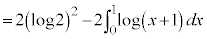
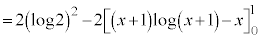
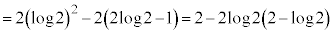
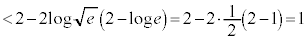
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
において、
より、