センター数学IA '06年第4問
袋A,B,C,Dがあり、それぞれに4枚のカードが入っている。各袋のカードには、1から4までの番号がつけられている。袋A,B,C,Dからカードを1枚ずつ取り出し、出た数をそれぞれa,b,c,dとする。
(1) a,b,c,dの最大の数が3以下である場合は 通りあり、最大の数が4である場合は
通りあり、最大の数が4である場合は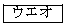 通りある。
通りある。
(2) a,b,c,dについて、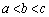 となる場合は
となる場合は 通りある。
通りある。
(3) 出た数a,b,c,dによって、次のように得点を定める。
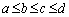 のときは、
のときは、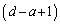 点
点
それ以外のときは、0点
(i) 得点が1点となる確率は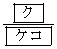 であり、得点が4点となる確率は
であり、得点が4点となる確率は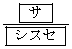 である。
である。
(ii) 得点の期待値は 点である。
点である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (1) 最大の数が3以下であるのは、各袋から取り出される数が、1か、2か、3の3通りのどれかに限られるときです。
各袋3通りずつで、各袋のどの1通りについても、他の袋は3通りのどの数もあり得ます。
a,b,c,dの最大の数が3以下となる場合は、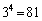 通り(場合の数を参照)。
通り(場合の数を参照)。
よって、[アイ]は81
4つの袋から出る数の出方は全部で、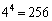 通り。このうち最大の数が4となるのは、最大の数が3以下の場合の81通りを除いた、
通り。このうち最大の数が4となるのは、最大の数が3以下の場合の81通りを除いた、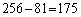 通り(場合の数の技巧を参照)。
通り(場合の数の技巧を参照)。
よって、[ウエオ]は175
(2) dが1から4のどの数であっても、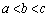 となるのは、a,b,cについて、
となるのは、a,b,cについて、
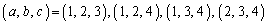
のいずれかの場合だから、a,b,c,dについて、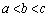 となる場合は、
となる場合は、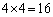 通り。
通り。
よって、[カキ]は16
(3)(i) 得点が1点となるのは、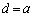 のときで、このとき
のときで、このとき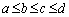 より、
より、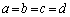
これが1から4まで、4通りあります。得点が1点となる確率は、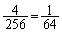
よって、[ク]は1,[ケコ]は64
得点が4点となるのは、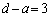 のときで、このとき、
のときで、このとき、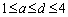 より、
より、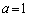 ,
,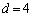 です。b,cについて、
です。b,cについて、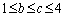 より、
より、
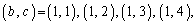
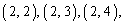
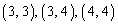
の10通り。得点が4点となる確率は、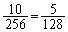
よって、[サ]は5,[シスセ]は128
(ii) 得点が2点となるのは、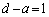 のときで、a,dについて、
のときで、a,dについて、
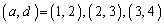
の3通りあります。
例えば、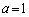 ,
,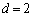 のとき、b,cについて、
のとき、b,cについて、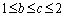 より、
より、
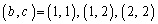
の3通りで、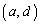 の3通りのどの1通りについても、
の3通りのどの1通りについても、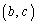 の3通りがあり得るので、a,b,c,dについて、
の3通りがあり得るので、a,b,c,dについて、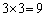 通り。
通り。
得点が2点となる確率は、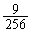
得点が3点となるのは、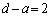 のときで、a,dについて、
のときで、a,dについて、
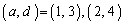
の2通りあります。
例えば、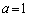 ,
,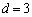 のとき、b,cについて、
のとき、b,cについて、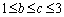 より、
より、
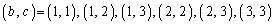
の6通りで、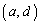 の2通りの各々についても、
の2通りの各々についても、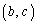 の6通りがあり得るので、a,b,c,dについて、
の6通りがあり得るので、a,b,c,dについて、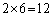 通り。
通り。
得点が3点となる確率は、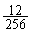
得点の期待値は、
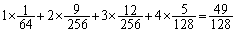
よって、[ソタ]は49,[チツテ]は128
センター試験の準備は、教科書の基礎事項をしっかりマスターし、ある程度、センター用の練習問題を解いたら、東京出版「センター試験必勝マニュアル 数学IA」(9月頃発売になります)を一通り読んでおきましょう。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。