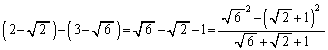センター数学IA '07年第2問
aを定数とし、xの2次関数
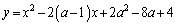･･･①
のグラフをGとする。
(1) グラフGが表す放物線の頂点の座標は
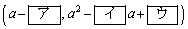
である。グラフGがx軸と異なる2点で交わるのは
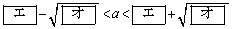
のときである。さらに、この二つの交点がともにx軸の負の部分にあるのは
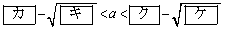
のときである。
(2) グラフGが表す放物線の頂点のx座標が3以上7以下の範囲にあるとする。
このとき、aの値の範囲は
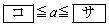
であり、2次関数①の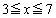
における最大値Mは
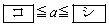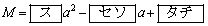
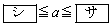のとき
のとき
である。
したがって、2次関数①の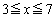
における最小値が6であるならば
であり、最大値Mは
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 私には、こういう問題の意義がわかりません。受験生泣かせの悪問ですが、難関大を狙う受験生の場合、これくらいの問題を軽く蹴散らしてくれるのでなければ修行不足と言うべきです。
放物線の頂点の座標は、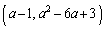
(ア) 1 (イ) 6 (ウ) 3 ......[答]グラフGがx軸と異なる2点で交わるのは、頂点のy座標が負のときで(2次方程式の一般論を参照)、
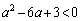
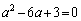を解くと、
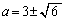より、
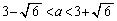･･･②(エ) 3 (オ) 6 ......[答]この二つの交点がともにx軸の負の部分にあるために、②に加えて、軸が
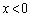の部分に存在し、Gとy軸との交点が
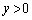の部分に来ることが必要十分です(2次方程式の解の配置を参照)。
軸が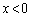
の部分にあるために、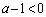
∴ 
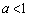･･･③Gとy軸との交点が
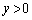の部分に来るために、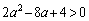
∴ 
，
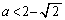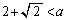･･･④
ここで、
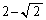と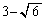
の大小関係が問題になります。
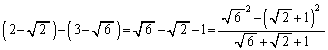
この分母は正で、分子は、
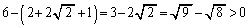
よって、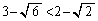
です。
従って、②かつ③かつ④より、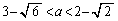
(カ) 3 (キ) 6 (ク) 2 (ケ) 2 ......[答]
(2) 放物線の頂点のx座標が3以上7以下なので、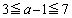
∴ 
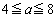･･･⑤(コ) 4 (サ) 8 ......[答]
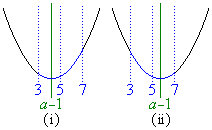軸が、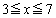
の範囲の左半分(
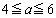)にあるか右半分にあるか(
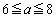)で場合分けします(右図、2次関数の最大・最小を参照)。(シ) 6 ......[答] (i)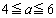 
のとき、軸が範囲の左半分の側にあるので、①は、範囲の右端
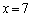において最大値Mをとり、 
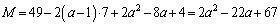(ス) 2 (セソ) 22 (タチ) 67 ......[答](ii)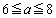 
のとき、軸が範囲の右半分の側にあるので、①は、範囲の左端
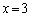において最大値Mをとり、 
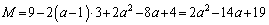･･･⑥(ツ) 2 (テト) 14 (ナニ) 19 ......[答]①は、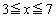
において、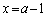
で最小値をとり、最小値が6なので、
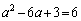
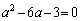･･･⑦
∴ 
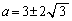⑤より、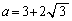
(ヌ) 3 (ネ) 2 (ノ) 3 ......[答]このとき、
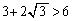より、上記(ii)の場合であって、⑥，⑦より、最大値Mは、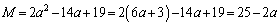
(ハヒ) 19 (フ) 4 (ヘ) 3 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
