�@�Z���^�[���wIA '07�N��3��@
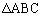 �ɂ����āA
�ɂ����āA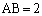 �C
�C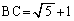 �C
�C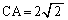 �Ƃ���B�܂��A
�Ƃ���B�܂��A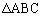 �̊O�ډ~�̒��S��O�Ƃ���B
�̊O�ډ~�̒��S��O�Ƃ���B
(1) ���̂Ƃ��A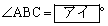 �ł���A�O�ډ~O�̔��a��
�ł���A�O�ډ~O�̔��a�� �@�@�@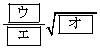
�ł���B (2) �~O�̉~����ɓ_D���A����AC�Ɋւ��ē_B�Ɣ��Α��̌ʂ̏�ɂƂ�B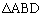 �̖ʐς�
�̖ʐς�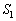 �C
�C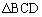 �̖ʐς�
�̖ʐς�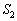 �Ƃ���Ƃ�
�Ƃ���Ƃ� �@�@�@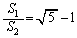 �@�@�@����@
�@�@�@����@
�ł���Ƃ���B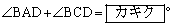 �ł��邩��
�ł��邩��
�@�@�@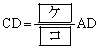
�ƂȂ�B���̂Ƃ�
�@�@�@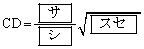
�ł���B
����ɁA2��AD�CBC�̉����̌�_��E�Ƃ��A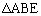 �̖ʐς�
�̖ʐς�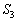 �C
�C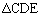 �̖ʐς�
�̖ʐς�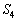 �Ƃ���B���̂Ƃ�
�Ƃ���B���̂Ƃ�
�@�@�@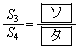 �@�@�@����A
�@�@�@����A
�ł���B�@�ƇA���
�@�@�@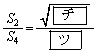
�ƂȂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Z���^�[�����Ƃ��ẮA������ނ̖��ł����A����Ƃē��ł͂Ȃ��̂ŁA�������蒚�J�Ɍ��Ă䂯�Ί����ł���͂��ł��B
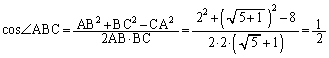 ��
�� 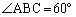
(�A�C) 60�@......[��]�����藝���A�O�ډ~�̔��a��R�Ƃ��āA
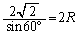
�� 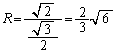
(�E) 2�@(�G) 3�@(�I) 6�@......[��]
(2) 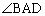 ��
��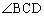 �́A�~�ɓ��ڂ���l�ӌ`�̑Ό�����p������A
�́A�~�ɓ��ڂ���l�ӌ`�̑Ό�����p������A 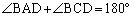 (�J�L�N) 180�@......[��]
(�J�L�N) 180�@......[��]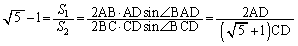 �@(�O�p�`�̖ʐ����Q��)��
�@(�O�p�`�̖ʐ����Q��)�� 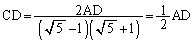
(�P) 1�@(�R) 2�@......[��]�O�p�`ACD�ɂ����āA�]���藝���A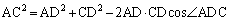
�����ŁA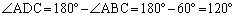 ���A
���A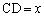 �Ƃ����ƁA
�Ƃ����ƁA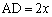 �ŁA
�ŁA
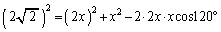
�� 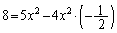 ��
�� 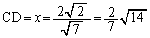
(�T) 2�@(�V) 7�@(�X�Z) 14�@......[��]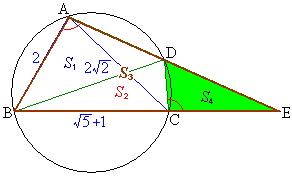
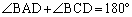 ���A
���A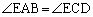
�܂��A�O�p�`ABE�ƎO�p�`CDE�Ƃɂ����āA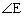 �͋��ʂȂ̂ŁA
�͋��ʂȂ̂ŁA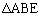 ��
��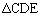
������́AAB�FCD = 2�F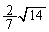 =
= 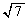 �F
�F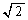
����āA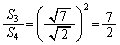 (�\) 7�@(�^) 2�@......[��]
(�\) 7�@(�^) 2�@......[��]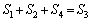 ���A
���A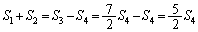
�@���A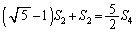
�� 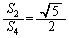
(�`) 5�@(�c) 2�@......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 