�@�Z���^�[���wIA '08�N��3��@
��ABC�ɂ����āA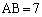 �C
�C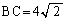 �C
�C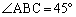 �Ƃ���B
�Ƃ���B
�܂��A��ABC�̊O�ډ~�̒��S��O�Ƃ���B
���̂Ƃ��A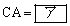 �ł���A�O�ډ~O�̔��a��
�ł���A�O�ډ~O�̔��a��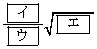 �ł���B
�ł���B
�O�ډ~O��̓_A���܂܂Ȃ���BC��ɓ_D��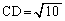 �ł���悤�ɂƂ�B
�ł���悤�ɂƂ�B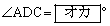 �ł��邩��A
�ł��邩��A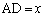 �Ƃ����x��2��������
�Ƃ����x��2��������
�@�@�@
�����B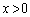 �ł��邩��
�ł��邩��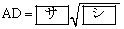 �ƂȂ�B
�ƂȂ�B
����
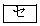
 �ɂ́A����
�ɂ́A���� �`
�` �̂������瓖�Ă͂܂���̂�����I�ׁB�������A�������̂��J��Ԃ��I��ł��悢�B
�̂������瓖�Ă͂܂���̂�����I�ׁB�������A�������̂��J��Ԃ��I��ł��悢�B
 AC�@
AC�@ AD�@
AD�@ AE�@
AE�@ BA�@
BA�@ CD�@
CD�@ ED
ED
�_A�ɂ�����O�ډ~O�̐ڐ��ƕ�DC�̉����Ƃ̌�_��E�Ƃ���B���̂Ƃ��A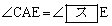 �ł��邩��A��ACE�Ɓ�
�ł��邩��A��ACE�Ɓ�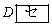 �͑����ł���B
�͑����ł���B
������A
�@�@�@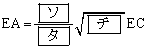
�ł���B�܂��A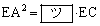 �ł���B����������
�ł���B����������
�@�@�@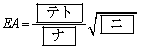
�ł���A��ACE�̖ʐς�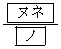 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ABC�ɂ����āA�]���藝���A
�� 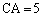
(�A) 5�@......[��]
�O�ډ~�̔��a��R�Ƃ��āA�����藝���A
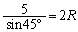 ��
�� 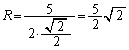
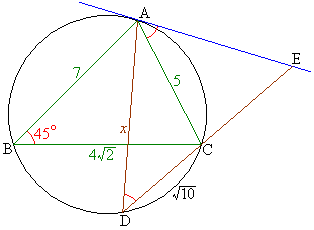 ����ʂ̏�ɗ��~���p�͓���������A
����ʂ̏�ɗ��~���p�͓���������A
(�I�J) 45�@......[��]
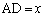 �Ƃ���ƁA��ADC�ɂ����āA�]���藝���A
�Ƃ���ƁA��ADC�ɂ����āA�]���藝���A
�������āA
(�L) 2�@(�N) 5�@(�P�R) 15�@......[��]
����������A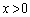 ���l�����āA
���l�����āA
(�T) 3�@(�V)5�@......[��]
�ڌ��p�̒藝���A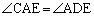 �@����@
�@����@
(�X)  �@......[��]
�@......[��]
��ACE�Ɓ�DAE�́A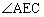 �����ʂŁA�@���A2�p���������Ȃ邩�瑊���ł��B
�����ʂŁA�@���A2�p���������Ȃ邩�瑊���ł��B
(�Z)  �@......[��]
�@......[��]
EC�FEA��CA�FAD��5�F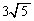
���A
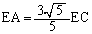 �@����A
�@����A
�܂��A���ׂ��̒藝���A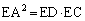 �@����B
�@����B
(�c)  �@......[��]
�@......[��]
�A���A
����ƁA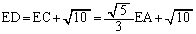 �Ƃ��B�ɑ�����āA
�Ƃ��B�ɑ�����āA
���ӂ�EA�Ŋ���A
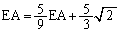 ��
�� 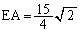
��ACE�̖ʐς́A
(�k�l) 75�@(�m) 8�@......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B