�@�Z���^�[���wIA '11�N��3��@
�_O�𒆐S�Ƃ���~O�̉~�����4�_A�CB�CC�CD�����̏��ɂ���B�l�p�`ABCD�̕ӂ̒����́A���ꂼ��
�ł���Ƃ���B
(1) 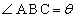 �C
�C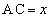 �Ƃ����ƁA��ABC�ɒ��ڂ���
�Ƃ����ƁA��ABC�ɒ��ڂ��� �ƂȂ�B�܂��A��ACD�ɒ��ڂ���
�ƂȂ�B����āA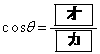 �C
�C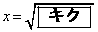 �ł���A�~O�̔��a��
�ł���A�~O�̔��a�� �ł���B
�ł���B
�܂��A�l�p�`ABCD�̖ʐς�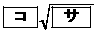 �ł���B
�ł���B
(2) �_A�ɂ�����~O�̐ڐ��Ɠ_D�ɂ�����~O�̐ڐ��̌�_��E�Ƃ���ƁA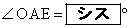 �ł���B�܂��A����OE�ƕ�AD�̌�_��F�Ƃ���ƁA
�ł���B�܂��A����OE�ƕ�AD�̌�_��F�Ƃ���ƁA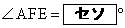 �ł���A
�ł���A �ł���B
����ɁA��AD�̉����Ɛ���OC�̉����̌�_��G�Ƃ���B�_E���璼��OG�ɐ��������낵�A����OG�Ƃ̌�_��H�Ƃ���B4�_E�CG�C �͓���~����ɂ���B
�͓���~����ɂ���B �ɓ��Ă͂܂���̂�����
�ɓ��Ă͂܂���̂����� �`
�` �����I�ׁB
�����I�ׁB C�CF�@
C�CF�@ H�CD�@
H�CD�@ H�CF�@
H�CF�@ H�CA�@
H�CA�@ O�CA����������
O�CA���������� �ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͖��W�Ȃǂł悭����������ł��B�ł����A�{�Ԃł́A(2)�œ�q�����������������̂ł͂Ȃ��ł��傤���H
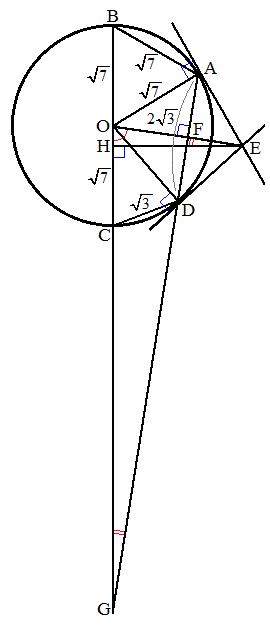 �r���ŁABC���~O�̒��a�ł��邱�Ƃ��킩���Ă��܂��̂ŁA�E�}�̂悤�Ȑ}��`���Ή��ł��Ȃ��̂ł����A��蕶�Ƃɂ�߂����ɂȂ��Ă��܂��ƍs���l�܂��Ă��܂����˂܂���B�}���`���ɂ����̂ł����A�}���`�������ǂ����ŏ����������ꂽ�Ǝv���܂��B
�r���ŁABC���~O�̒��a�ł��邱�Ƃ��킩���Ă��܂��̂ŁA�E�}�̂悤�Ȑ}��`���Ή��ł��Ȃ��̂ł����A��蕶�Ƃɂ�߂����ɂȂ��Ă��܂��ƍs���l�܂��Ă��܂����˂܂���B�}���`���ɂ����̂ł����A�}���`�������ǂ����ŏ����������ꂽ�Ǝv���܂��B
(1) �l�p�`ABCD�͉~�ɓ��ڂ���l�p�`�Ȃ̂ŁA�Ό�������p�݂͌��ɕ�p���Ȃ��A
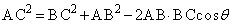
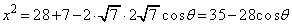 �@����@
�@����@(�A) 3�@(�C) 5 ......[��]
��ACD�ɂ����ė]���藝���A
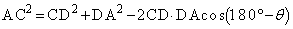
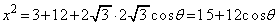 �@����A
�@����A(�E) 1�@(�G) 2 ......[��]
�@�C�A���A
�� 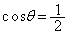
(�I) 1�@(�J) 2 ......[��]������A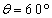 �ŁA�@���A
�ŁA�@���A 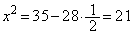 �C
�C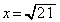
(�L) 2�@(�N) 1 ......[��]�~O�̔��a��R�Ƃ��āA�����藝���A �� 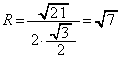
(�P) 7 ......[��]����ŁABC���~O�̒��a�ɂȂ��Ă��邱��(�_O��BC��̓_)���킩��̂ŁA�E�}��`�����Ƃ��ł��܂��B
��ABC���ʐ�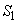 �́A
�́A ��ACD�̖ʐ�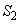 �́A
�́A �l�p�`ABCD�̖ʐς́A
(�R) 5�@(�T) 3 ......[��]
(2) 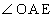 �́A���a�Ɛڐ��̂Ȃ��p��
�́A���a�Ɛڐ��̂Ȃ��p��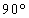 �ł��B
�ł��B (�V) 9�@(�X) 0 ......[��]���l��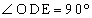 �C
�C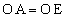 (���a)�COE���ʂɂ��A
(���a)�COE���ʂɂ��A ��OAE�߁�ODE
������AOE��AD�͒������A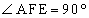 �ł��B(�Z) 9�@(�\) 0 ......[��]�܂��A��OAE�Ɓ�OFA�͑����Ȃ̂ŁAOA�FOE��OF�FOA��
�ł��B(�Z) 9�@(�\) 0 ......[��]�܂��A��OAE�Ɓ�OFA�͑����Ȃ̂ŁAOA�FOE��OF�FOA�� 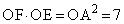 �@����B(�^) 7 ......[��]
�@����B(�^) 7 ......[��] �ʉ��D��AEF�̊O�ډ~���l����ƁAAE�͂��̉~�̒��a�A�܂��AOA�͂��̉~�̐ڐ��ł��B���ׂ��̒藝���A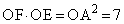
��EHO�Ɓ�GFO�͂ǂ����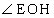 �����L���钼�p�O�p�`�ő����ł��B������A
�����L���钼�p�O�p�`�ő����ł��B������A ����2�p����HF�̏�ɗ��~���p�ƌ���AE�CG�CH�CF�͓���~����̓_�ł��B(�`)  ......[��]
......[��] �ʉ��D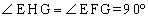 ���A����2�p�aEG�̏�ɗ��~���p�ƌ���AE�CG�CH�CF�͓���~����̓_�ł��B
���A����2�p�aEG�̏�ɗ��~���p�ƌ���AE�CG�CH�CF�͓���~����̓_�ł��B
��EHO�Ɓ�GFO�������ł��邱�Ƃ���A
OE�FOH��OG�FOF
�� 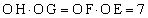 �@(�� �B)
�@(�� �B)
(�c) 7 ......[��] �ʉ��D�l�p�`EGHF�̊O�ډ~�ɕ��ׂ��̒藝��K�p���āA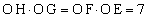
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �C
�C