センター数学IA '11年第4問
1個のさいころを投げるとき、4以下の目が出る確率pは
であり、5以上の目が出る確率qは
である。
以下では、1個のさいころを8回繰り返して投げる。
(1) 8回の中で4以下の目がちょうど3回出る確率は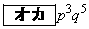
である。 第1回目に4以下の目が出て、さらに次の7回の中で4以下の目がちょうど2回出る確率は
である。
第1回目に5以上の目が出て、さらに次の7回の中で4以下の目がちょうど3回出る確率は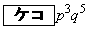
である。
(2) 次の
〜
のうち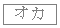
に等しいものは
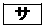と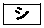
である。ただし、
と
は解答の順序を問わない。
(3) 得点を次のように定める。
8回の中で4以下の目がちょうど3回出た場合、
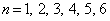について、第n回目に初めて4以下の目が出たとき、得点はn点とする。また、4以下の目が出た回数がちょうど3回とならないときは、得点を0点とする。
このとき、得点が6点となる確率は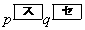
であり、得点が3点となる確率は
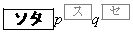である。また、得点の期待値は
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 序盤の凡ミスの連鎖反応で全滅、ということがないように工夫された出題になっています。(2)が意味不明ですが、(1)の結果から、パスカルの三角形を作るための公式：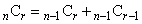
(組み合わせを参照)を意識させようというのでしょうか？
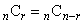を考えれば、2個はすぐ見つかります。
1個のさいころを投げるとき、4以下の目が出る確率pは、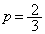
です。
(ア) 2 (イ) 3 ......[答]
5以上の目が出る確率qは、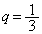
です。
(ウ) 1 (エ) 3 ......[答]
(1) 8回の中で4以下の目がちょうど3回出る確率は、反復試行の公式より、 (オ) 5 (カ) 6 ......[答]第1回目に4以下の目が出て(確率p)、さらに次の7回の中で4以下の目がちょうど2回出る(確率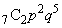
)確率は、 (キ) 2 (ク) 1 ......[答]第1回目に5以上の目が出て(確率q)、さらに次の7回の中で4以下の目がちょうど3回出る(確率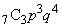
)確率は、 (ケ) 3 (コ) 5 ......[答]
注．(キク)と(ケコ)を合わせると(オカ)なので、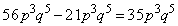
とすることもできます。
(2) 
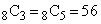，また、公式：
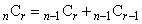より、 (サ) 
(シ) 
......[答] (サ，シは逆でもOK)
(3) 得点が6点になるのは、8回の中で4以下の目がちょうど3回出て、第6回目に初めて4以下の目が出る場合、つまり、1回目から5回目まで5以上の目が出て(確率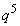
)、6回目、7回目、8回目には4以下の目が出る(確率
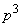)場合です。この確率は
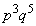です。 (ス) 3 (セ) 5 ......[答]得点が3点になるのは、1回目と2回目に5以上の目が出て(確率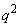
)、3回目に4以下の目が出て(確率p)、4回目から8回目までの5回のうち2回4以下の目が出る(
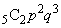)場合です。この確率は、
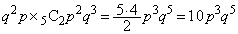(ソ) 1 (タ) 0 ......[答]得点が1点になるのは、1回目がpで、2回目から8回目までの7回のうち2回がpとなるときで、その確率は、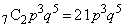
得点が2点になるのは、1回目がq，2回目がpで、3回目から8回目までの6回のうち2回がpとなるときで、その確率は、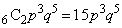
得点が4点になるのは、1回目から3回目がq，4回目がpで、5回目から8回目までの4回のうち2回がpとなるときで、その確率は、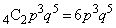
得点が5点になるのは、1回目から4回目がp，5回目がpで、6回目から8回目までの3回のうち2回がpとなるときで、その確率は、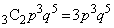
得点の期待値は、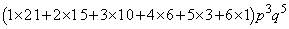
(チ) 1 (ツ) 1 (テ) 2 (ト) 7 (ナ) 2 (ヌ) 9 ......[答]
追記．この問題を解くのには関係ありませんが、(2)によると、
となり、(3)において、得点nが、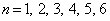
となる確率を加えると、8回の中で4以下の目がちょうど3回出る確率
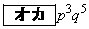になることがわかります。
一般的に言うと、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
(
(
，
(
)