共通テスト数学IA '22年第3問
複数人がそれぞれプレゼントを一つずつ持ち寄り、交換会を開く。ただし、プレゼントはすべて異なるとする。プレゼントの交換は次の手順で行う。
手順
外見が同じ袋を人数分用意し、各袋にプレゼントを一つずつ入れたうえで、各参加者に袋をでたらめに配る。各参加者は配られた袋の中のプレゼントを受け取る。
交換の結果、1人でも自分の持参したプレゼントを受け取った場合は、交換をやり直す。そして、全員が自分以外の人の持参したプレゼントを受け取ったところで交換会を終了する。
(1) 2人または3人で交換会を開く場合を考える。
(i) 2人で交換会を開く場合、1回目の交換で交換会が終了するプレゼントの受け取り方は
通りある。したがって、1回目の交換で交換会が終了する確率は
である。 (ii) 3人で交換会を開く場合、1回目の交換で交換会が終了するプレゼントの受け取り方は
通りある。したがって、1回目の交換で交換会が終了する確率は
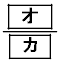である。 (iii) 3人で交換会を開く場合、4回以下の交換で交換会が終了する確率は
である。 (2) 4人で交換会を開く場合、1回目の交換で交換会が終了する確率を次の構想に基づいて求めてみよう。
構想
1回目の交換で交換会が終了しないプレゼントの受け取り方の総数を求める。そのために、自分の持参したプレゼントを受け取る人数によって場合分けする。
1回目の交換で、4人のうち、ちょうど1人が自分の持参したプレゼントを受け取る場合は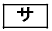
通りあり、ちょうど2人が自分のプレゼントを受け取る場合は
通りある。このように考えていくと、1回目のプレゼントの受け取り方のうち、1回目の交換で交換会が終了しない受け取り方の総数は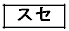
である。
したがって、1回目の交換で交換会が終了する確率は
である。 (3) 5人で交換会を開く場合、1回目の交換で交換会が終了する確率は
である。 (4) A，B，C，D，Eの5人が交換会を開く。1回目の交換でA，B，C，Dがそれぞれ自分以外の人の持参したプレゼントを受け取ったとき、その回で交換会が終了する条件付き確率は
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (4)は難問です。配点3点です。枠に合わなかったら、こだわらず次の問題に進むのが無難でしょう。
(1)(i) 2人をA，Bとし、プレゼントをa，bとすると、1回目の交換会で終了するのは、Aがbを受け取り、Bがaを受け取る(以後、A-b，B-aと表します)場合で1通りです。
ア 1 ......[答]プレゼントの受け取り方は、A-a，B-bとA-b，B-aの2通りあり、1回目の交換会で終了する確率は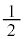
です。
イ 1 ウ 2 ......[答] (ii) 3人(A，B，Cとします)の交換会を開く場合、プレゼント(a，b，cとします)の受け取り方は、a，b，cの順列の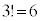
通りです。そのうち、1回目で終了するのは、A-b，B-c，C-aとA-c，B-a，C-bの2通りで、1回目で終了する確率は
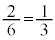です。 エ 2 オ 1 カ 3 ......[答]
(iii) 1回目で終了しない確率は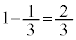
です。2回目で終了するのは、1回目に終了しなかったときで、その確率は
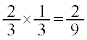，3回目で終了するのは、1回目と2回目で終了しなかったときで、その確率は
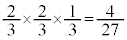，4回目で終了するのは、1回目、2回目、3回目で終了しなかったときで、その確率は
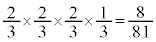です。4回以下で終了する確率は、 キク 65 ケコ 81 ......[答]
(2) 4人(A，B，C，Dとします)のうち、Aが自分の持参したプレゼントaを受け取るとき、B，C，Dが自分以外のプレゼント(b，c，dとします)を受け取るのは、(1)(ii)で考えたように2通りです。同様にB-bとなり、残る3人が自分以外のプレゼントを受け取るのも2通りです。C-c，D-dの場合もそれぞれ2通りで、ちょうど1人が自分の持参したプレゼントを受け取る場合は、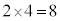
通りあります。 サ 8 ......[答]
A-a，B-bとなる場合に、CとDが自分以外の人が持参したプレゼントを受け取るのは、C-d，D-cの1通りで、4人から2人を選ぶ選び方が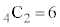
通りあり、ちょうど2人が自分のプレゼントを受け取る場合は、
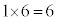通りあります。
シ 6 ......[答]
4人全員が自分のプレゼントを受け取るのが1通りあり、1回目の交換で交換会が終了しない受け取り方は、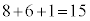
通り。
スセ 15 ......[答]プレゼントの受け取り方の総数は、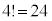
通りあります。4人とも自分以外の人のプレゼントを受け取り１回目で終了する受け取り方が
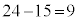通り。求める確率は、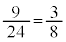
ソ 3 タ 8 ......[答] (3) 5人で交換会を開く場合プレゼントの受け取り方の総数は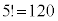
通りあります。A-aとなってB，C，D，Eの4人が自分以外の人が持参したプレゼントを受け取るのは、(2)で考えた通り9通りあり、5人の中から自分のプレゼントを受け取る1人の選び方が5通りで、
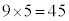通り。 A-a，B-bとなり、C，D，Eが自分以外の人が持参したプレゼントを受け取るのは2通りあり、5人から2人を選ぶ選び方が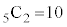
通りで、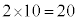
通り。A-a，B-b，C-cとなり、D-e，E-dとなるのは、1通りで、5人から3人を選ぶ選び方が
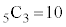通りで、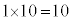
通り。5人全員が自分のプレゼントを受け取るのが1通り。1回目で終了する確率は、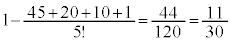
チツ 11 テト 30 ......[答] (4) 1回目の交換でA，B，C，Dがそれぞれ自分以外の人の持参したプレゼントを受け取ったとき、Eが自分のプレゼントを受け取る(E-e)場合と、自分以外の人のプレゼントを受け取る場合とがあります。
(i) E-eとなり、A，B，C，Dがそれぞれ自分以外の人のプレゼントを受け取るのは、(2)で調べたとおり、9通りあります。
(ii) E-aとなるとき、
・A-eとなるのは、B，C，Dの3人が自分以外の人のプレゼントを受け取るのが(1)(ii)で調べたように2通り。
・A-bとなる場合には、B，C，Dがe，c，dを受け取ることになりますが、B-e，C-d，D-cと、B-d，C-e，D-cと、B-c，C-d，D-eの3通りあり、A-cの場合も同様に3通り、A-dの場合も3通りあります。
このときは、合わせて、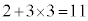
通りあります。E-bとなるとき、E-cとなるとき、E-dとなるときも同様に11通りずつあります。 よって、1回目の交換でA，B，C，Dがそれぞれ自分以外の人の持参したプレゼントを受け取る受け取り方は、(i)，(ii)合わせて、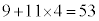
通りあります。
このうち、(i)は、Eが自分のプレゼントを受け取るので、交換会が終了しません。(ii)は、5人全員が自分以外の人のプレゼントを受け取るので、交換会が終了します。
よって、求める確率は、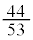
ナニ 44 ヌネ 53 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 