共通テスト数学IA '22年第4問
(1) 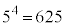 を
を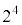 で割ったときの余りは1に等しい。このことを用いると、不定方程式
で割ったときの余りは1に等しい。このことを用いると、不定方程式 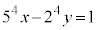 ・・・①
・・・①の整数解のうち、xが正の整数で最小になるのは
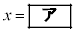 ,
,
であることがわかる。
また、①の整数解のうち、xが2桁の正の整数で最小になるのは
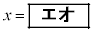 ,
,
である。
(2) 次に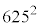 を
を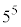 で割ったときの余りと、
で割ったときの余りと、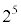 で割ったときの余りについて考えてみよう。
で割ったときの余りについて考えてみよう。 まず、
であり、また、 とすると
とすると である。これらより、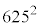 を
を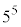 で割ったときの余りと、
で割ったときの余りと、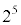 で割ったときの余りがわかる。
で割ったときの余りがわかる。 (3) (2)の考察は、不定方程式
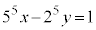 ・・・②
・・・②の整数解を調べるために利用できる。x,yを②の整数解とする。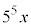 は
は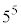 の倍数であり、
の倍数であり、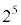 で割ったときの余りは1となる。よって、(2)により、
で割ったときの余りは1となる。よって、(2)により、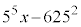 は
は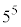 でも
でも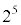 でも割り切れる。
でも割り切れる。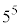 と
と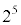 は互いに素なので、
は互いに素なので、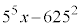 は
は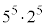 の倍数である。
の倍数である。
このことから、②の整数解のうち、xが3桁の正の整数で最小になるのは 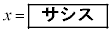 ,
,
であることがわかる。
(4) 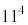 を
を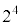 で割ったときの余りは1に等しい。不定方程式
で割ったときの余りは1に等しい。不定方程式 の整数解のうち、xが正の整数で最小になるのは
 ,
,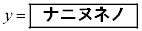
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 この問題も第3問と同様、最後の(4)は、時間があれば解答可能ですが、70分という制限時間では無理です。特に最後のナニヌネノの配点は2点です。イウから推量でテトをマークし、(4)は回避が得策です。
(1) 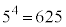 を
を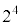 で割ると1余るので、mを整数として、
で割ると1余るので、mを整数として、
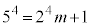 ,
,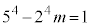 ・・・③
・・・③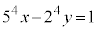 ・・・①
・・・①①-③より、
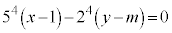 ・・・④
・・・④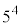 と
と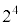 は互いに素なので、kを整数として、
は互いに素なので、kを整数として、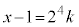 ,
,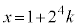
とおけます。xが正の整数で最小になるのは、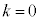 のときで、
のときで、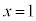
このとき、④,③より、 ア 1 イウ 39 ......[答]また、xが2桁の正の整数で最小になるのは、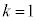 のときで、
のときで、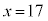
このとき、④より、 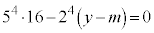 ∴
∴ 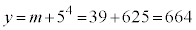
エオ 17 カキク 664 ......[答]
(2) 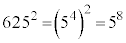 です。
です。 ケ 8 ......[答]
③を2乗すると、
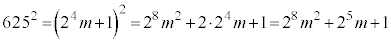 ・・・⑤
・・・⑤コ 5 ......[答]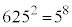 を5で割ったときの余りは0であり、
を5で割ったときの余りは0であり、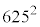 を
を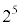 を割ったときの余りは1です。
を割ったときの余りは1です。 (3) 問題文の②式より、
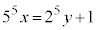 ・・・②
・・・②②-⑤より、
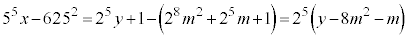 ・・・⑥
・・・⑥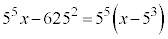 は、
は、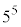 で割り切れますが、⑥より
で割り切れますが、⑥より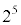 でも割り切れます。
でも割り切れます。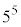 と
と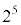 は互いに素なので、
は互いに素なので、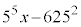 は
は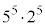 の倍数(整数を参照)で、lを整数として、
の倍数(整数を参照)で、lを整数として、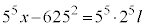 ・・・⑦
・・・⑦とおけます。つまり、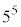 で割って、
で割って、 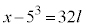 ∴
∴ 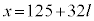
xが3桁の正の整数で最小になるのは、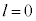 のときで、
のときで、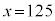
このとき、⑦は、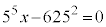 で、⑥と
で、⑥と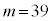 より、
より、 サシス 125 セソタチツ 12207 ......[答]
(4) 上記の過程をそのまま繰り返すのでは討ち死にします。⑦の5を11に置き換えると、
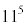 で割って、
で割って、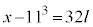 ∴
∴ 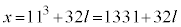
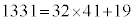 より、xが正の整数で最小になるのは、
より、xが正の整数で最小になるのは、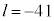 のときで、
のときで、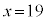 yは、
yは、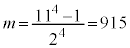 として⑥を使うのでは大変なので、パスカルの三角形風に簡易計算をして、
として⑥を使うのでは大変なので、パスカルの三角形風に簡易計算をして、与不定方程式より、
テト 19 ナニヌネノ 95624 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。