�@�Z���^�[���wIIB '06�N��2��@
a�𐳂̎����Ƃ��āA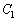 �C
�C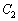 �����ꂼ�ꎟ��2�����̃O���t�Ƃ���B
�����ꂼ�ꎟ��2�����̃O���t�Ƃ���B
�@�@�@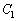 �F
�F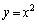
�@�@�@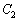 �F
�F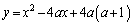
�܂��A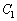 ��
��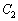 �̗����ɐڂ��钼����l�Ƃ���B
�̗����ɐڂ��钼����l�Ƃ���B
(1) �_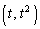 �ɂ�����
�ɂ�����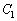 �̐ڐ��̕�������
�̐ڐ��̕�������
�@�@�@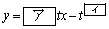
�ł���A���̒�����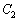 �ɐڂ���̂�
�ɐڂ���̂�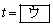 �̂Ƃ��ł���B
�̂Ƃ��ł���B
���������āA����l�̕�������
�@�@�@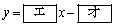
�ł���Al��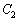 �̐ړ_�̍��W��
�̐ړ_�̍��W��
�@�@�@
�ł���B
(2) 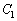 ��
��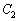 �̌�_��P�Ƃ���ƁAP�̍��W��
�̌�_��P�Ƃ���ƁAP�̍��W��
�@�@�@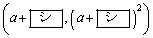
�ł���B�_P��ʂ��Ē���l�ɕ��s�Ȓ�����m�Ƃ���B����m�̕�������
�@�@�@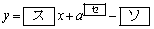
�ł���B����m��y���Ƃ̌�_��y���W�����ƂȂ�悤��a�̒l�͈̔͂�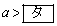 �ł���B
�ł���B
�@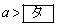 �̂Ƃ��A
�̂Ƃ��A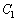 ��
��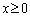 �̕����ƒ���m�����y���ň͂܂ꂽ�}�`�̖ʐ�S��a��p����
�̕����ƒ���m�����y���ň͂܂ꂽ�}�`�̖ʐ�S��a��p����
�@�@�@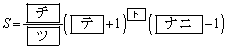
�ƕ\�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1) 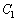 �̕���������������ƁA
�̕���������������ƁA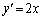
�_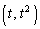 �ɂ�����
�ɂ�����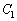 ���ڐ��̌X���́A
���ڐ��̌X���́A
�_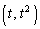 �ɂ�����
�ɂ�����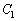 �̐ڐ��́A
�̐ڐ��́A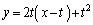
�������āA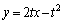 �@����@
�@����@
����āA[�A]��2�C[�C]��2
�@��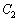 �̕�������A������ƁA
�̕�������A������ƁA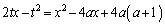
�������āA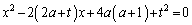 �@����A
�@����A
�@��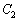 ���ڂ��邩��A�A�����ʎ�D��0
���ڂ��邩��A�A�����ʎ�D��0
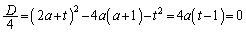
�� 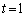
����āA[�E]��1
�]���āAl�̕������́A�@�ɂ����āA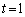 �Ƃ��āA
�Ƃ��āA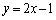 �@����B
�@����B
����āA[�G]��2�C[�I]��1
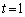 �̂Ƃ��A�A�́A
�̂Ƃ��A�A�́A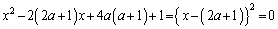
�� 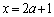
�B��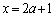 �Ƃ��āA
�Ƃ��āA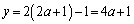
����āAl��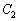 �̐ړ_�̍��W�́A
�̐ړ_�̍��W�́A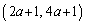
����āA[�J�L]��2a�C[�N]��1�C[�P�R]��4a�C[�T]��1
(2) 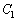 ��
��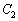 �̕�������A������ƁA
�̕�������A������ƁA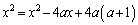
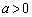 ���A
���A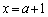
P�̍��W�́A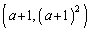
����āA[�V]��1
m�̌X���́A�B�̌X���Ɠ�����2 (2�����̕��s�E�������Q��)
�_P��ʂ�X��2�̒����Ƃ��āAm�F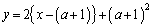
�������āAm�F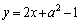
����āA[�X]��2�C[�Z]��2�C[�\]��1
����m��y���Ƃ̌�_��y���W����������A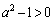
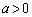 ���A
���A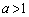
����āA[�^]��1
���߂��ʐ��́A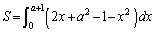
�@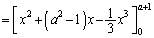
�@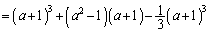
�@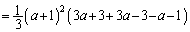
�@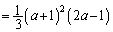
����āA[�`]��1�C[�c]��3�C[�e]��2�C[�i�j]��2a
�Z���^�[�����̏����́A���ȏ��̊�b��������������}�X�^�[���A������x�A�Z���^�[�p�̗��K������������A�����o�Łu�Z���^�[�����K���}�j���A���@���wIIB�v(9���������ɂȂ�܂�)����ʂ�ǂ�ł����܂��傤�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B