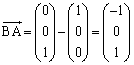�@�Z���^�[���wIIB '09�N��4��@
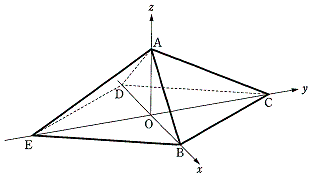 O�����_�Ƃ�����W��Ԃɂ�����5�_��A
O�����_�Ƃ�����W��Ԃɂ�����5�_��A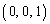 �CB
�CB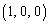 �CC
�CC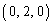 �CD
�CD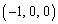 �CE
�CE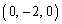 �Ƃ���B�Ђ��`BCDE���ʂƂ���l�p��A-BCDE�ƁA����ABC�ɕ��s�ȕ��ʂƂ̋��ʕ����ɂ��čl����B
�Ƃ���B�Ђ��`BCDE���ʂƂ���l�p��A-BCDE�ƁA����ABC�ɕ��s�ȕ��ʂƂ̋��ʕ����ɂ��čl����B
(1) 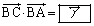 �ł���A�O�p�`ABC�̖ʐς�
�ł���A�O�p�`ABC�̖ʐς�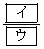 �ł���B
�ł���B (2) 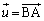 �C
�C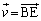 �Ƃ����B
�Ƃ����B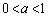 �Ƃ��A�_
�Ƃ��A�_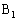 �����BE��a�F
�����BE��a�F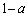 �ɓ�������_�Ƃ���ƁA
�ɓ�������_�Ƃ���ƁA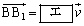 �ł���B�_
�ł���B�_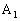 ��
�� �Œ�߁A����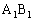 �Ɛ���AE������邱�Ƃ��������B
�Ɛ���AE������邱�Ƃ��������B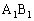 ��̓_P�́A
��̓_P�́A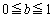 ����b��p����
����b��p���� �ƕ\�����B�܂��AAE��̓_Q�́A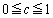 ����c��p����
����c��p���� �ƕ\�����BP��Q��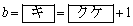 �̂Ƃ���v���邩��A����
�̂Ƃ���v���邩��A����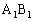 ��AE�́AAE��
��AE�́AAE��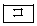 �F
�F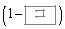 �ɓ�������_�Ō���邱�Ƃ��킩��B���̓_��
�ɓ�������_�Ō���邱�Ƃ��킩��B���̓_��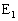 �Ƃ���B
�Ƃ���B
�_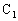 ��
�� �Œ�߂�ƁA���l�ɍl���邱�Ƃɂ��A����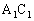 �Ɛ���AD���AAD��
�Ɛ���AD���AAD��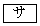 �F
�F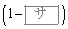 �ɓ�������_�Ō���邱�Ƃ��킩��B���̓_��
�ɓ�������_�Ō���邱�Ƃ��킩��B���̓_��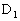 �Ƃ����
�Ƃ���� �ł���A�O�p�`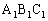 �͎O�p�`ABC�ƕ��s�ł��邩��A�l�p�`
�͎O�p�`ABC�ƕ��s�ł��邩��A�l�p�`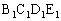 �̖ʐς�
�̖ʐς� �ł���B
�܂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��2��A��3��ɑ����ă{�����[�������Ղ����ԃx�N�g���̖��ł��B������Ƙ_���Ă����̂ł͂ƂĂ����Ԃ�����܂���B(�A)(�C)(�E)��(�c)(�e)(�g)�͏��X�v�Z���K�v�ł����A����ȊO�́A���͔h�̎��Ȃ�J���Ŗ��߂���A�Ƃ������A�J���ł���Ă����Ȃ��ƍ����_�͖]�߂܂���B
(1) 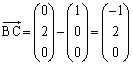 �C
�C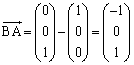
(�A) 1�@(�C) 3�@(�E) 2 ......[��]
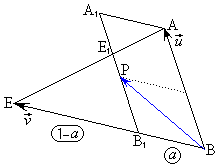 (2)
(2) 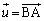 �C
�C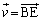 �Ƃ����̂ŁA�O�p�`ABE���܂ޕ��ʏ�̃x�N�g���́AB���n�_�Ƃ���悤�ɍl���邱�Ƃɂ��܂��BO���n�_�Ƃ���x�N�g���́A
�Ƃ����̂ŁA�O�p�`ABE���܂ޕ��ʏ�̃x�N�g���́AB���n�_�Ƃ���悤�ɍl���邱�Ƃɂ��܂��BO���n�_�Ƃ���x�N�g���́A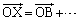 �̌`�ōl���܂��B
�̌`�ōl���܂��B�_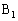 �͐���BE��a�F
�͐���BE��a�F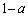 �ɓ�������̂ŁA
�ɓ�������̂ŁA (�G) a ......[��]
�����p����ƁA�_P��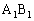 ��̓_�Ȃ̂ŁA
��̓_�Ȃ̂ŁA ��蕶��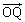 �̎��̌`����AAE��̓_Q�́AAE��
�̎��̌`����AAE��̓_Q�́AAE��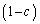 �Fc�ɓ�������_�Ƃ��āA
�Fc�ɓ�������_�Ƃ��āA �Ə�����̂ŁA
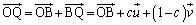 �@����A
�@����A(�I) c�@(�J) 1......[��]�@�C�A�́A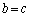 ����
����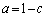 �C�܂�A
�C�܂�A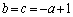 �̂Ƃ��Ɉ�v���܂��B(�L) c�@(�N) �|�@(�P) a ......[��]���̂Ƃ�Q�́AAE��a�F
�̂Ƃ��Ɉ�v���܂��B(�L) c�@(�N) �|�@(�P) a ......[��]���̂Ƃ�Q�́AAE��a�F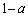 �ɓ�������_�ŁA����
�ɓ�������_�ŁA����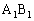 ��AE�́AAE��a�F
��AE�́AAE��a�F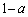 �ɓ�������_
�ɓ�������_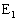 �Ō���邱�Ƃ��킩��܂��B(�R) a ......[��]
�Ō���邱�Ƃ��킩��܂��B(�R) a ......[��]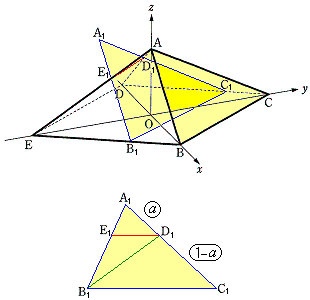 ��L�ŁAB��C�ɁA
��L�ŁAB��C�ɁA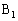 ��
��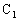 �ɁAE��D�ɓǂݑւ��邱�Ƃɂ��A����
�ɁAE��D�ɓǂݑւ��邱�Ƃɂ��A����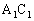 ��AD�́AAD��a�F
��AD�́AAD��a�F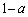 �ɓ�������_
�ɓ�������_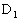 �Ō���邱�Ƃ��킩��܂��B(�T) a ......[��]
�Ō���邱�Ƃ��킩��܂��B(�T) a ......[��]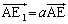 �C
�C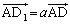 ���A
���A 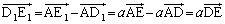 �@����B
�@����B(�V) a ......[��]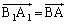 �Ɠ��l�ɁA
�Ɠ��l�ɁA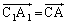 �C
�C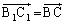
����āA�O�p�`ABC�ƎO�p�`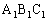 �͍����ł��B�܂��A
�͍����ł��B�܂��A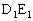 �FDE = a�F1�ŁA�O�p�`
�FDE = a�F1�ŁA�O�p�`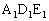 �ƎO�p�`
�ƎO�p�`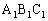 �͑����ȎO�p�`�ł����āA�������a�F1�Ŗʐς̔��
�͑����ȎO�p�`�ł����āA�������a�F1�Ŗʐς̔��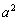 �F1�ł��B
�F1�ł��B
�O�p�`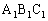 �̖ʐς͎O�p�`ABC�̖ʐςɓ�����
�̖ʐς͎O�p�`ABC�̖ʐςɓ�����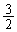 �ŁA�l�p�`
�ŁA�l�p�`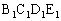 �̖ʐς́A�O�p�`
�̖ʐς́A�O�p�`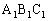 �̖ʐς���O�p�`
�̖ʐς���O�p�`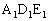 �̖ʐς������āA
�̖ʐς������āA (�X) 3�@(�Z) 2�@(�\) 1�@(�^) a�@(�`) 2 ......[��]�܂��A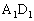 �F
�F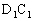 = a�F
= a�F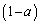 ���A
���A �� 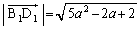
(�c) 5�@(�e) 2�@(�g) 2 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 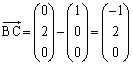 �C
�C