センター数学IIB '12年第1問
[1] 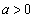 ,
,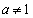 として、不等式
として、不等式 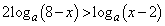 ・・・①
・・・①を満たすxの値の範囲を求めよう。
真数は正であるから、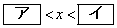 が成り立つ。ただし、対数
が成り立つ。ただし、対数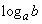 に対し、aを底といい、bを真数という。
に対し、aを底といい、bを真数という。
底aが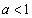 を満たすとき、不等式①
を満たすとき、不等式① 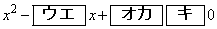 ・・・②
・・・②となる。ただし、 については、当てはまるものを、次の
については、当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
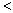

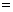

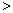 したがって、真数が正であることと②から、
したがって、真数が正であることと②から、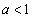 のとき、不等式①を満たすxのとり得る値の範囲は
のとき、不等式①を満たすxのとり得る値の範囲は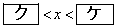 である。
である。
同様にして、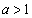 のときには、不等式①を満たすxのとり得る値の範囲は
のときには、不等式①を満たすxのとり得る値の範囲は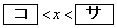 であることがわかる。
であることがわかる。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 対数の底が1より小さい場合も考えますが、この問題は落とせません。
真数は正であるから、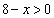 かつ
かつ 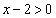
∴ 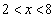 ・・・③
・・・③
(ア) 2 (イ) 8 ......[答]
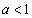 のとき、①より、
のとき、①より、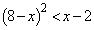
(ウ) 1 (エ) 7 (オ) 6 (カ) 6 (キ)  ......[答]
......[答]
∴ 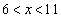
③と合わせて、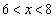
(ク) 6 (ケ) 8 ......[答]
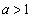 のとき、
のとき、
∴ 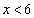 ,
,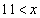
③と合わせて、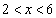
(コ) 2 (サ) 6 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[2] 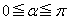 として
として を満たすβ について考えよう。ただし、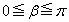 とする。
とする。
たとえば、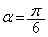 のとき、β のとり得る値は
のとき、β のとり得る値は と
と の二つである。
の二つである。
このように、αの各値に対して、β のとり得る値は二つある。そのうちの小さい方を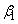 ,大きい方を
,大きい方を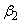 とし
とし が最大となるαの値とそのときのyの値を求めよう。
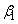 ,
,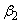 をαを用いて表すと、
をαを用いて表すと、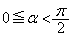 のときは
のときは 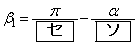 ,
,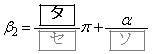
となり、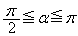 のときは
のときは 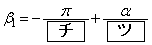 ,
,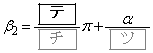
となる。
したがって、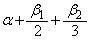 のとり得る値の範囲は
のとり得る値の範囲は である。よって、yが最大となるαの値は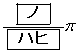 であり、そのときのyの値は
であり、そのときのyの値は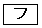 であることがわかる。
であることがわかる。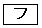 に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
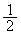
 1
1 
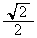

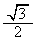
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 後半部分がややこしいですが、2つの場合に分けて、ていねいに解答しましょう。なお、三角関数を参照してください。
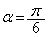 のとき
のとき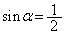 より、
より、
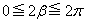 より、
より、
∴ 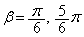
(シ) 6 (ス) 5 ......[答]
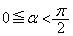 のとき、
のとき、
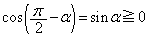 ,
,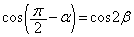
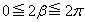 より、
より、
∴ 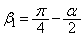 ,
,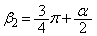
(セ) 4 (ソ) 2 (タ) 3 ......[答]
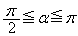 のとき、
のとき、
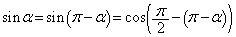 ,
,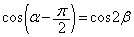
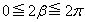 より、
より、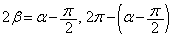
∴ 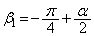 ,
,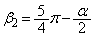
(チ) 4 (ツ) 2 (テ) 5 ......[答]
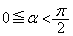 のとき、
のとき、
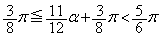 より、
より、
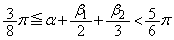 ・・・①
・・・①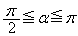 のとき、
のとき、
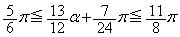 より、
より、
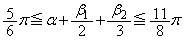 ・・・②
・・・②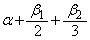 のとり得る値の範囲は、①,②より、
のとり得る値の範囲は、①,②より、
(ト) 3 (ナ) 8 (ニ) 1 (ヌ) 1 (ネ) 8 ......[答]
このとき、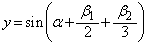 は、
は、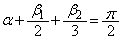 のとき、つまり、①の方なので、
のとき、つまり、①の方なので、
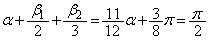 ,
,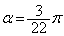
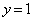 をとります。
をとります。
(ノ) 3 (ハ) 2 (ヒ) 2 (フ)  ......[答]
......[答]
数学TOP TOPページに戻る
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  の二つである。
の二つである。

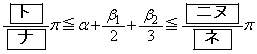
 であり、そのときのyの値は
であり、そのときのyの値は