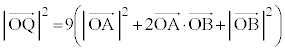�@���ʃe�X�g���wIIB '22�N��5��@
���ʏ�̓_O�𒆐S�Ƃ��锼�a1�̉~����ɁA3�_A�CB�CC������A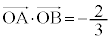 �����
�����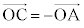 �����Ƃ���Bt ��
�����Ƃ���Bt ��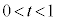 ���������Ƃ��A����AB��t �F
���������Ƃ��A����AB��t �F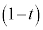 �ɓ�������_��P�Ƃ���B�܂��A����OP��ɓ_Q���Ƃ�B
�ɓ�������_��P�Ƃ���B�܂��A����OP��ɓ_Q���Ƃ�B
(1) 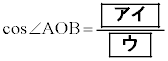 �ł���B
�ł���B �܂��A����k��p���āA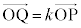 �ƕ\����B���������āA
�ƕ\����B���������āA 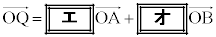 �@����@
�@����@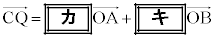
�ƂȂ�B
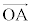 ��
��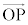 �������ƂȂ�̂́A
�������ƂȂ�̂́A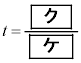 �̂Ƃ��ł���B
�̂Ƃ��ł���B
 �`
�` �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@
�@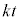 �@�@
�@�@ �@
�@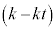 �@�@
�@�@ �@
�@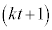
 �@
�@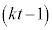 �@�@
�@�@ �@
�@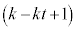 �@�@
�@�@ �@
�@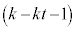
�ȉ��A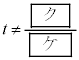 �Ƃ��A
�Ƃ��A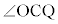 �����p�ł���Ƃ���B
�����p�ł���Ƃ���B
(2) 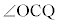 �����p�ł��邱�Ƃɂ��A(1)��k��
�����p�ł��邱�Ƃɂ��A(1)��k�� 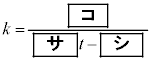 �@����A
�@����A�ƂȂ邱�Ƃ��킩��B
���ʂ��璼��OA�������������́A����OA�����ɓ�̕����ɕ�������B���̂����A�_B���܂ޕ�����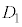 �C�܂܂Ȃ�������
�C�܂܂Ȃ�������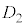 �Ƃ���B�܂��A���ʂ��璼��OB�������������́A����OB�����ɓ�̕����ɕ�������B���̂����A�_A���܂ޕ�����
�Ƃ���B�܂��A���ʂ��璼��OB�������������́A����OB�����ɓ�̕����ɕ�������B���̂����A�_A���܂ޕ�����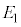 �C�܂܂Ȃ�������
�C�܂܂Ȃ�������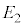 �Ƃ���B
�Ƃ���B �E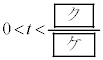 �Ȃ�A�_Q��
�Ȃ�A�_Q�� �B
�B �E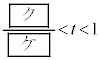 �Ȃ�A�_Q��
�Ȃ�A�_Q��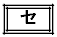 �B
�B  �C
�C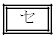 �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@
�@ �Ɋ܂܂�A����
�Ɋ܂܂�A����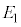 �Ɋ܂܂��B
�Ɋ܂܂��B
 �@
�@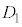 �Ɋ܂܂�A����
�Ɋ܂܂�A����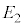 �Ɋ܂܂��B
�Ɋ܂܂��B
 �@
�@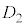 �Ɋ܂܂�A����
�Ɋ܂܂�A����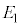 �Ɋ܂܂��B
�Ɋ܂܂��B
 �@
�@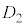 �Ɋ܂܂�A����
�Ɋ܂܂�A����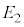 �Ɋ܂܂��B
�Ɋ܂܂��B
(3) ���Y����ƉԎq����́A�_P�̈ʒu��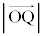 �̊W�ɂ��čl���Ă���B
�̊W�ɂ��čl���Ă���B 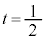 �̂Ƃ��A�@�ƇA�ɂ��A
�̂Ƃ��A�@�ƇA�ɂ��A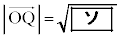 �Ƃ킩��B
�Ƃ킩��B
���Y�F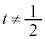 �̂Ƃ��ɂ��A
�̂Ƃ��ɂ��A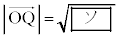 �ƂȂ�ꍇ�����邩�ȁB
�ƂȂ�ꍇ�����邩�ȁB �Ԏq�F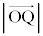 ��t ��p���ĕ\���āA
��t ��p���ĕ\���āA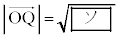 ����t �̒l�ɂ��čl��������Ǝv����B
����t �̒l�ɂ��čl��������Ǝv����B ���Y�F�v�Z����ς������ˁB
�Ԏq�F����OA�Ɋւ��āA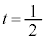 �̂Ƃ��̓_Q�ƑΏ̂ȓ_��R�Ƃ�����A
�̂Ƃ��̓_Q�ƑΏ̂ȓ_��R�Ƃ�����A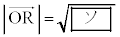 �ƂȂ��B
�ƂȂ��B ���Y�F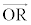 ��
��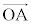 ��
��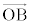 ��p���ĕ\�����Ƃ��ł���At �̒l�����߂�ꂻ�����ˁB
��p���ĕ\�����Ƃ��ł���At �̒l�����߂�ꂻ�����ˁB ����OA�Ɋւ��āA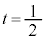 �̂Ƃ��̓_Q�ƑΏ̂ȓ_��R�Ƃ����
�̂Ƃ��̓_Q�ƑΏ̂ȓ_��R�Ƃ����
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ʃx�N�g���Ƃ��ẮA�L�͈͂Ƀe�X�g���悤�Ƃ������ƂŁA2�������Ɣ�ׂ�ƕp�o�Ƃ͌����Ȃ����e�ɂȂ��Ă��܂��B[�^]�ȍ~�́A�o��̈Ӑ}�𐳂����������ĉ����Ȃ��ƍ������܂��B
A�CB�͓_O�𒆐S�Ƃ��锼�a1�̉~����̓_�Ȃ̂ŁA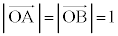 �@����B
�@����B
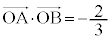 �@����C
�@����C
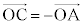 �@����D�@���AAC�͉~�̒��a�ł��B
�@����D�@���AAC�͉~�̒��a�ł��B
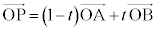 (
(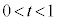 )�@����E
)�@����E
�A�C�@�|2�@�E�@3 ......[��]
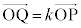 (k�F����)
(k�F����)�B���A
�G�@1�@�I�@0 ......[��]
�@�C�D���A
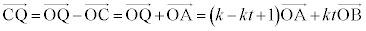 �@����F
�@����F�J�@4�@�L�@0 ......[��]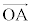 ��
��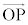 �������Ȃ̂ŁA�B�C�C�C�E���A
�������Ȃ̂ŁA�B�C�C�C�E���A �N�@3�@�P�@5 ......[��]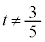 �ŁA
�ŁA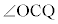 �����p�ł��邱�Ƃɂ��
�����p�ł��邱�Ƃɂ��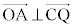 �A�F�ŁA�@�C�C��p���āA
�A�F�ŁA�@�C�C��p���āA �� 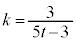 �@����A
�@����A �R�@3�@�T�@5�@�V�@3 ......[��]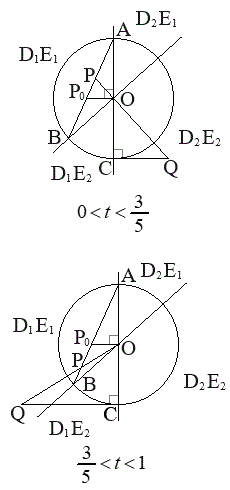
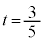 �̂Ƃ���P�C�܂�E���A
�̂Ƃ���P�C�܂�E���A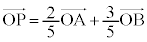 �ƂȂ�Ƃ���P��
�ƂȂ�Ƃ���P��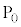 �Ƃ��܂��BP�́A
�Ƃ��܂��BP�́A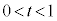 �ł���A����AB��̓_�ł���A
�ł���A����AB��̓_�ł���A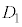 �C
�C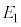 �Ɋ܂܂�܂��B
�Ɋ܂܂�܂��B �E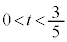 �Ȃ�A�A���A
�Ȃ�A�A���A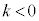 �ł��B���̂Ƃ�Q�́A����OP���O�Ɋւ���P�Ɣ��Α��ɂ���A����OA�Ɋւ���B�Ɣ��Α��A����OB�Ɋւ���A�Ɣ��Α��̓_�ŁA
�ł��B���̂Ƃ�Q�́A����OP���O�Ɋւ���P�Ɣ��Α��ɂ���A����OA�Ɋւ���B�Ɣ��Α��A����OB�Ɋւ���A�Ɣ��Α��̓_�ŁA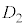 �Ɋ܂܂�A����
�Ɋ܂܂�A����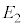 �Ɋ܂܂��_�ł��B
�Ɋ܂܂��_�ł��B �E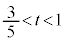 �Ȃ�A�A���A
�Ȃ�A�A���A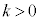 �ł��B���̂Ƃ�Q�́A����OP���O�Ɋւ���P�Ɠ������ɂ���A����OA�Ɋւ���B�Ɠ������A����OB�Ɋւ���A�Ɠ������̓_�ŁA
�ł��B���̂Ƃ�Q�́A����OP���O�Ɋւ���P�Ɠ������ɂ���A����OA�Ɋւ���B�Ɠ������A����OB�Ɋւ���A�Ɠ������̓_�ŁA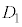 �Ɋ܂܂�A����
�Ɋ܂܂�A����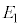 �Ɋ܂܂��_�ł��B
�Ɋ܂܂��_�ł��B 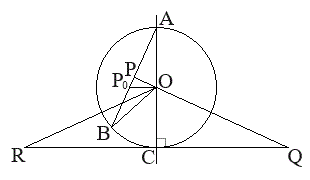 (3)
(3) 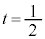 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A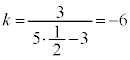 �C�E���A
�C�E���A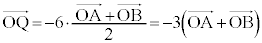 �@����G
�@����G�B�C�C���A
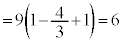 �@��
�@�� 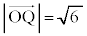
�\�@6 ......[��]����OA�Ɋւ��āA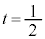 �̂Ƃ��̓_Q�ƑΏ̂ȓ_��R�Ƃ���ƁA
�̂Ƃ��̓_Q�ƑΏ̂ȓ_��R�Ƃ���ƁA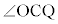 �͒��p�Ȃ̂ŁAQ��R�̒��_��C�ł��B����āA�D�C�G���A
�͒��p�Ȃ̂ŁAQ��R�̒��_��C�ł��B����āA�D�C�G���A �^�@�|�@�`�@2�@�c�@3 .......[��]
�D���A
���̂Ƃ��A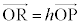 �ƂȂ钼��AB��̓_��P�Ƃ��āA�E���A
�ƂȂ钼��AB��̓_��P�Ƃ��āA�E���A ����āA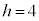 �C
�C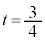
�e�@3�@�g�@4 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 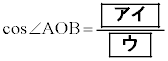 �ł���B
�ł���B �̂Ƃ��ł���B
�̂Ƃ��ł���B �Ƃ��A
�Ƃ��A �@����A
�@����A �Ȃ�A�_Q��
�Ȃ�A�_Q�� �Ȃ�A�_Q��
�Ȃ�A�_Q�� �ł���B
�ł���B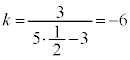 �C�E���A
�C�E���A