�@���ʃe�X�g���wIIB '23�N��5��@
�O�p��PABC�ɂ����āA��BC�̒��_��M�Ƃ����B�܂��A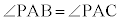 �Ƃ��A���̊p�x��θ�Ƃ����B�������A
�Ƃ��A���̊p�x��θ�Ƃ����B�������A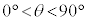 �Ƃ���B
�Ƃ���B
(1) 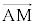 ��
�� �ƕ\����B�܂��A
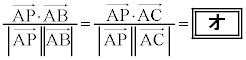 �@����@
�@����@�ł���B
 �̉Q
�̉Q  �@
�@ �@�@
�@�@ �@
�@ �@�@
�@�@ �@
�@
 �@
�@ �@�@
�@�@ �@
�@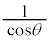 �@�@
�@�@ �@
�@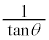
 �@
�@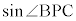 �@�@
�@�@ �@
�@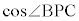 �@�@
�@�@ �@
�@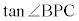
(2) 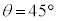 �Ƃ��A�����
�Ƃ��A����� �����藧�ꍇ���l����B���̂Ƃ�
�ł���B����ɁA����AM��̓_D��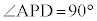 �����Ă���Ƃ���B���̂Ƃ��A
�����Ă���Ƃ���B���̂Ƃ��A �ł���B
�ł���B
(3) 
�Œ�܂�_��Q�Ƃ����B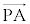 ��
��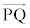 �������ł���O�p��PABC�͂ǂ̂悤�Ȃ��̂��ɂ��čl���悤�B�Ⴆ��(2)�̏ꍇ�ł́A�_Q�͓_D�ƈ�v���A
�������ł���O�p��PABC�͂ǂ̂悤�Ȃ��̂��ɂ��čl���悤�B�Ⴆ��(2)�̏ꍇ�ł́A�_Q�͓_D�ƈ�v���A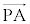 ��
��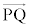 �͐����ł���B
�͐����ł���B
(i) 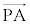 ��
��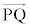 �������ł���Ƃ��A
�������ł���Ƃ��A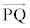 ��
��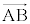 �C
�C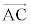 �C
�C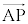 ��p���ĕ\���čl����ƁA
��p���ĕ\���čl����ƁA �����藧�B����ɇ@�ɒ��ӂ���ƁA
�����藧�B����ɇ@�ɒ��ӂ���ƁA ����
���� �����藧���Ƃ��킩��B
�����藧���Ƃ��킩��B ���������āA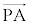 ��
��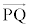 �������ł���A
�������ł���A �����藧�B�t��
�����藧�B�t�� �����藧�ĂA
�����藧�ĂA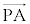 ��
��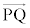 �͐����ł���B
�͐����ł���B
 �̉Q
�̉Q  �̉Q
�̉Q
(ii) k�𐳂̒萔�Ƃ�
�����藧�Ƃ���B���̂Ƃ��A �����藧�B
�����藧�B
�܂��A�_B���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��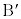 �Ƃ��A���l�ɓ_C���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��
�Ƃ��A���l�ɓ_C���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��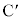 �Ƃ���B
�Ƃ���B
���̂Ƃ��A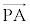 ��
��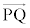 �������ł��邱�Ƃ́A
�������ł��邱�Ƃ́A �ł��邱�ƂƓ��l�ł���B����
�ł��邱�ƂƓ��l�ł���B����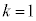 �̂Ƃ��A
�̂Ƃ��A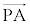 ��
��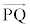 �������ł��邱�Ƃ́A
�������ł��邱�Ƃ́A �ł��邱�ƂƓ��l�ł���B
�ł��邱�ƂƓ��l�ł���B
 �̉Q
�̉Q 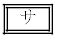 �̉Q
�̉Q �@
�@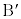 ��
��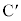 ������AP�����ꂼ��
������AP�����ꂼ��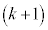 �F1��1�F
�F1��1�F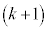 �ɓ�������_
�ɓ�������_ �@
�@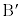 ��
��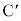 ������AP�����ꂼ��1�F
������AP�����ꂼ��1�F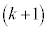 ��
��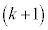 �F1�ɓ�������_
�F1�ɓ�������_ �@
�@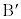 ��
��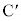 ������AP�����ꂼ��k�F1��1�Fk�ɓ�������_
������AP�����ꂼ��k�F1��1�Fk�ɓ�������_ �@
�@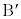 ��
��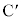 ������AP�����ꂼ��1�Fk��k�F1�ɓ�������_
������AP�����ꂼ��1�Fk��k�F1�ɓ�������_ �@
�@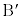 ��
��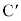 ���Ƃ��ɐ���AP��k�F1�ɓ�������_
���Ƃ��ɐ���AP��k�F1�ɓ�������_ �@
�@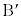 ��
��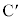 ���Ƃ��ɐ���AP��1�Fk�ɓ�������_
���Ƃ��ɐ���AP��1�Fk�ɓ�������_ �̉Q
�̉Q �@��PAB�Ɓ�PAC���Ƃ��ɐ��O�p�`
�@��PAB�Ɓ�PAC���Ƃ��ɐ��O�p�` �@��PAB�Ɓ�PAC�����ꂼ��
�@��PAB�Ɓ�PAC�����ꂼ��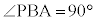 �C
�C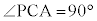 �������p�ӎO�p�`
�������p�ӎO�p�` �@��PAB�Ɓ�PAC�����ꂼ��
�@��PAB�Ɓ�PAC�����ꂼ��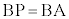 �C
�C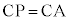 �����ӎO�p�`
�����ӎO�p�` �@��PAB�Ɓ�PAC������
�@��PAB�Ɓ�PAC������ �@
�@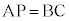
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�ɏ�����Ă���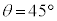 �C
�C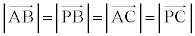 ��(3)�ɂ��y��ł���ƍ��o����ƍs���l�܂�܂��B�[���l�����܂��ɗ���ɏ���Đi�߂�����ǂ������ł��B�Ō�̃V�����s���Ȃ̂ŁA�����@�ʼn��܂��傤�B�K�v�������l����Ɖ�2����悤�Ɍ����܂����A�t���m���߂�K�v������܂��B
��(3)�ɂ��y��ł���ƍ��o����ƍs���l�܂�܂��B�[���l�����܂��ɗ���ɏ���Đi�߂�����ǂ������ł��B�Ō�̃V�����s���Ȃ̂ŁA�����@�ʼn��܂��傤�B�K�v�������l����Ɖ�2����悤�Ɍ����܂����A�t���m���߂�K�v������܂��B
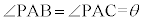 �C����сA�����̒�`���A
�C����сA�����̒�`���A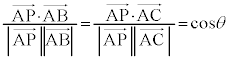 �@����@�@�I 1 ......[��]
�@����@�@�I 1 ......[��]
(2) �@���A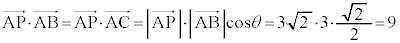 �@�J 9 ......[��]
�@�J 9 ......[��] 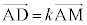 �Ƃ����ƁA�J�C(1)�̌��ʂ�p���āA
�Ƃ����ƁA�J�C(1)�̌��ʂ�p���āA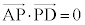 ���A
���A
(3) �����ł́A��ABP����ACP�����p�ӎO�p�`�ł͂Ȃ��A�܂�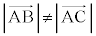 �Ƃ��čl���܂��B�_Q���A
�Ƃ��čl���܂��B�_Q���A �Œ�߂�ƁAM����BC�̒��_�ł��邱�Ƃ���A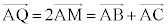
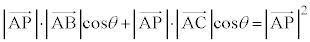 ��
�� 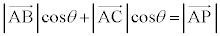 �@�P 3 ......[��]
�@�P 3 ......[��]�ȏ���A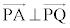 ��
�� 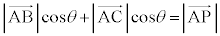 �@����A�@(�t�̐����͖�蕶�ɏ�����Ă��܂�)
�@����A�@(�t�̐����͖�蕶�ɏ�����Ă��܂�)
(ii) 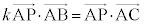 ���A
���A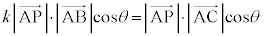 �C����āA
�C����āA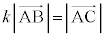 �@�R 0 ......[��]
�@�R 0 ......[��] 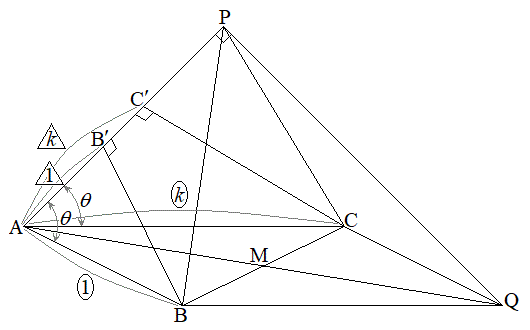 �_B���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��
�_B���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��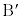 �Ƃ��A���l�ɓ_C���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��
�Ƃ��A���l�ɓ_C���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��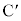 �Ƃ����(�E�}�Q��)�A
�Ƃ����(�E�}�Q��)�A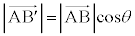 �C
�C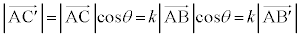
�A�ɑ������ƁA
������A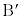 ��AP��1�Fk�ɓ�������_(�x�N�g���̓����E�O�����Q��)�ł��B
��AP��1�Fk�ɓ�������_(�x�N�g���̓����E�O�����Q��)�ł��B
�܂��A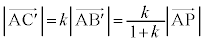 �C
�C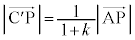 �@����C
�@����C
������A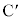 ��AP��k�F1�ɓ�������_�ł��B�@�T 4 ......[��]�t�ɃT��
��AP��k�F1�ɓ�������_�ł��B�@�T 4 ......[��]�t�ɃT�� �����藧�Ƃ��A�B�C�C����������̂ŁA
�����藧�Ƃ��A�B�C�C����������̂ŁA �ƂȂ�A����������̂ŁA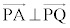 �� �T��
�� �T��
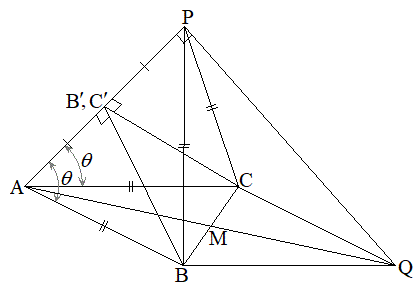
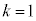 �̂Ƃ��A
�̂Ƃ��A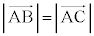 �܂�
�܂�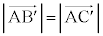 (
(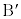 ��
��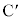 ������̓_)�ƂȂ�܂�(�E�}�Q��)���A�ꌩ����ƁA�K����I�������Ȃ��悤�Ɍ����܂��B�����ŁA�����@�ōl���܂��B
������̓_)�ƂȂ�܂�(�E�}�Q��)���A�ꌩ����ƁA�K����I�������Ȃ��悤�Ɍ����܂��B�����ŁA�����@�ōl���܂��B
�܂��A��PAB�Ɓ�PAC�����O�p�`�Ƃ͌����Ȃ��̂ŁA �͏��O���܂��B
�͏��O���܂��B
�u��L����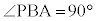 �C
�C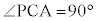 �v�Ƃ͌����Ȃ��̂ŁA
�v�Ƃ͌����Ȃ��̂ŁA �����O���܂��B
�����O���܂��B
�܂��A�u��L����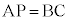 �v�Ƃ������Ȃ��̂ŁA
�v�Ƃ������Ȃ��̂ŁA �����O����܂��BB�CC���璼��AP�ɉ��낵�������̑�����v����AP�̒��_�ɂȂ�̂ŁA
�����O����܂��BB�CC���璼��AP�ɉ��낵�������̑�����v����AP�̒��_�ɂȂ�̂ŁA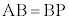 (B��AP�̐���������̓_)�C
(B��AP�̐���������̓_)�C (C��AP�̐���������̓_)�ł���A��PAB�Ɓ�PAC�͂Ƃ��ɓӎO�p�`�ł��B�t�ɁA
(C��AP�̐���������̓_)�ł���A��PAB�Ɓ�PAC�͂Ƃ��ɓӎO�p�`�ł��B�t�ɁA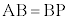 �C
�C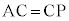 �ł���A
�ł���A ���A����������̂ŁA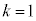 �܂�
�܂�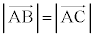 �̂Ƃ��A
�̂Ƃ��A ��
��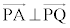 �Ɠ��l�ł��B
�Ɠ��l�ł��B
 �̂Ƃ��A��PAB �� ��PAC�ł����A��PAB �� ��PAC�ł����Ă��A��PAB�Ɓ�PAC���ӎO�p�`�Ƃ͌��炸�A
�̂Ƃ��A��PAB �� ��PAC�ł����A��PAB �� ��PAC�ł����Ă��A��PAB�Ɓ�PAC���ӎO�p�`�Ƃ͌��炸�A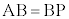 �C
�C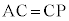 �Ƃ͌����Ȃ��̂ŇA���������A
�Ƃ͌����Ȃ��̂ŇA���������A ��
��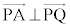 �Ɠ��l�ł͂���܂���(�����E�������Q��)�B�@�V 2 ......[��]
�Ɠ��l�ł͂���܂���(�����E�������Q��)�B�@�V 2 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 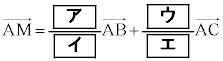
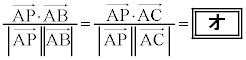 �@����@
�@����@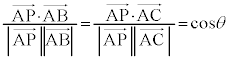 �@����@�@�I 1 ......[��]
�@����@�@�I 1 ......[��]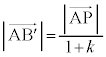 �C
�C