��s�嗝�n���w'07�N�O��[3]
�ȉ��̖₢�ɓ�����B
(1) ����a�Cb�Cx�Cy�ɑ��āA�s����
�����藧���Ƃ������B
(2) �����𐬕��Ƃ���2���̐����s��A�ɂ��āA����2�̖���(�A)��(�C)�͓��l�ł��邱�Ƃ��ؖ�����B
(�A)�@�s��A�͋t�s�������
(�C)�@����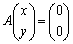 ���݂�������x�Cy��
���݂�������x�Cy��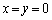 �Ɍ���B
�Ɍ���B (3) ����a�Cb�Cc�Cd��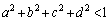 ���݂����Ƃ��A�s��
���݂����Ƃ��A�s�� 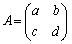 �C
�C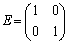
�ɑ��āA�s��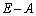 �͋t�s��������Ƃ������B
�͋t�s��������Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�̓R�[�V�[�E�V�������c�̕s�����ł�(�s�����̏ؖ����Q��)�B
�s��A���t�s�������݂��邩�ǂ����A�Ƃ������Ƃׂ�Ƃ��ɁA
�E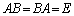 ���݂���B��T��
���݂���B��T�� �E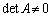 ������
������ �́A2�ʂ�̃A�v���[�`�̎d��������܂��B���̖��ł́A��҂ōl���܂��B
(1) 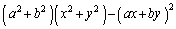
�� 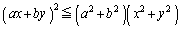
(2) �u(�A)��(�C)�����l�v�Ƃ����̂́A(�A)��(�C)�����݂��K�v�\�������ɂȂ��Ă��āA(�A)��(�C)��(�C)��(�A)���Ƃ��ɐ��藧�A�Ƃ������Ƃł��B �E(�A)��(�C)�������܂��B
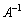 �����݂���Ƃ��A����
�����݂���Ƃ��A����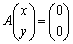 �̍�����
�̍�����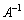 �������āA
�������āA����āA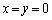 �Ɍ����܂��B
�Ɍ����܂��B �E(�C)��(�A)���A�w���@�ɂ���Ď����܂��B (�C)�����藧�Ƃ��A �C
�C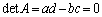 �Ɖ��肵�܂��B
�Ɖ��肵�܂��B (i) 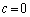 �Ȃ�A
�Ȃ�A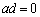 ���a�Cd�̂ǂ��炩��0�ł��B
���a�Cd�̂ǂ��炩��0�ł��B 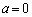 �Ȃ�A����
�Ȃ�A����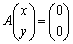 �́A
�́A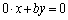 �C
�C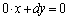
x�͔C�ӂ̎����ł悢���ƂɂȂ�A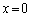 �Ɍ����邱�Ƃɔ����܂��B
�Ɍ����邱�Ƃɔ����܂��B
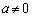 �C
�C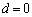 �Ȃ�A����
�Ȃ�A����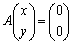 �́A
�́A 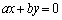 �C
�C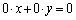
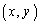 �͒���
�͒���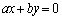 ��̔C�ӂ̓_�ł悢���ƂɂȂ�A
��̔C�ӂ̓_�ł悢���ƂɂȂ�A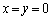 �Ɍ����邱�Ƃɔ����܂��B
�Ɍ����邱�Ƃɔ����܂��B(ii) 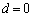 �Ȃ�A
�Ȃ�A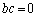 ���b�Cc�̂ǂ��炩��0�ł��B
���b�Cc�̂ǂ��炩��0�ł��B 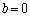 �Ȃ�A����
�Ȃ�A����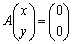 �́A
�́A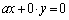 �C
�C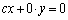
y�͔C�ӂ̎����ł悢���ƂɂȂ�A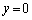 �Ɍ����邱�Ƃɔ����܂��B
�Ɍ����邱�Ƃɔ����܂��B
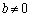 �C
�C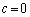 �Ȃ�A����
�Ȃ�A����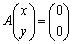 �́A
�́A 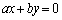 �C
�C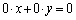
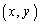 �͒���
�͒���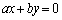 ��̔C�ӂ̓_�ł悢���ƂɂȂ�A
��̔C�ӂ̓_�ł悢���ƂɂȂ�A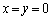 �Ɍ����邱�Ƃɔ����܂��B
�Ɍ����邱�Ƃɔ����܂��B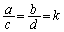 (k�F����)�Ƃ����ƁA����
(k�F����)�Ƃ����ƁA����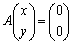 �́A
�́A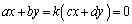 �C
�C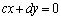
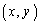 �͒���
�͒���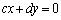 ��̔C�ӂ̓_�ł悢���ƂɂȂ�A
��̔C�ӂ̓_�ł悢���ƂɂȂ�A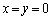 �Ɍ����邱�Ƃɔ����܂��B
�Ɍ����邱�Ƃɔ����܂��B�ȏ���A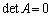 �Ƃ�������͌��ł���A
�Ƃ�������͌��ł���A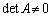 �C����āA�s��A�͋t�s��������܂��B
�C����āA�s��A�͋t�s��������܂��B �� (�A) �� (�C)
(3) 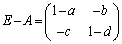 ���t�s��������Ƃ��������߂ɂ́A
���t�s��������Ƃ��������߂ɂ́A ��������悢�킯�ł����A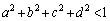 �Ƃ������������킹�āA
�Ƃ������������킹�āA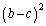 �̂悤�Ȍ`����邽�߂ɁA
�̂悤�Ȍ`����邽�߂ɁA ���l���Ă݂܂��B
�� 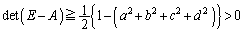 ����āA
����āA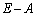 �͋t�s��������܂��B�ʉ��@��L�̉ł́A����Ă݂�����R���܂��s�����A�Ƃ����ʂ�����܂����A���̗���ɉ�����(1)�C(2)�𗘗p���ĉ���̂ł���A
�͋t�s��������܂��B�ʉ��@��L�̉ł́A����Ă݂�����R���܂��s�����A�Ƃ����ʂ�����܂����A���̗���ɉ�����(1)�C(2)�𗘗p���ĉ���̂ł���A 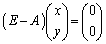 �@����@
�@����@���݂���x�Cy���ǂ�Ȏ��������l���邱�ƂɂȂ�܂��B
�@�́A
�ƂȂ�܂����A������(1)�̌��ʂ��g���ƁA
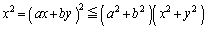 �@����A
�@����A
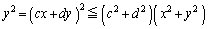 �@����B
�@����B�A�{�B���A
�����ŁA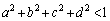 �Ȃ̂ŁA
�Ȃ̂ŁA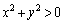 �ł���A
�ł���A �Ƃ������ƂɂȂ��Ă��܂��܂��B
�]���āA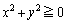 �Ȃ̂�
�Ȃ̂�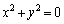 �C�܂�A�@���݂���x�Cy��
�C�܂�A�@���݂���x�Cy��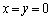 �Ɍ����邱�ƂɂȂ�܂��B
�Ɍ����邱�ƂɂȂ�܂��B
����āA(2)���A �͋t�s��������܂��B
�͋t�s��������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B