�H�c��㐔�w'08�N[1]
����m�ɑ��A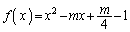 �Ƃ����B���̖₢�ɓ�����B
�Ƃ����B���̖₢�ɓ�����B
(1) ������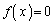 ���A�����̉������Ȃ��Ƃ�1���悤��m�̒l�����߂�B
���A�����̉������Ȃ��Ƃ�1���悤��m�̒l�����߂�B (2) �s����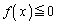 ��������x���A���傤��4����悤��m�̒l�����߂�B
��������x���A���傤��4����悤��m�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�{��̂悤�ȁA���Ăǂ��Ȃ�������肪�A������ł͂�����������m��܂���B
(1) �������F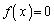 ��2����p�Cq�Ƃ��Ap�𐮐����Ƃ��܂��B
��2����p�Cq�Ƃ��Ap�𐮐����Ƃ��܂��B 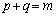 �@����@
�@����@
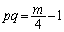 �@����A
�@����A�@���Am�͐����Ȃ̂ŁAp�������Ȃ�q�������ł����āA2���͂Ƃ��ɐ����A�Ƃ������ƂɂȂ�܂��B
����ƁA�A���A
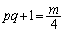 �@����B
�@����B�ƂȂ�A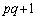 �͐����Ȃ̂ŁA��ӂ��݂������߂ɂ́Am��4�̔{���ɂȂ邱�Ƃ��K�v���Ƃ킩��܂��B
�͐����Ȃ̂ŁA��ӂ��݂������߂ɂ́Am��4�̔{���ɂȂ邱�Ƃ��K�v���Ƃ킩��܂��B
�@���A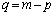 �C������B�ɑ������ƁA
�C������B�ɑ������ƁA 4�������āA
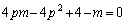 �@����C
�@����C���������`���o�Ă�����A(����A)�~(����B)��(����C)�̌`����邱�Ƃ�ڎw���܂��B�܂��͇C���ӂ̈������������݂܂��B�{��̂悤�Ȗ��ł́A���ʂ͈��������ł��Ȃ��̂ł����A���̂Ƃ��A���������ł����ɂ��Ԃ�Ă��܂��������A�����̒萔�ɂȂ�悤�ɍH�v���܂��B
�܂��A
�ɖڂ�t���܂��B�c��́A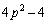 �ł����A��������
�ł����A��������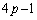 ���Ђ˂肾���̂ł��B
���Ђ˂肾���̂ł��B �Ȃ̂ŁA�C���A
�ƕό`���܂��B4�������č��ӂ�15�������c���ƁA
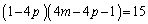 �@����D
�@����D����ŁA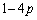 �C
�C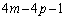 �͐����Ȃ̂ŁA
�͐����Ȃ̂ŁA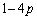 ��15�̖ł����āA
��15�̖ł����āA �Ɍ����܂��B
���̂���p�������ɂȂ�̂́A
�̂Ƃ��݂̂ł��B
(i) 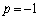 �̂Ƃ��A�D�́A
�̂Ƃ��A�D�́A 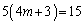 ��
�� 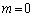
(ii) 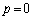 �̂Ƃ��A�D�́A
�̂Ƃ��A�D�́A 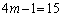 ��
�� 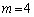
(iii) 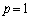 �̂Ƃ��A�D�́A
�̂Ƃ��A�D�́A 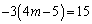 ��
�� 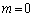
(iv) 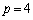 �̂Ƃ��A�D�́A
�̂Ƃ��A�D�́A 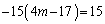 ��
�� 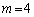
�܂�A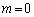 �̂Ƃ��A2���́A
�̂Ƃ��A2���́A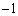 ��1�C
��1�C
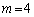 �̂Ƃ��A2���́A0��4�ɂȂ�܂��B
�̂Ƃ��A2���́A0��4�ɂȂ�܂��B
����āA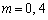 ......[��]�@(m�͊m����4�̔{���ɂȂ��Ă��܂�)
......[��]�@(m�͊m����4�̔{���ɂȂ��Ă��܂�)
(2) �܂��A
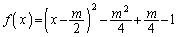 �@����E
�@����E���A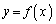 �̃O���t�́A���F
�̃O���t�́A���F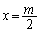 �Ɋւ��đΏ̂ł��B����F�@(2�������Q��)
�Ɋւ��đΏ̂ł��B����F�@(2�������Q��) 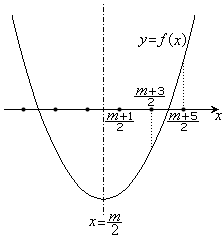 ���A�������F
���A�������F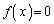 �́A���قȂ�2�������������Aa�������Ƃ��āA�F���A
�́A���قȂ�2�������������Aa�������Ƃ��āA�F���A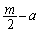 �����Ȃ�
�����Ȃ�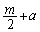 �����ł��B���̂Ƃ��A
�����ł��B���̂Ƃ��A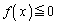 ���݂���x�͈̔͂́A
���݂���x�͈̔͂́A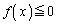 ��������x���A���傤��4����A�Ƃ������Ƃ́A
��������x���A���傤��4����A�Ƃ������Ƃ́A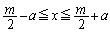 �͈̔͂ɐ��������傤��4����A�Ƃ������Ƃł��Bm���������Ƃ��܂��B
�͈̔͂ɐ��������傤��4����A�Ƃ������Ƃł��Bm���������Ƃ��܂��B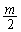 �͐����ł��B���̂Ƃ��A�F���Ak�𐮐��Ƃ��āA
�͐����ł��B���̂Ƃ��A�F���Ak�𐮐��Ƃ��āA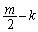 ���A
���A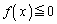 �����ŏ��̐������Ƃ���ƁA
�����ŏ��̐������Ƃ���ƁA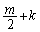 ���A
���A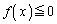 �����ő�̐����ɂȂ�܂��B���Ƃ���ƁA
�����ő�̐����ɂȂ�܂��B���Ƃ���ƁA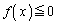 ���������́A
���������́A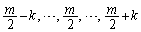 ��
��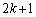 ���݂��邱�ƂɂȂ�A4�A�Ƃ������Ƃ͂��蓾�܂���B
���݂��邱�ƂɂȂ�A4�A�Ƃ������Ƃ͂��蓾�܂���B
�]����m�͊�ł��B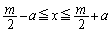 ����4�̐����́A
����4�̐����́A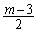 �C
�C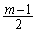 �C
�C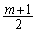 �C
�C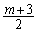 �Ƃ������ƂɂȂ�܂��B
�Ƃ������ƂɂȂ�܂��B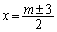 ��
��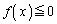 ���݂����܂����A
���݂����܂����A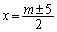 ��
��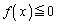 ���݂����܂���B
���݂����܂���B
�����Ȃ邽�߂̕K�v�\�������́A�F���A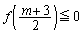 ����
���� 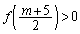
�ł��B�E���A
�� 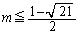 �C
�C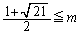 �@����G
�@����G
�E���A �� 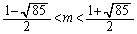 �@����H
�@����H
�G���H���A 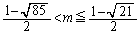 �C
�C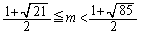 �@����I
�@����I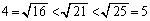 �C
�C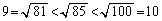 �ł��B
�ł��B
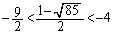 �C
�C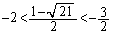 �C
�C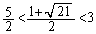 �C
�C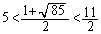 ���A�I���݂����m�́A
���A�I���݂����m�́A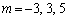 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B