�����吔�w'08�N[2]
n��2�ȏ�̎��R���Ƃ���B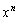 ��
��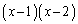 �Ŋ���������
�Ŋ���������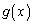 �C�]���
�C�]���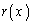 �Ƃ���B���̖₢�ɓ�����B
�Ƃ���B���̖₢�ɓ�����B
(1) 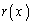 �����߂�B
�����߂�B (2) 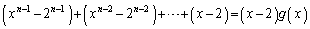 �����藧���Ƃ������B
�����藧���Ƃ������B (3) 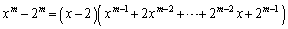 �@(m�͎��R��)�ł��邱�Ƃ�p���āA
�@(m�͎��R��)�ł��邱�Ƃ�p���āA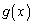 ��
��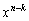 (
(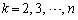 )�̌W�������߂�B
)�̌W�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������̏��Z�����䐔���̗Z�����ł��B
������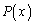 �𑽍���
�𑽍���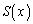 �Ŋ���A����
�Ŋ���A����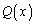 �C�]�肪
�C�]�肪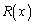 �ɂȂ�Ƃ��A
�ɂȂ�Ƃ��A
�܂��A�]��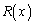 �̎�����
�̎�����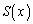 �̎�����菬�����Ȃ�܂��B
�̎�����菬�����Ȃ�܂��B
���ꂪ�������Ŏv�����Ȃ��Ƃ��́A
�̂Ƃ��A
�ƂȂ邱�Ƃ��l���܂��傤�B
(1) 2����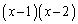 �Ŋ���̂ŗ]��
�Ŋ���̂ŗ]��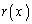 ��1�����܂��͒萔�ŁA
��1�����܂��͒萔�ŁA �Ƃ����܂��B������A
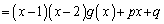 �@����@
�@����@�@�ɂ����āA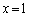 �Ƃ���ƁA
�Ƃ���ƁA 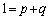 �@����A
�@����A�@�ɂ����āA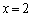 �Ƃ���ƁA
�Ƃ���ƁA 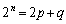 �@����B
�@����B�A�C�B��A������ƁA
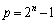 �C
�C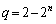
�� 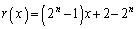 ......[��]
......[��]
(2) 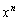 ��
��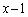 �Ŋ����ď���
�Ŋ����ď���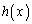 �C�]�肪�萔s�ɂȂ�Ƃ��܂��B
�C�]�肪�萔s�ɂȂ�Ƃ��܂��B 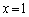 �Ƃ���ƁA
�Ƃ���ƁA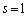
�� 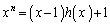 �@����C
�@����C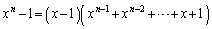
���A
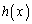 ��
��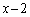 �Ŋ����ď���
�Ŋ����ď���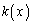 �ɂȂ�Ƃ��āA�]��́A��]�̒藝���A
�ɂȂ�Ƃ��āA�]��́A��]�̒藝���A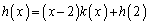 �@����D
�@����D���A�C�ɑ������ƁA
����́A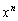 ��
��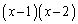 �Ŋ���ƁA����
�Ŋ���ƁA����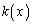 �C�]�肪
�C�]�肪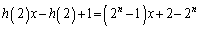 �ɂȂ邱�Ƃ��Ӗ����܂��B�܂�A
�ɂȂ邱�Ƃ��Ӗ����܂��B�܂�A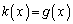 �ł��B
�ł��B
�D���A �ʉ��D(1)�̌��ʂ��A
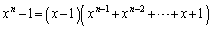 ��p����ƁA
��p����ƁA�� 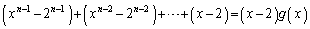
(3) ��蕶�̓������A
������
�ӁX�������킹��ƁA
(2)�Ŏ�����������p����ƁA
������A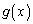 ��
��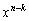 (
(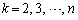 )�̌W���́A
)�̌W���́A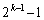 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B