��H���w'08�N[4]
���R��n�Ǝ���x�ɑ���
�Ƃ����B�ȉ��̖₢�ɓ�����B
(1)  �̂Ƃ��A�Ɍ��l
�̂Ƃ��A�Ɍ��l �����߂�B
�����߂�B (2) ���ׂĂ̎���x�ɑ��āA �����݂��邱�Ƃ������B�܂��A
�����݂��邱�Ƃ������B�܂��A �Ƃ����Ƃ��Ag��x��p���ĕ\���B
�Ƃ����Ƃ��Ag��x��p���ĕ\���B (3) x�̒l�����ׂĂ̎�����ω�����Ƃ��A(2)�Œ�܂���g�̍ő�l�ƍŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͖������䋉���ł��邱�ƂɋC�Â����邽�߂̃q���g�ɉ߂��Ȃ��̂ŁA(2)����n�߂邱�Ƃɂ��܂��B
�����r�Ƃ����ƁA
������Đ�������ƁA
 �@����@
�@����@x�����ׂĂ̎������Ƃ肤��Ƃ��āA�@��x��2���������ƌ���Ƃ������������̂ŁA���ʎ� �ɂ��āA
�ɂ��āA ��  ����āA
����āA ��薳�����䋉��
��薳�����䋉�� �͎������A
�͎������A �����݂��܂��B
�����݂��܂��B
��  ......[��]
......[��]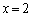 �̂Ƃ��A
�̂Ƃ��A ......[��]
......[��]
(3) (2)���A
������Đ�������ƁA
 �@����A
�@����Ax�����ׂĂ̎������Ƃ肤��Ƃ��āA�A��x��2���������ƌ���Ƃ������������̂ŁA���ʎ� �ɂ��āA
�ɂ��āA ��  �@(�����͇A���d�������ꍇ�ŁA
�@(�����͇A���d�������ꍇ�ŁA �̂Ƃ�
�̂Ƃ� �C
�C �̂Ƃ�
�̂Ƃ� )g�̍ő�l�F
)g�̍ő�l�F �C�ŏ��l�F0 ......[��]
�C�ŏ��l�F0 ......[��]
�NjL�D��L�ł�2���������𗘗p���ĉ��܂������A�������Ar��g�ɂ��ẮA�������Ē��ׂ邱�Ƃ��ł��܂��B
�����\�� ���Ag�̍ő�l�F
���Ag�̍ő�l�F �C�ŏ��l�F0�ƂȂ�܂��B
�C�ŏ��l�F0�ƂȂ�܂��B
���ǁA���̖��́A �Ƃ����`�̊��̋���(��X�̊��̃O���t���Q��)���e�[�}�ɂȂ��Ă���̂ł����A���l�̂��Ƃ��l������ɁA���H��'92�N�O��[1]�F
�Ƃ����`�̊��̋���(��X�̊��̃O���t���Q��)���e�[�}�ɂȂ��Ă���̂ł����A���l�̂��Ƃ��l������ɁA���H��'92�N�O��[1]�F x�̊� (
(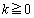 )��1�ȊO�̐����l���Ƃ�Ȃ��悤�Ȓ萔k�̒l�͈̔͂����߂�B
)��1�ȊO�̐����l���Ƃ�Ȃ��悤�Ȓ萔k�̒l�͈̔͂����߂�B ������܂��B������l���Ă݂܂��B
 ��1�ȊO�̐����l���Ƃ�Ȃ��̂ŁA
��1�ȊO�̐����l���Ƃ�Ȃ��̂ŁA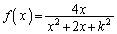 ��0�ȊO�̐����l���Ƃ�Ȃ����ƂɂȂ�܂��B
��0�ȊO�̐����l���Ƃ�Ȃ����ƂɂȂ�܂��B
 �̂Ƃ��A
�̂Ƃ��A �́A0�ȊO�̂��ׂĂ̐����l���Ƃ肤��̂ŕs�K�ł��B����āA
�́A0�ȊO�̂��ׂĂ̐����l���Ƃ肤��̂ŕs�K�ł��B����āA �ł��B
�ł��B
����F ��������p (
��������p ( )�����ꍇ�A
)�����ꍇ�A �ł���A
�ł���A �ɂ�����
�ɂ����� �͘A���Ȋ��ł��B
�͘A���Ȋ��ł��B
 ���������������Ȃ��ꍇ�́A���ׂĂ̎���x�ɂ�����
���������������Ȃ��ꍇ�́A���ׂĂ̎���x�ɂ����� �͘A���Ȋ��ł��B
�͘A���Ȋ��ł��B
�����ƁA �C
�C ���A
���A �ł��邱�Ƃ��K�v�\���ł��B
�ł��邱�Ƃ��K�v�\���ł��B ���݂�������x�����݂��Ȃ����߂̏������l���܂��B
������Đ�������ƁA
���ꂪ�������������Ȃ��̂ŁA
���ʎ��F
 ���A
���A �@����@
�@����@

���݂�������x�����݂��܂���B
������Đ�������ƁA���ꂪ�������������Ȃ��̂ŁA
���ʎ��F
 ���A
���A �@����A
�@����A
�@�C�A���A ......[��]�������A
......[��]�������A �̑����\�ׂ邱�Ƃ��ł��܂��B
�̑����\�ׂ邱�Ƃ��ł��܂��B�����\�� ���A
���A �ł��邽�߂ɂ́A
�ł��邽�߂ɂ́A 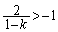 ����
���� 
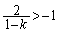 ���A
���A
��  �܂���
�܂���  �@����B
�@����B
 ���A
���A �@����C
�@����C
�B���C���A �ƂȂ�܂��B
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 

 ......[��]
......[��]
