�����w�|�吔�w'08�N[4]
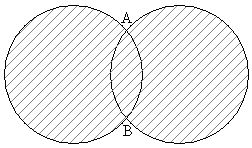 ���a1��2�̉~���}�̂悤�ɈقȂ�2�_�Ō�����Ă���B2�̌�_��A�CB�Ƃ��A��AB�ɑ���~�̒��S�p�̑傫����θ (
���a1��2�̉~���}�̂悤�ɈقȂ�2�_�Ō�����Ă���B2�̌�_��A�CB�Ƃ��A��AB�ɑ���~�̒��S�p�̑傫����θ (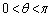 )�Ƃ���B�ΐ��������}�`��D�Ƃ��AD�̎��͂̒�����L�CD�̖ʐς�S�Ƃ���B
)�Ƃ���B�ΐ��������}�`��D�Ƃ��AD�̎��͂̒�����L�CD�̖ʐς�S�Ƃ���B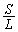 ���ő�ɂ���θ ������1���݂��邱�Ƃ������B
���ő�ɂ���θ ������1���݂��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��
�Z�����̌�AB�̒�����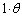 (��ʊp���Q��)�C�������̌�AB�̒����́A�~��
(��ʊp���Q��)�C�������̌�AB�̒����́A�~��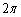 ����θ �������āA
����θ �������āA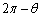 �C����āA����2���́A
�C����āA����2���́A
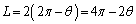 �@����@
�@����@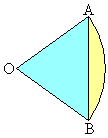 ��AB�ƒZ�����̌�AB�ň͂܂�镔���̖ʐς́A��`OAB����O�p�`OAB�̖ʐς������āA
��AB�ƒZ�����̌�AB�ň͂܂�镔���̖ʐς́A��`OAB����O�p�`OAB�̖ʐς������āA
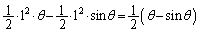 �@����A
�@����A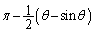 �C����āA����2���́A
�C����āA����2���́A
�� 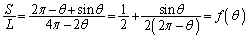
������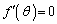 �Ƃ��Ă�θ �����߂邱�Ƃ��ł�����������܂���B
�Ƃ��Ă�θ �����߂邱�Ƃ��ł�����������܂���B
�����ŁA���q�������o���āAθ �ɂ���Ăǂ̂悤�ɕω����邩���ׂĂ݂܂��B���q���A
�Ƃ����܂��B
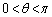 �ɂ����āA
�ɂ����āA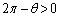 �C
�C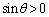 ���A
���A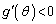 �ŁA
�ŁA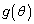 �͒P�������ł��Bθ �ɒl������
�͒P�������ł��Bθ �ɒl������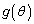 �̒l���v�Z���Ă݂�ƁA
�̒l���v�Z���Ă݂�ƁA
�ƂȂ��Ă���̂ŁA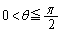 �ɂ����Ă�
�ɂ����Ă�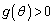 �C�܂��A
�C�܂��A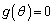 ��
��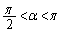 �͈̔͂ɂ���1�̉�α�������܂��B
�͈̔͂ɂ���1�̉�α�������܂��B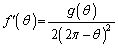 ���A
���A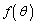 �ɂ��Ď��̑����\�������܂�(���̑������Q��)�B
�ɂ��Ď��̑����\�������܂�(���̑������Q��)�B
�����\���A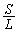 ���ő�ɂ���θ ������1���݂��܂��B
���ő�ɂ���θ ������1���݂��܂��B
�NjL�D�ő�ŏ��ׂ邽�߂ɓ��������߂Ă��A���������ꂢ�łȂ��A�Ƃ����ꍇ������܂��B�{��ł͕��q���o���Ē��ׂ邱�Ƃɂ��������܂����B���l�̋Z�I���g������ɁA��嗝'96���[2]�F
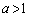 �ɑ��āA������
�ɑ��āA������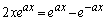 ���l����B
���l����B(1) ���̕������͐��̉�������1�����Ƃ������B
(2) ���̉���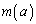 �Ƃ����Ƃ��A
�Ƃ����Ƃ��A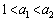 �Ȃ��
�Ȃ��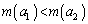 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (3) 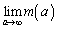 �����߂�B
�����߂�B
������܂��B������l���Ă݂܂��B
(1) ���̌`�̂܂܂ł͌������̂ŁA���ӂ�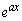 (
(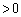 )�Ŋ���܂��B
)�Ŋ���܂��B 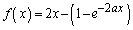 �Ƃ����ƁA
�Ƃ����ƁA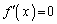 �Ƃ���ƁA
�Ƃ���ƁA���ӂ̑ΐ����l����ƁA
�� 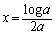 (
(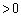 )
)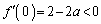 �C
�C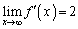 ���A�ȉ��̑����\�������܂��B
���A�ȉ��̑����\�������܂��B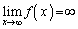 �C�܂��A�����\���
�C�܂��A�����\���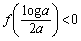 �ƂȂ�̂ŁA������
�ƂȂ�̂ŁA������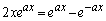 �C�܂�A
�C�܂�A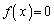 ��
��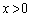 �͈̔͂ɂ���1�̉��������܂��B
�͈̔͂ɂ���1�̉��������܂��B (2) �e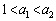 �Ȃ��
�Ȃ��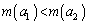 '�Ƃ������Ƃ́A
'�Ƃ������Ƃ́A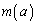 ��a�̑������Ƃ������Ƃł��B
��a�̑������Ƃ������Ƃł��B �]���āA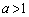 �ł����
�ł����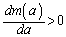 �ł��邱�Ƃ������悢�킯�ł��B
�ł��邱�Ƃ������悢�킯�ł��B
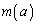 ��
��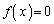 �̉��Ȃ̂ŁA
�̉��Ȃ̂ŁA �ƂȂ�̂ł����A���̎�����A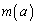 ��a�̎��ŕ\�����Ƃ͂ł��܂���B�A���̔����@�ɂ����
��a�̎��ŕ\�����Ƃ͂ł��܂���B�A���̔����@�ɂ����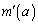 ��a�̎��ŕ\�����Ƃ��ł��܂���B�����ōs���l�܂�܂��B
��a�̎��ŕ\�����Ƃ��ł��܂���B�����ōs���l�܂�܂��B
�����Ō�����ς��āAm��a�̎��ŕ\���̂ł͂Ȃ��Aa��m�̎��ŕ\�����Ƃ��l���Ă݂܂��B �����a�ɂ��ĉ����ƁA
���ӂ̑ΐ����l���āA
�� 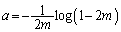 �����m�Ŕ�������ƁA
�����m�Ŕ�������ƁA ��ɕ����Ȃ��`�����Ă���̂ŁA�w�|��̖��̂悤�ɁA���q���o����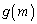 �Ƃ����܂��B
�Ƃ����܂��B 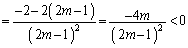 �@(��
�@(�� 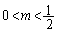 )
)�����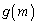 ��m�̌�������
��m�̌�������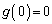 ���A
���A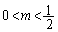 �ɂ�����
�ɂ�����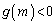
�� 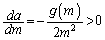 ����āA
����āA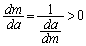 �@(�t���̔����@���Q��)
�@(�t���̔����@���Q��)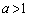 �̂Ƃ��A
�̂Ƃ��A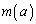 ��a�̑������ŁA
��a�̑������ŁA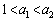 �Ȃ��
�Ȃ��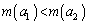 �ƂȂ�܂��B
�ƂȂ�܂��B (3) �@�������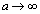 �̂Ƃ��A
�̂Ƃ��A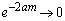 �C
�C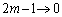 �ƂȂ肻���Ȃ̂ł����A
�ƂȂ肻���Ȃ̂ł����A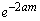 �́A
�́A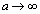 ��
��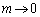 �C
�C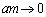 �Ȃ�
�Ȃ�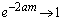 �ɂȂ��Ă��܂������m��܂���B�ł����A
�ɂȂ��Ă��܂������m��܂���B�ł����A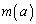 ��a�̑������ł���
��a�̑������ł���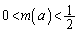 �Ȃ̂ŁA
�Ȃ̂ŁA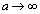 �̂Ƃ�
�̂Ƃ�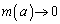 �Ƃ������Ƃ͂��蓾�Ȃ��͂��ł��B�����ŁA
�Ƃ������Ƃ͂��蓾�Ȃ��͂��ł��B�����ŁA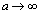 �̂Ƃ�
�̂Ƃ�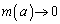 �Ƃ������Ƃ��Ȃ��悤�ɁA
�Ƃ������Ƃ��Ȃ��悤�ɁA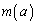 ��a���Œ肵�Ă��܂����Ƃ��l���܂��B
��a���Œ肵�Ă��܂����Ƃ��l���܂��B (2)���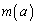 ��a�̑������Ȃ̂ŁA���鐳��
��a�̑������Ȃ̂ŁA���鐳��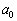 ���Ƃ�ƁA
���Ƃ�ƁA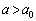 �ƂȂ�a�ɂ���
�ƂȂ�a�ɂ���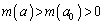
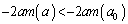
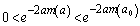
�@���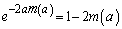
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B