�������嗝�n���w'08�N[3]
e�����R�̐��̒�Ƃ���B���̂Ƃ��A���̊e�₢�ɓ�����B
(1) �ϕ�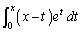 ���v�Z���邱�Ƃɂ��A���̓������ؖ�����B
���v�Z���邱�Ƃɂ��A���̓������ؖ�����B (2) ���ׂĂ̎��R��n�ɂ��āA����
�����藧���Ƃ𐔊w�I�A�[�@�ɂ��ؖ�����B
(3) 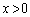 �̂Ƃ��A���ׂĂ̎��R��n�ɂ��āA���̕s���������藧���Ƃ��ؖ�����B
�̂Ƃ��A���ׂĂ̎��R��n�ɂ��āA���̕s���������藧���Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�}�N���[�����W�J���e�[�}�Ƃ������ł��B(2)�́A���w�I�A�[�@���Q�Ƃ��Ă��������B
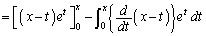 �@(��1����[�@]�ł́Ax��0��t�ɑ�����邱�Ƃɒ��ӁI)
�@(��1����[�@]�ł́Ax��0��t�ɑ�����邱�Ƃɒ��ӁI)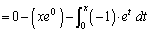
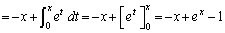
�� 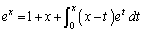 �@(�ؖ��I)
�@(�ؖ��I)
(2) (�T) 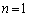 �̂Ƃ��A(1)���A�^�������藧���܂��B
�̂Ƃ��A(1)���A�^�������藧���܂��B (�U) 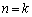 �̂Ƃ��A�^�������藧�Ɖ��肷��ƁA
�̂Ƃ��A�^�������藧�Ɖ��肷��ƁA 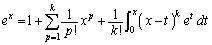 �@����@
�@����@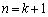 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A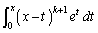 �Ƃ�����ϕ����o�ꂵ�����ł��B���̒�ϕ����A�����ϕ��@�ɂ��v�Z���Ă݂܂��B
�Ƃ�����ϕ����o�ꂵ�����ł��B���̒�ϕ����A�����ϕ��@�ɂ��v�Z���Ă݂܂��B�ƂȂ��āA�@�̉E�ӂɏo�Ă����ϕ�������o���܂��B
������@�ɑ������ƁA
����āA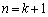 �̂Ƃ����^���͐��藧���܂��B
�̂Ƃ����^���͐��藧���܂��B (�T)�C(�U)���A���ׂĂ̎��R��n�ɂ��āA�^�������藧���܂��B(�ؖ��I)
(3) 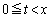 �ɂ����āA
�ɂ����āA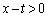 �ł��B������An�����R���Ƃ���Ƃ��A
�ł��B������An�����R���Ƃ���Ƃ��A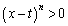 �ł��B�]���āA
�ł��B�]���āA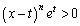 �ƂȂ�܂��B
�ƂȂ�܂��B �� 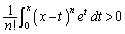 ����āA(2)�̓������A
����āA(2)�̓������A 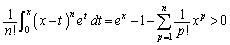 �@����A
�@����A�� 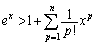 �@(�ؖ��I)
�@(�ؖ��I)
�NjL�D����嗝�n����ɂ��ޑ肪�o�Ă��āA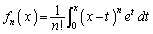 �Ƃ����Ƃ��A
�Ƃ����Ƃ��A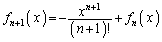 �C
�C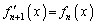 �����藧���Ƃ��������ł��B��L��������A�ł���ł��傤�B�Ȃ��A��L(3)�̇A�ɂ��A
�����藧���Ƃ��������ł��B��L��������A�ł���ł��傤�B�Ȃ��A��L(3)�̇A�ɂ��A �ƂȂ�܂��B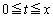 �̂Ƃ�
�̂Ƃ�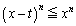 ���A
���A x���Œ肵�āA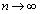 �Ƃ���ƁA�E�Ӂ�0���A
�Ƃ���ƁA�E�Ӂ�0���A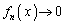
������A �ƂȂ邱�Ƃ�m���Ă���ƁA�s�����̏ؖ�(�����@�̕s�����ւ̉��p(2)���Q��)�Ȃǂł��낢��ȃA�C�f�A���N�����Ƃ�����܂��B
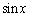 �̃}�N���[�����W�J�́A
�̃}�N���[�����W�J�́A 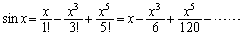 �@(
�@(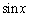 �͊���B
�͊���B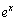 �̊���̍����o���A1�����ƂɁ}�����ւ������̂ɂȂ��Ă���)
�̊���̍����o���A1�����ƂɁ}�����ւ������̂ɂȂ��Ă���)�ƂȂ�܂����A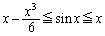 ���ؖ�����悤�Ȗ��(���Ɍ���'08�N)�́A�������痈�Ă��܂��B
���ؖ�����悤�Ȗ��(���Ɍ���'08�N)�́A�������痈�Ă��܂��B
������'95�N���n�ł́A 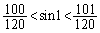 �������B�������A
�������B�������A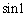 ��1��1���W�A���̈Ӗ��ł���B
��1��1���W�A���̈Ӗ��ł���B�Ƃ�����肪�o�Ă��܂����A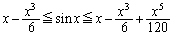 ���ؖ����āA
���ؖ����āA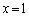 ��������A
��������A �ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B