九州工大情報数学'08年前期[4]
出席者n人の会議で、出席者のうち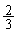 以上が議案に賛成する確率
以上が議案に賛成する確率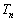 と、
と、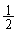 以上が賛成する確率
以上が賛成する確率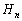 を考える。各出席者が議案に賛成する確率をp (
を考える。各出席者が議案に賛成する確率をp (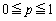 )とし、各出席者が賛成するかしないかは互いに独立であるとする。
)とし、各出席者が賛成するかしないかは互いに独立であるとする。
たとえば、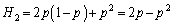 である。
である。
(1) 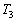 を求めよ。
を求めよ。 (2) 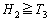 を示せ。
を示せ。 (3) 差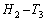 が最も大きくなるときのpの値を求めよ。
が最も大きくなるときのpの値を求めよ。 (4) 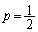 のとき、
のとき、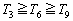 を示せ。
を示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 出席者の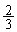 以上が賛成する確率、などと言うと、「憲法改正」の確率でも考えているのかな、と、思ってしまいますが、(1)~(4)はセンター試験の練習程度の問題で、(5)だけ少々技巧を使います。
以上が賛成する確率、などと言うと、「憲法改正」の確率でも考えているのかな、と、思ってしまいますが、(1)~(4)はセンター試験の練習程度の問題で、(5)だけ少々技巧を使います。
(1) 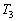 は、出席者3人で
は、出席者3人で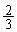 以上が賛成する確率です。2人が賛成するか、3人が賛成するか、です。
以上が賛成する確率です。2人が賛成するか、3人が賛成するか、です。 3人中2人が賛成して1人が反対する場合、反復試行の確率の公式より、その確率は、 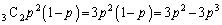 ・・・①
・・・①3人中3人が賛成する確率は、
∴ 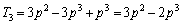 ......[答]
......[答]
(2) 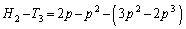
∴ 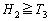
(3) 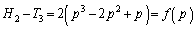
とおくと、
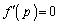 とすると、
とすると、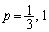
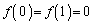 ,
,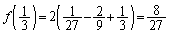
これより増減表は、 増減表より、差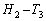 が最も大きくなるとき、
が最も大きくなるとき、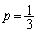 ......[答]
......[答]
(4) 賛成する確率が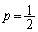 のとき、反対する確率も
のとき、反対する確率も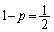 です。
です。 このとき、(1)の結果より、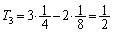
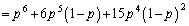 ・・・②
・・・②ですが、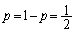 なので、
なので、 同様に、
よって、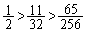 より、
より、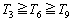
(5) 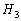 は、出席者3人で
は、出席者3人で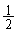 以上が賛成する確率です。2人が賛成するか、3人が賛成するか、なので、
以上が賛成する確率です。2人が賛成するか、3人が賛成するか、なので、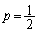 のとき、
のとき、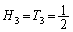
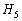 は、出席者5人で、3人が賛成するか、4人が賛成するか、5人が賛成するか、なので、
は、出席者5人で、3人が賛成するか、4人が賛成するか、5人が賛成するか、なので、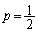 のとき、
のとき、同様に、
とくれば、どうやら、kに無関係に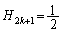 になりそうだ、と、気づきます。
になりそうだ、と、気づきます。
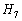 で言えば、
で言えば、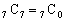 ,
,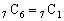 ,
,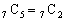 ,
,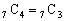 なので、
なので、 になっているんだろう、ということになり、二項定理を利用すればよいことがわかります。
二項定理: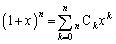
において、n→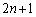 ,x→1とすることにより、
,x→1とすることにより、 ∴ 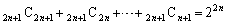 ・・・③
・・・③
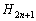 は、出席者
は、出席者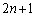 人で
人で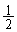 以上が賛成する確率です。n人以上が賛成すればよいので、
以上が賛成する確率です。n人以上が賛成すればよいので、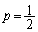 のとき、
のとき、 ③より、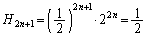 ......[答]
......[答]
追記,(4)で、問題文が、「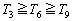 を示せ」となっていて、不等号が等号付きになっているのが気になります。おそらく、最初に作成された問題の案では、
を示せ」となっていて、不等号が等号付きになっているのが気になります。おそらく、最初に作成された問題の案では、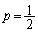 という条件はついていなかったのだろうと思います。
という条件はついていなかったのだろうと思います。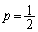 という条件をとってしまうと、
という条件をとってしまうと、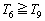 は大変な計算になってしまうので、
は大変な計算になってしまうので、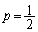 のときだけでよい、ということになったのでしょう。
のときだけでよい、ということになったのでしょう。
ここでは、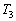 と
と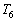 の関係だけでも
の関係だけでも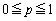 として調べておきます。
として調べておきます。
上記の①,②より、
とおきます。
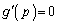 とすると、
とすると、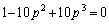 の解がどうなるのか問題になります。
の解がどうなるのか問題になります。
そこで、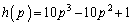 とおいて、
とおいて、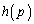 を調べます。
を調べます。
増減表より、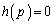 は、
は、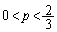 に1解α、
に1解α、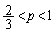 に1解β あることがわかります(関数の増減を参照)。これより
に1解β あることがわかります(関数の増減を参照)。これより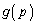 の増減表は以下のようになります。
の増減表は以下のようになります。
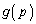 の増減表を見ると、
の増減表を見ると、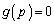 は
は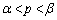 の範囲に解γをもち、
の範囲に解γをもち、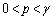 においては、
においては、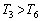 ,
,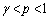 においては、
においては、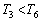 ということがわかります。
ということがわかります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。