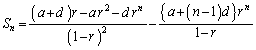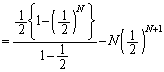����嗝�H���w'08�N���[4]
��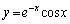 �̃O���t��̓_
�̃O���t��̓_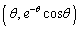 �ɂ�����ڐ���y�ؕЂ�
�ɂ�����ڐ���y�ؕЂ�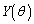 �Ƃ���B���̖₢�ɓ�����B
�Ƃ���B���̖₢�ɓ�����B
(1) 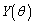 �����߂�B
�����߂�B (2) 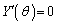 �������̐�θ ������������
�������̐�θ ������������ �Ƃ���B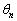 �����߂�B
�����߂�B (3) ��������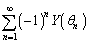 �̘a�����߂�B�������A
�̘a�����߂�B�������A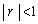 �̂Ƃ�
�̂Ƃ�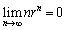 �����藧���Ƃ�p���Ă��悢�B
�����藧���Ƃ�p���Ă��悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ʓ|�Ȍv�Z���ł����A(3)�ɁA(����)�~(����)�̘a�̌`���o�Ă��܂��B���̘a��(����)�̌���ɂ����鐔���������a���A���̘a��������ƁA(����)�̘a�̌`�{�A���t�@�A�ɂȂ��Ęa�����߂���A�Ƃ����̂́A���n���̕K�{�Z�I�ł��B
(1) 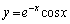
�� 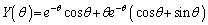 ......[��]
......[��]
(2) 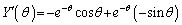
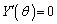 �Ƃ���ƁA
�Ƃ���ƁA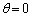 �C
�C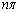 (
(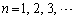 )
)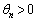 ���A
���A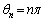 ......[��]
......[��]
(3) 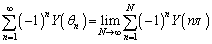
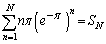 �Ƃ����ƁA
�Ƃ����ƁA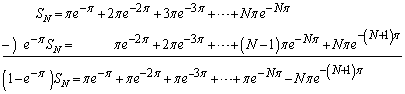
�� 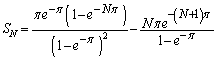 �@����B
�@����B
�A�C�B���@�ɑ������ƁA 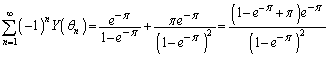 ......[��]
......[��]
�NjL�D��L��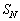 �����߂�Ƃ���́A
�����߂�Ƃ���́A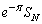 �̍s���A
�̍s���A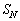 �̍s��1���点�āAe�̎w�������낤�悤�ɏ����A�ォ�牺�������Ƃ��낪�~�\�ł��B
�̍s��1���点�āAe�̎w�������낤�悤�ɏ����A�ォ�牺�������Ƃ��낪�~�\�ł��B
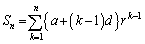 �@����C
�@����C
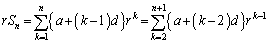 �@����D
�@����D
�� 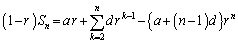
�� 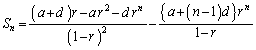
�̂悤�ɕό`�ł���Ƃ悢�Ǝv���܂��B
�{��ł́A�����v�Z�̌��(����)�~(����)�̌`���o�Ă��܂����A���̌`�́A�m���̖��̒��ł悭�o�ꂵ�܂��B
�Ⴆ�A�܂̒��ɔ����ƍ����������Ă��āA���ꂼ��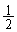 �̊m���Ŏ��o�����s���s���Ƃ��A���������o�������_�Ŏ��s�͏I���A���������o�����ꍇ�ɂ͎��s���J��Ԃ��Ƃ��A���������o���̊��ҒlE�����߂�A�Ƃ����ꍇ�A
�̊m���Ŏ��o�����s���s���Ƃ��A���������o�������_�Ŏ��s�͏I���A���������o�����ꍇ�ɂ͎��s���J��Ԃ��Ƃ��A���������o���̊��ҒlE�����߂�A�Ƃ����ꍇ�A
�E�|�F���A
�� 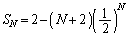
������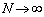 �Ƃ���ƁA
�Ƃ���ƁA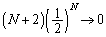
����āA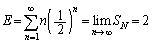
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 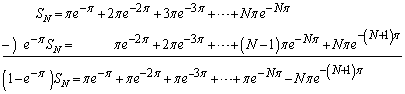
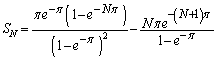 �@����B
�@����B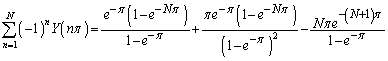
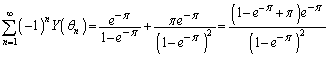 ......[��]
......[��]