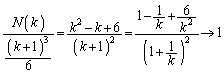�����㐔�w'08�N[4]
���W���ʏ�ɁA����l�F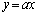 (
(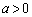 )�ƕ�����C�F
)�ƕ�����C�F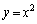 ������Bl��C�Ƃň͂܂ꂽ�̈��D�Ƃ���B�������AD�͋��E���܂ށB�̈�D�Ɋ܂܂�A���Ax�Cy�Ƃ��ɐ����ł���_
������Bl��C�Ƃň͂܂ꂽ�̈��D�Ƃ���B�������AD�͋��E���܂ށB�̈�D�Ɋ܂܂�A���Ax�Cy�Ƃ��ɐ����ł���_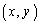 �̌���
�̌���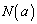 �ŕ\���Ƃ��A���̖₢�ɓ�����B
�ŕ\���Ƃ��A���̖₢�ɓ�����B
(1) �̈�D�̖ʐ�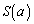 ��a�̎��ŕ\���B
��a�̎��ŕ\���B (3) k�����̐����̂Ƃ��A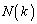 ��k�̎��ŕ\���B
��k�̎��ŕ\���B (4) 1�ȏ�̎���a�ɑ��āA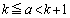 ��������k���Ƃ�Ƃ��A
��������k���Ƃ�Ƃ��A �����藧���Ƃ������B
(5) �O��(1)�ŋ��߂�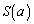 �ɑ��āA
�ɑ��āA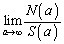 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶����x�Cy���Ƃ��ɐ����ł���_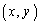 ���A�����ł́u�i�q�_�v�ƌĂԂ��Ƃɂ��܂��B
���A�����ł́u�i�q�_�v�ƌĂԂ��Ƃɂ��܂��B
(1) 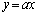 ��
��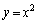 ��A�����āA
��A�����āA
(2)(3) (3)�̈�ʓI�ȏꍇ���l�������邽�߂�(2)������킯�ł����A(2)�����ʼn���Ȃ�A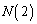 �C
�C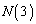 �͐}��`���Ċi�q�_�̐��𐔂��Ă��܂��̂��悢�Ǝv���܂��B
�͐}��`���Ċi�q�_�̐��𐔂��Ă��܂��̂��悢�Ǝv���܂��B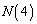 �����܂������悤�Ƃ����
�����܂������悤�Ƃ����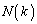 �𐔂���̂Ɠ������Ƃ�����̂ŁA�����ł́A�ꏏ�ɍl���Ă��܂����Ƃɂ��܂��B
�𐔂���̂Ɠ������Ƃ�����̂ŁA�����ł́A�ꏏ�ɍl���Ă��܂����Ƃɂ��܂��B 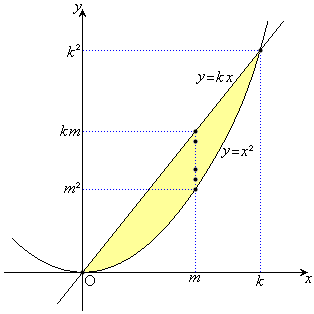
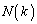 �C�܂�A����
�C�܂�A����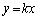 �ƕ�����
�ƕ�����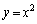 �Ɉ͂܂ꂽ�̈�D��(
�Ɉ͂܂ꂽ�̈�D��(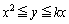 )�̊i�q�_�̐������߂邽�߂ɁAm�𐮐��Ƃ��āA����
)�̊i�q�_�̐������߂邽�߂ɁAm�𐮐��Ƃ��āA����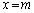 (
(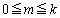 )��̊i�q�_�̐��𐔂��āA
)��̊i�q�_�̐��𐔂��āA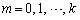 �ɂ��ĉ������킹�邱�Ƃɂ��܂��B
�ɂ��ĉ������킹�邱�Ƃɂ��܂��B
�̈�D�́A����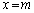 ��ł́A
��ł́A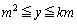 �@����@ �̕����ɑ��݂���̂ŁA����
�@����@ �̕����ɑ��݂���̂ŁA����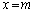 ��ɑ��݂���i�q�_�̐��́A�@���݂�������y�̌��ɂȂ�܂��B
��ɑ��݂���i�q�_�̐��́A�@���݂�������y�̌��ɂȂ�܂��B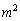 ��
��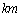 �������Ȃ̂ŁA���̌��́A
�������Ȃ̂ŁA���̌��́A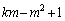 �ł�(
�ł�(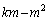 �ł͂���܂���I3����7�܂Ő�����
�ł͂���܂���I3����7�܂Ő�����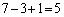 ����܂�)�B����āA
����܂�)�B����āA����āA(2)�́A
(3)�́A
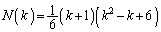 ......[��]
......[��]
(4) k�𐳂̐����Ƃ��āA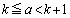 �̂Ƃ��A
�̂Ƃ��A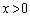 �ł���A
�ł���A 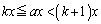 �@����A
�@����A�̈�D��a�̒l�ɂ���ĕς��̂ŁA
�Ə������Ƃɂ���ƁA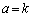 �̂Ƃ��̗̈�D��
�̂Ƃ��̗̈�D��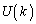 �C
�C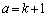 �̂Ƃ��̗̈�D��
�̂Ƃ��̗̈�D��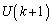 �ł��B
�ł��B
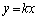 �C
�C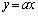 �C
�C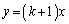 �̂��ꂼ���
�̂��ꂼ���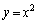 �Ƃ̌�_�́Ak�Ca�C
�Ƃ̌�_�́Ak�Ca�C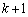 �ł����A
�ł����A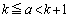 �Ȃ̂ŁA�A�ƍ��킹�āA
�Ȃ̂ŁA�A�ƍ��킹�āA 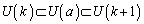 �@����B�@(�W�����Q��)
�@����B�@(�W�����Q��)�ł��B���m�Ɍ����ƁA�B�̍����̕�܊W�̋L���e��'��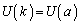 �̏ꍇ�����蓾�܂����A�E���́e��'�ł�
�̏ꍇ�����蓾�܂����A�E���́e��'�ł�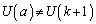 �ł��B
�ł��B
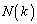 �C
�C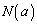 �́A
�́A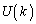 �C
�C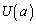 ���̊i�q�_�̌��Ȃ̂ŁA�B�̍����̕�܊W����A
���̊i�q�_�̌��Ȃ̂ŁA�B�̍����̕�܊W����A 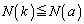 �@����C
�@����C�ł��B
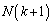 ��
��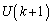 ���̊i�q�_�̌��Ȃ̂ŁA�B�̉E���̕�܊W����
���̊i�q�_�̌��Ȃ̂ŁA�B�̉E���̕�܊W���� �Ƃ����s�������ł��܂�((5)�͂��̕s������p���ē����邱�Ƃ��ł��܂�)���A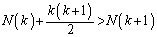 �������Ȃ��̂ŁA�^�s�������������Ƃ��ł��܂���B
�������Ȃ��̂ŁA�^�s�������������Ƃ��ł��܂���B
��L�̂悤�ɁA�B�̉E���̕�܊W�ł�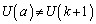 �Ȃ̂ł����A�A���A����
�Ȃ̂ł����A�A���A����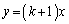 ���
���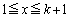 �̕����̊i�q�_�́A
�̕����̊i�q�_�́A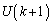 �ɂ͊܂܂�܂���
�ɂ͊܂܂�܂���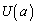 �ɂ͊܂܂�܂���B���̊i�q�_�̐���
�ɂ͊܂܂�܂���B���̊i�q�_�̐���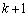 �ł��B����āA
�ł��B����āA 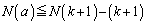 �@����D
�@����D�ł��B���̉E�ӂ�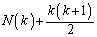 ���r���܂��B
���r���܂��B �� 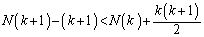 �D���A
�D���A 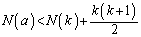 �@����E
�@����E�C�C�E���A
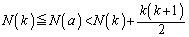 �@����F
�@����F����Ŏ����܂����B
(5) (4)�Ŏ������s�����F�̊e�ӂ�f����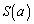 �Ŋ���̂ł́Aa�Ck��2�������o�Ă��āA�͂��݂����Ɏ������݂ɂ����̂ŁA������1�ɂ���悤�ɍH�v���܂��B
�Ŋ���̂ł́Aa�Ck��2�������o�Ă��āA�͂��݂����Ɏ������݂ɂ����̂ŁA������1�ɂ���悤�ɍH�v���܂��B 1�ȏ�̎���a�ɑ��āA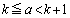 ��������k���Ƃ�Ƃ��A
��������k���Ƃ�Ƃ��A ����ƇF���A
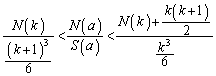 �@����G
�@����G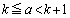 ���A
���A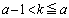 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA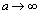 �̂Ƃ�
�̂Ƃ�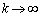 �ł��B
�ł��B
�G�̍��ӂɂ��āA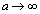 �C�]����
�C�]����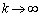 �̂Ƃ��A
�̂Ƃ��A�G�̉E�ӂɂ��āA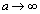 �C�]����
�C�]����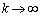 �̂Ƃ��A
�̂Ƃ��A 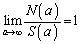 ......[��]
......[��]
�NjL�D�悭����i�q�_�̐��𐔂�����ŁA�i�q�_�̐��Ɩʐς��Ɍ��ɂ����Ĉ�v����A�Ƃ������_���o�Ă���̂ł����A���́A���̉F���̊�{�����͂��������Ƃ���ɂ��邾�낤�Ǝv���Ă��܂��B
���̖��ł́A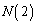 �C
�C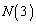 �C
�C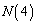 ���炢�̂����́A���ꂢ�ȊW�ŕ���ł���Ƃ͌����Ȃ��̂ł����A
���炢�̂����́A���ꂢ�ȊW�ŕ���ł���Ƃ͌����Ȃ��̂ł����A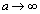 �̋Ɍ����l�����
�̋Ɍ����l�����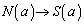 �ƂȂ�A���ϕ��w�̌��ʂƈ�v����悤�ɂȂ�̂ł��B
�ƂȂ�A���ϕ��w�̌��ʂƈ�v����悤�ɂȂ�̂ł��B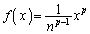 (n�Cp�͐�����)�Ƃ��āA
(n�Cp�͐�����)�Ƃ��āA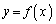 (�_
(�_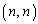 ��ʂ�܂�)��x���A����
��ʂ�܂�)��x���A����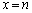 �ň͂܂��̈�
�ň͂܂��̈�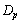 ���̊i�q�_�̐�
���̊i�q�_�̐�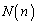 ���l���܂��B
���l���܂��B
�����̖��Ɠ����悤�ɂ��āAm��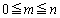 ���݂����������Ƃ��A����
���݂����������Ƃ��A����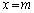 ��̊i�q�_(
��̊i�q�_(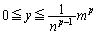 �͈̔͂ɂ���)�̐��𐔂���ƁA
�͈̔͂ɂ���)�̐��𐔂���ƁA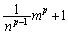 ����܂��B
����܂��B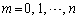 �ɂ��ĉ������킹��ƁA
�ɂ��ĉ������킹��ƁA 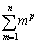 �ł����A
�ł����A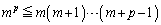 �𗘗p���āA
�𗘗p���āA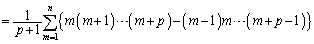
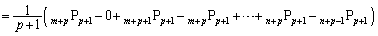 �@(�A��
�@(�A��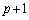 �̐����̐ς�����L����p���ĕ\���܂����B�r�����ł����������ď����܂�)
�̐����̐ς�����L����p���ĕ\���܂����B�r�����ł����������ď����܂�)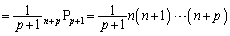
�� 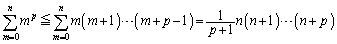 ���l��
���l��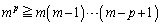 �𗘗p���āA
�𗘗p���āA �����ŁA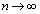 �Ƃ���ƁA���ӂ��E�ӂ�
�Ƃ���ƁA���ӂ��E�ӂ�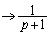 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA �ƂȂ�܂��B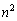 ��
��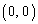 �C
�C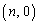 �C
�C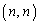 �C
�C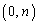 ��4���_�Ƃ��鐳���`�̖ʐςł����A�̈�
��4���_�Ƃ��鐳���`�̖ʐςł����A�̈�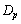 �̖ʐς́A
�̖ʐς́A �ƂȂ�̂ŁA�i�q�_�̐�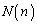 �́A
�́A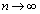 �̋Ɍ��ŁA��ϕ��ɂ�蓾����̈�
�̋Ɍ��ŁA��ϕ��ɂ�蓾����̈�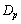 �̖ʐ�S�ɋ߂Â��̂ł��B
�̖ʐ�S�ɋ߂Â��̂ł��B
�܂�A���ϕ��w�́A�i�q�_�������ɑ����Ƃ��̌��ʂƈ�v����A�Ƃ������Ƃł��B
�����w�̊�{�@���͔��ϕ��ŕ\����܂����A�i�q��ɕ���{���q�̐U�镑�����ɐ������̗��q�ɂ��ĊW�߂�ƁA�^�����������d���U���̖@���ɂȂ�̂��낤�A�ƁA���͎v���܂��B����䂦�A�����w�̑Ώۂ������ׂȕ����ɐi�߂Ă����ƁA���d���ʂ�v�����N�̗ʎq�����A�{�[�A�̌��q�͌^�̂悤�ȁA1�A2�A����A�Ɛ����Ă����i�q�_�I�Ȍ��ʂ������Ă���̂ł��B2008�N10���ɁA�N�H�[�N�̌������s�������ѐ����m�A�v��q�p���m�ƂƂ��ɁA�암�z��Y���m���A�J�C�����Ώ̐��̎����I�j��ɂ��N�H�[�N�̎��ʊl���̗��_�̐��ʂɂ��m�[�x�������w�܂���܂��܂����B2007�N�ɋ��s��w�̌����`�[�����ʎq�i�q�̗��_���g���ăR���s���[�^�E�V�~�����[�V�������s���A�암���m�̗��_�̌��ɐ������Ă��邻���ł��B�ڂ������_�̒��g��m��܂��A���������������A���̒����w�̖��̉�����ɂ���̂����m��܂���B
���̑����́A���̃E�F�u�T�C�g�������̓ǎҏ����ɂ��Ѝl���Ē��������Ǝv���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 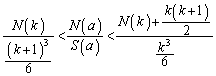 �@����G
�@����G