���l�s��㐔�w'08�N[4]
4��������
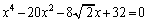 �@���(��)
�@���(��)
(1) ������(��)�͋�� �ɉ��������Ƃ������B
�ɉ��������Ƃ������B (2) (1)�ʼn����I�C���[(Leonhard Euler)�̕��@�ŋ��߂悤�Bp�Cq�Cr�𐳂̎����Ƃ���
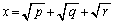 �@(
�@( )
)�Ƃ����B�܂��A�⏕�ϐ�f�Cg�Ch
������B �C
�C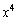 ���v�Z���āA4��������
���v�Z���āA4�������� 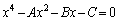 �@���(����)
�@���(����)�Ƃ����Ƃ�A�CB�CC��f�Cg�Ch��p���ĕ\���B����(��)��(����)���������Ɖ��肵��f�Cg�Ch�����߂�B
(3) ����
��(2)�œ���ꂽf�Cg�Ch��p����3��������
��3�̉�p�Cq�Cr�����߂�B
(4) ������(��)�̉�
��
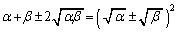 �@(
�@(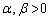 )
)��p���Ċȗ������A���ꂪ���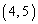 �ɂ��邱�Ƃ������B
�ɂ��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������Ƃ��Ă͌v�Z���邾���ł����A4���������̈�ʓI��@���l�^�Ƃ��������[���e�[�}�̖��ł��B�Ȃ��������������Q�Ƃ��Ă��������B
�܂��A��蕶���̋�� �́A
�́A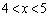 �͈̔́A�Ƃ����Ӗ��ł��B
�͈̔́A�Ƃ����Ӗ��ł��B
(1) 
�Ƃ����܂��B
����āA������(��)�͋�� �ɉ��������܂��B
�ɉ��������܂��B
(2) 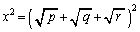
�����ŁA �Ƃ����ƁA��蕶����f��p���āA
�Ƃ����ƁA��蕶����f��p���āA 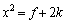 �@����@
�@����@
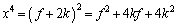 �@����A
�@����A���̒���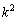 �́A��蕶����g�Ch��p���āA
�́A��蕶����g�Ch��p���āA �@���A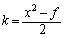
�A���A �� 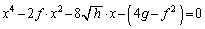
(����)�Ɣ�r����ƁA (��)��(����)���r����ƁA
(3) 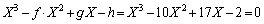
�萔���� �̖�
�̖�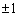 �C
�C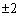 �������Ă����ƁA
�������Ă����ƁA ���������Ƃ��ɁA
���������Ƃ��ɁA 3�̉�p�Cq�Cr�́A2�C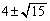 ......[��]
......[��]
(4) 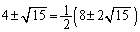 �́A��蕶���̓����ɂ��Ă͂߂�ƁA
�́A��蕶���̓����ɂ��Ă͂߂�ƁA 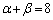 �C
�C
������݂���α�Cβ�́A3��5
������A
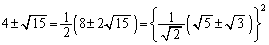 �@(��������)
�@(��������)����āA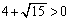 �C
�C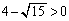 ���l�����āA
���l�����āA ���A
�ƂȂ�܂��B
�NjL�D�{��ɍ��킹���̂��A3�����������������Ƃ��������o�Ă��܂��B
��s��'08�N���[1]�F
�ȉ��̖₢�ɓ�����B
(1) ���ׂĂ̎���x�Cy�Cz�ɑ��Ď��̓��������藧�悤�Ȏ����̑g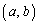 ��1�g���߂�B
��1�g���߂�B �������Ai�͋����P�ʂƂ���B
(2) 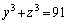 �C
�C ���������̑g
���������̑g ��1�g���߂�B
��1�g���߂�B (3) 3��������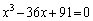 �̉������ׂċ��߂�B
�̉������ׂċ��߂�B
���@(1) ���������̌����F
���L�����Ă���A������g���悢�̂ł����A�L�����Ă��Ȃ���A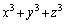 ���o�Ă���悤�ɁA
���o�Ă���悤�ɁA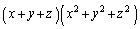 ���l���܂��B
���l���܂��B �� 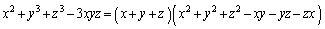
���J�b�R���ɂ��āA
�܂�A (��������)�Ƃ������Ƃ́A
(��������)�Ƃ������Ƃ́A ����āA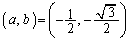 ......[��]
......[��]
(2) 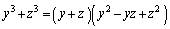
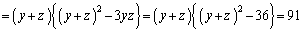 �@����@
�@����@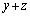 �C
�C �͐����Ȃ̂ŁA
�͐����Ȃ̂ŁA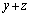 ��91�̖ł��B
��91�̖ł��B
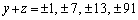 �̒�����@���݂������̂�T���ƁA
�̒�����@���݂������̂�T���ƁA ���Ay�Cz�́A
���Ay�Cz�́A��2���ŁA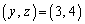 ......[��]
......[��]
(3) (1)�ɂ����āA �C
�C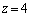 �Ƃ���ƁA
�Ƃ���ƁA ���A
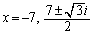 ......[��]
......[��]
3���������̈�ʓI��@�ɂ��ẮA�J���_�m�̉�@���m���Ă��āA'94�N���{��ȑ�[1]�ŏo�肳��Ă��܂��B3���������A4���������̈�ʉ��ɋ����������ꂽ���́A�u�㐔�w�u�`�E�����V�Łv���ؒ厡��(�����o��)�̑�6�͂��Q�l�ɂ��Ă��������B���́A���̖{�ƍ��ؒ厡����́u���������_�u�`�v�͓������̃l�^�Ƃ��Ă悭�g���Ă��āA���Ԃɗ]�T�̂�����͈�ǂ̉��l������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B