�R�`��H���w'08�N[4]
���� ��
��
 �@(
�@(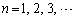 )
)
(1)  �C
�C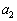 �����߂�B
�����߂�B (2) �����ϕ��@��p���āA �������B
�������B (3)  �Ƃ����Ƃ��A
�Ƃ����Ƃ��A �������B
�������B (4) 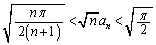 �������A
�������A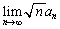 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@ �Ȃ̂ŁA
�Ȃ̂ŁA �ł���A���̖���
�ł���A���̖���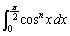 �ɂ��Č����邱�Ƃ�
�ɂ��Č����邱�Ƃ� �ɂ��Ă������܂��B
�ɂ��Ă������܂��B
(4)�́A�����Y�ނ����m��܂���B�����ł́A�Y�ނƂ��납�����Ă݂܂��B
�Ȃ��A��ϕ��̑Q�������Q�Ƃ��Ă��������B
(3) �@�𗘗p���邽�߂ɁA �̓Y����1���炵�āA
�̓Y����1���炵�āA �Ƃ��Ă݂܂��B
�Ƃ��Ă݂܂��B �@�������āA
�� 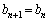 ����āA
����āA  �@(�� (1))
�@(�� (1))
(4) (3)���A
 �@����A
�@����A �ɂ����āA
�ɂ����āA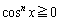 (������
(������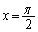 �̂Ƃ�����)�Ȃ̂ŁA
�̂Ƃ�����)�Ȃ̂ŁA �ł��B�Ƃ������Ƃ́A
�ł��B�Ƃ������Ƃ́A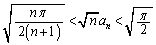 ��
�� 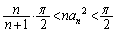 �@���(��)
�@���(��)�ł��B�����ŁA(��)���������Ƃɂ��܂��B(��)�̍����̕s�����́A�A�̗��ӂ� �������āA
�������āA �Ƃ��āA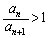 �ł�����A
�ł�����A �Ƃ��ē��������ł��B(��)�̉E���̕s�����́A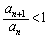 �ł�����A�A�̍��ӂ�
�ł�����A�A�̍��ӂ�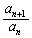 �����������̂�
�����������̂� ���r���邱�Ƃɂ��A
���r���邱�Ƃɂ��A �Ƃ��āA
���瓱�������ł��B
�Ƃ������Ƃ́A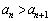 ���������(��)�������邱�ƂɂȂ�܂��B
���������(��)�������邱�ƂɂȂ�܂��B
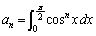 �C
�C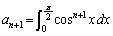 �Ȃ̂ŁA
�Ȃ̂ŁA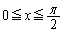 �ɂ����āA
�ɂ����āA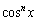 ��
��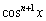 ���ׂ邱�ƂɂȂ�܂��B���Ă͈ȉ��̂悤�ɂȂ�ł��傤�B
���ׂ邱�ƂɂȂ�܂��B���Ă͈ȉ��̂悤�ɂȂ�ł��傤�B
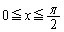 �ɂ����āA
�ɂ����āA (������
(������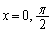 �̂Ƃ�����)���A
�̂Ƃ�����)���A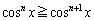
����āA �܂��A �ɂ����āA
�ɂ����āA (������
(������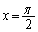 �̂Ƃ�����)���A
�̂Ƃ�����)���A (3)���A
 �@����A
�@����A�A�̗��ӂɁA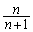 �������āA
�������āA �� 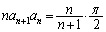
 ���A
���A �� 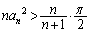 �@����B
�@����B
�A��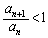 �Ƃ���A
�Ƃ���A �� 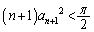
 �Ȃ̂ŁA
�Ȃ̂ŁA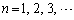 �ɑ��āA
�ɑ��āA
�� 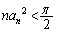 �@����C
�@����C
�B�C�C���A  ���A
���A��  ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B