�k�嗝�n���w'09�N���[4]
��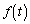 ��
��
�ƒ�߂�B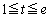 �ł�
�ł�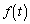 �̍ŏ��l�Ƃ��̂Ƃ���t�̒l�����߂�B
�̍ŏ��l�Ƃ��̂Ƃ���t�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��Βl���܂ޒ�ϕ��̍ő�E�ŏ��̖��ł����A��ϕ����̒��ɐ�Βl��2�o�Ă��܂��B2�̐�Βl�̒���0�ɂ���t�̒l�͈قȂ�̂ŁA�ʁX�ɐ�Βl���O���Ȃ�������܂���B
�Ƃ��āA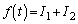 �ł��B
�ł��B
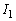 �ɂ��ẮA��Βl�L���̓�����0�ɂ���ƁA
�ɂ��ẮA��Βl�L���̓�����0�ɂ���ƁA
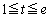 �ł�
�ł�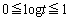 �Ȃ̂ŁA��ϕ��̐ϕ���Ԃ��A
�Ȃ̂ŁA��ϕ��̐ϕ���Ԃ��A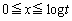 �C
�C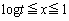 �Ƃ���2��Ԃɕ����܂��B
�Ƃ���2��Ԃɕ����܂��B
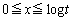 �ɂ����Ă�
�ɂ����Ă�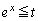 �C
�C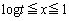 �ɂ����Ă�
�ɂ����Ă�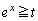
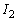 �ɂ��ẮA��Βl�L���̓�����0�ɂ���ƁA
�ɂ��ẮA��Βl�L���̓�����0�ɂ���ƁA
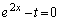 ��
�� 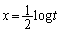
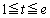 �ł�
�ł�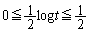 �Ȃ̂ŁA��ϕ��̐ϕ���Ԃ��A
�Ȃ̂ŁA��ϕ��̐ϕ���Ԃ��A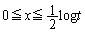 �C
�C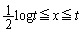 �Ƃ���2��Ԃɕ����܂��B
�Ƃ���2��Ԃɕ����܂��B
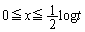 �ɂ����Ă�
�ɂ����Ă�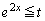 �C
�C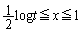 �ɂ����Ă�
�ɂ����Ă�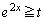
�@�C�A���A
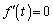 �Ƃ���ƁA
�Ƃ���ƁA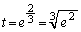 �@(
�@(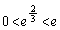 �ł�)
�ł�)
�����\(���̑������Q��)���A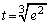 ......[��] �̂Ƃ��A�ŏ��l�F
......[��] �̂Ƃ��A�ŏ��l�F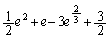 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B