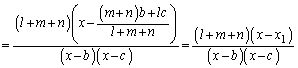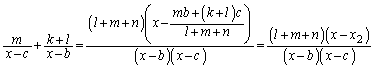�_�ˑ嗝�n���w'09�N���[5]
a�Cb�Cc�Cd������(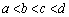 )�Ƃ��Ak�Cl�Cm�Cn�����R���Ƃ���B����x�̊�
)�Ƃ��Ak�Cl�Cm�Cn�����R���Ƃ���B����x�̊�
�ɂ��āA�ȉ��̂��Ƃ������B
(1) a�Cb�Cc�Cd�ƈقȂ�x�ɑ��āA
�����藧�B
(2) 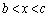 �͈̔͂�x�ɑ��āA
�͈̔͂�x�ɑ��āA �����藧�B
(3) ����2�̏������ɖ���������t�����݂���B
(i) 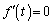
(ii) 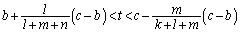
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�́A(2)�Ƃ̊֘A���C�Â��ɂ����̂ł����A�C�Â��Ă��܂��A(2)�̕s�����̍��ӂƉE�ӂ̓����ׂ邱�Ƃɂ��������܂��B
(1) 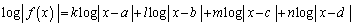
(2) 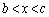 �͈͓̔���x�ɑ��āA
�͈͓̔���x�ɑ��āA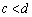 �C
�C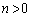 ���A
���A ���ӂ�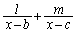 �������āA
�������āA (1)�̌��ʂ�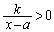 ���A
���A �� 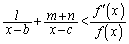 �@����@
�@����@
���l�ɁA �͈͓̔���x�ɑ��A
�͈͓̔���x�ɑ��A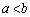 �C
�C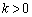 ���A
���A ���ӂ�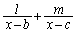 �������āA
�������āA (1)�̌��ʂ� ���A
���A  �@����A
�@����A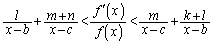
(3) ��蕶��(i)��(ii)�Ō����Ă��邱�Ƃ́A������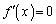 �̉�t���A
�̉�t���A �͈̔͂ɂ���A�Ƃ������Ƃł��B���͈̔͂̍��[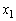 �ƉE�[
�ƉE�[ �́A
�́A 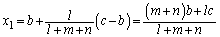 �C
�C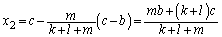
������A���[�́A��������� ��
��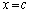 ���Al�F
���Al�F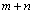 �ɓ�������Ƃ���ɂ���A�E�[�́A
�ɓ�������Ƃ���ɂ���A�E�[�́A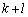 �Fm�ɓ�������Ƃ���ɂ���܂��B�����(2)�����p�ł��������A�Ƃ������Ƃ��킩��܂��B(2)�̕s�����̍��ӂ́A
�Fm�ɓ�������Ƃ���ɂ���܂��B�����(2)�����p�ł��������A�Ƃ������Ƃ��킩��܂��B(2)�̕s�����̍��ӂ́A (2)�̕s�����̉E�ӂ́A
�ƕό`�ł��܂��B�܂�A������ �̉�t�́A(2)�̕s�����̍��ӂƉE�ӂ��[���ɂ���l�̊Ԃɂ���킯�ł��B�����ŁA(2)�̕s�����̍��ӂƉE�ӂ�
�̉�t�́A(2)�̕s�����̍��ӂƉE�ӂ��[���ɂ���l�̊Ԃɂ���킯�ł��B�����ŁA(2)�̕s�����̍��ӂƉE�ӂ� �C
�C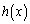 �Ƃ����āA�ǂ�ȕω������邩�ׂĂ݂܂��B
�Ƃ����āA�ǂ�ȕω������邩�ׂĂ݂܂��B ���A �ɂ����āA
�ɂ����āA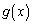 ���P�������ŁA
���P�������ŁA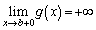 �C
�C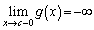 �C������
�C������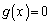 �́A���͈̔͂ɂ���1�̎�����
�́A���͈̔͂ɂ���1�̎�����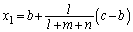 �������܂��B
�������܂��B ���A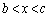 �ɂ����āA
�ɂ����āA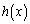 �͒P�������ŁA
�͒P�������ŁA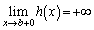 �C
�C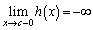 �C������
�C������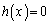 �́A���͈̔͂ɂ���1�̎�����
�́A���͈̔͂ɂ���1�̎�����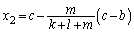 �������܂��B(2)���A
�������܂��B(2)���A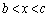 �͈̔͂�x�ɑ��āA
�͈̔͂�x�ɑ��āA 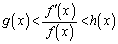 �@����B
�@����B�܂��A �̂Ƃ��A
�̂Ƃ��A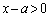 �C
�C �C
�C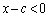 �C
�C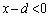 �C�]���āA
�C�]���āA �C
�C �C
�C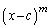 �C
�C �͒蕄���Ȃ̂ŁA
�͒蕄���Ȃ̂ŁA ���蕄����
���蕄����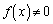 �ł��B
�ł��B
����āA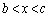 �ɂ����āA�B���A
�ɂ����āA�B���A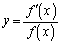 �̃O���t�́A
�̃O���t�́A �̃O���t������A
�̃O���t������A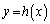 �̃O���t��������ʂ�̂ŁA
�̃O���t��������ʂ�̂ŁA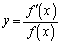 �̘A�������A����(i)�C(ii)��������t�����݂��܂��B
�̘A�������A����(i)�C(ii)��������t�����݂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B