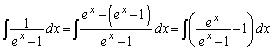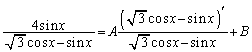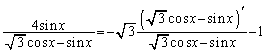�F�{�嗝�n���w'09�N[4]
���̖₢�ɓ�����B
(��1)�@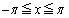 �̂Ƃ��A
�̂Ƃ��A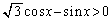 ���݂���x�͈̔͂����߂�B
���݂���x�͈̔͂����߂�B (��2)�@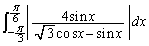 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��2�ł́A��ϕ����ɐ�Βl�L�������Ă��܂����A��1�ł��̕���̕����ׂ�悤�ɂȂ��Ă��܂��B�ϕ��́A�u���ϕ��Ȃǂ��Ȃ��Ȃ����܂��s���Ȃ��̂ŁA���X�Y�ނ����m��܂���B
δ �́A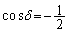 �C
�C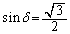 �����p�ŁA�Ⴆ�A
�����p�ŁA�Ⴆ�A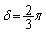
����āA
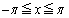 �̂Ƃ��A
�̂Ƃ��A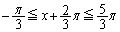
���͈̔͂�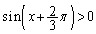 �ƂȂ�̂́A
�ƂȂ�̂́A �C�܂�A
�C�܂�A �̂Ƃ��B
�̂Ƃ��B
���߂�x�͈̔͂́A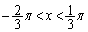 ......[��]
......[��]
(��2)�@(��1)�̌��ʂ��A�ϕ���� �ɂ����āA
�ɂ����āA
 �ɂ�����
�ɂ�����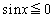 �C
�C �ɂ�����
�ɂ�����
����āA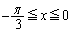 �ɂ����āA
�ɂ����āA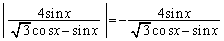
 �ɂ����āA
�ɂ����āA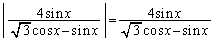
�ȏ���A�����ŁA���X����܂��B �͂��̌`�̂܂܂ł́A���n�������߂��܂���B����ƂāA
�͂��̌`�̂܂܂ł́A���n�������߂��܂���B����ƂāA �ȂǂƂ����Ă��A�ϕ��ł���`�������Ă��܂���B�܂��A�����ϕ������܂��s���`�ł�����܂���B
�ȂǂƂ����Ă��A�ϕ��ł���`�������Ă��܂���B�܂��A�����ϕ������܂��s���`�ł�����܂���B
���������Ƃ��ɁA�g�����i�ɁA�����F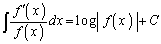 (�s��ϕ��̌������Q��)�̗��p������܂��B
(�s��ϕ��̌������Q��)�̗��p������܂��B
�ł����A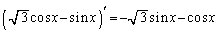 �ł����āA
�ł����āA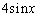 �ɂȂ�܂���B
�ɂȂ�܂���B
���̌����́A���̂܂ܓK�p�ł��Ȃ��Ă��A�����ό`����Ǝg���邱�Ƃ�����܂��B �̂悤�ɁA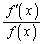 �ƒ萔�̘a�⍷�̌`�ɕό`����ΐϕ��ł���킯�ł��B
�ƒ萔�̘a�⍷�̌`�ɕό`����ΐϕ��ł���킯�ł��B
�@�ł��A���̕ό`���ł��Ȃ����A �Ƃ����Ē��ׂĂ݂�ƁA
 �C
�C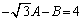
�A�����ĉ����ƁA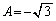 �C
�C
�܂�A ������A
 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)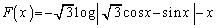 �Ƃ����ƁA�@�́A
�Ƃ����ƁA�@�́A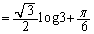 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B