�����㐔�w'09�N[4]
���ׂĂ̐��̎���x�ɑ��Ē�`���ꂽ�A����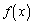 �͎���(a)�C(b)�������̂Ƃ���B
�͎���(a)�C(b)�������̂Ƃ���B
(a) ���ׂĂ̐��̎���x�Cy�ɑ���
(b) ���ׂĂ̎��R��n�ɑ���
���̊� �ɂ��āA���̖₢�ɓ�����B
�ɂ��āA���̖₢�ɓ�����B
(1) x�𐳂̎����Ƃ���Ƃ��A���̒l�����߂�B
(2) a��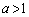 �����L�����Ƃ���Ƃ��A���̕s�������ؖ�����B
�����L�����Ƃ���Ƃ��A���̕s�������ؖ�����B (3) a�Cb��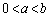 �����L�����Ƃ���Ƃ��A���̕s�������ؖ�����B
�����L�����Ƃ���Ƃ��A���̕s�������ؖ�����B (4) a�Cb��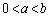 ���������ł�(3)�̕s���������藧���Ƃ�p���āA���̎���x�Cy�ɑ��āA���̕s�������ؖ�����B
���������ł�(3)�̕s���������藧���Ƃ�p���āA���̎���x�Cy�ɑ��āA���̕s�������ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶�̊�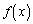 �́A����(a)�C(b)����A�ΐ���
�́A����(a)�C(b)����A�ΐ���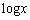 �̂悤�Ȋ���z�肵�čl���܂��B(1)�Ȃ�A
�̂悤�Ȋ���z�肵�čl���܂��B(1)�Ȃ�A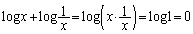 ���낤�Ƃ������ƂɂȂ�܂��B
���낤�Ƃ������ƂɂȂ�܂��B
(4)�̕s�����́A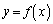 �̃O���t����ɓ��ȋȐ��ł��邱�Ƃ��Ӗ����Ă��܂��B���̌`�̂܂܋��s�����ɁA(3)�𗘗p����A�Ƃ�����蕶�̎w��ɏ]���āA�ό`���Ă��玦���悤�ɂ��܂�(�s�����̏ؖ����Q��)�B
�̃O���t����ɓ��ȋȐ��ł��邱�Ƃ��Ӗ����Ă��܂��B���̌`�̂܂܋��s�����ɁA(3)�𗘗p����A�Ƃ�����蕶�̎w��ɏ]���āA�ό`���Ă��玦���悤�ɂ��܂�(�s�����̏ؖ����Q��)�B
(1) (a)�ɂ����āA �Ƃ���ƁA
�Ƃ���ƁA �܂��A(a)�ɂ����āA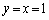 �Ƃ���ƁA
�Ƃ���ƁA �� 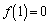 �@����@
�@����@
�� 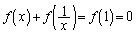 ......[��]
......[��]
(2) a��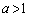 �����L�����̂Ƃ��A
�����L�����̂Ƃ��A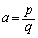 �C
�C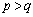 �ƂȂ鎩�R��p�Cq�����݂��܂��B
�ƂȂ鎩�R��p�Cq�����݂��܂��B (1)�̌��ʂɂ����āA �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A �� 
(b)���J��Ԃ��p���邱�Ƃɂ��A
��  �@(�ؖ��I)
�@(�ؖ��I)
(3) 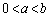 ���A
���A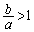
(2)�̌��ʂ��A�L���� �ɂ��āA
�ɂ��āA (1)�̌��ʂ��A
�� 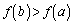 �@(�ؖ��I)
�@(�ؖ��I)
(4) (3)���g����`�ɕό`���܂��B
�ƂȂ�̂ŁA
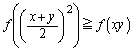 �@����A
�@����A�� 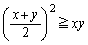 �@(������
�@(������ �̂Ƃ��ɐ���)
�̂Ƃ��ɐ���) �E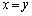 �̂Ƃ��A
�̂Ƃ��A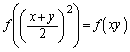 �ƂȂ�A�̓������������܂��B
�ƂȂ�A�̓������������܂��B �E �̂Ƃ��A
�̂Ƃ��A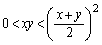 ���A(3)�̌��ʂɂ����āA
���A(3)�̌��ʂɂ����āA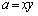 �C
�C �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A �ȏ���A�A���������A
 �@(�ؖ��I)
�@(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 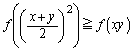 �@(�� (1))
�@(�� (1))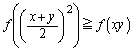 �@����A
�@����A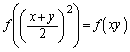 �ƂȂ�A�̓������������܂��B
�ƂȂ�A�̓������������܂��B