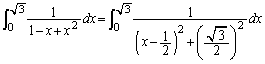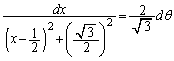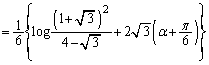�啪��㐔�w'09�N[1]
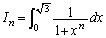 (
(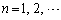 )
)
�Ƃ����Ƃ��A���̖₢�ɓ�����B
(1) 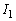 �C
�C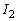 �̒l�����߂�B
�̒l�����߂�B (2) 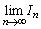 �̒l�����߂�B
�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ϕ����̒���n���o�Ă���̂ŁA��ϕ��̑Q�������l�������Ȃ�܂����A(1)������A�����ƕʂ̂��Ƃ��l���Ȃ�������܂���B
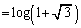 ......[��]
......[��] ......[��]
......[��]
(2) (1)��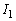 �C
�C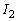 �̌��ʂ�����A
�̌��ʂ�����A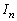 �𐔗�̈�ʍ��ƌ��đQ�������l����̂ł͓W�]���Ȃ����Ƃ͖��炩�ł��B���ƌ�����
�𐔗�̈�ʍ��ƌ��đQ�������l����̂ł͓W�]���Ȃ����Ƃ͖��炩�ł��B���ƌ�����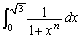 �̌v�Z���W�]������܂���B
�̌v�Z���W�]������܂���B ��ϕ����̒��ɏo�Ă���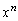 �́A
�́A �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A �ƂȂ�܂����A
�ƂȂ�܂����A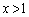 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�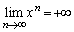 �ƂȂ�̂�
�ƂȂ�̂� �ł���A
�ł���A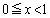 ��
��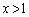 �Ƃ��čl����K�v�����邱�Ƃ��킩��܂��B�����ŁA�ϕ���Ԃ�
�Ƃ��čl����K�v�����邱�Ƃ��킩��܂��B�����ŁA�ϕ���Ԃ� �C
�C �ɕ������āA
�ɕ������āA �Ƃ��čl���邱�Ƃɂ��܂��B
�܂��A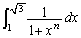 �ł����A
�ł����A �ɂ�����
�ɂ�����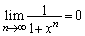 �Ȃ̂ŁA
�Ȃ̂ŁA �ƂȂ肻���ł��B�����ŁA
�ƂȂ肻���ł��B�����ŁA �C
�C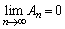 �ƂȂ�
�ƂȂ�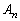 ��T�����Ƃɂ��܂��B�܂�A
��T�����Ƃɂ��܂��B�܂�A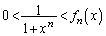 �ƂȂ�
�ƂȂ� �Őϕ��v�Z���ȒP�ɍs����`���l���܂��B
�Őϕ��v�Z���ȒP�ɍs����`���l���܂��B
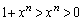 �Ȃ̂ŁA
�Ȃ̂ŁA �ł��B����āA
�ł��B����āA 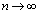 �̂Ƃ��A
�̂Ƃ��A �@����@
�@����@���ɁA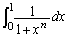 �ł����A
�ł����A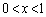 �̂Ƃ�
�̂Ƃ�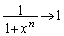 �Ȃ̂ŁA
�Ȃ̂ŁA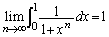 �ƂȂ肻���ł��B�����ŁA
�ƂȂ肻���ł��B�����ŁA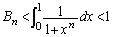 �C
�C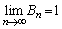 �ƂȂ�
�ƂȂ�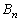 ��T�����ƂɂȂ�܂��B�܂�A
��T�����ƂɂȂ�܂��B�܂�A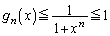 �ƂȂ�
�ƂȂ�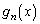 �Őϕ��v�Z���ȒP�ɍs����`���l���܂��B�����ŁA
�Őϕ��v�Z���ȒP�ɍs����`���l���܂��B�����ŁA �ł����A �Ȃ̂ŁA
�Ȃ̂ŁA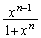 �ł���Ηe�Ղɐϕ��ł��܂��B
�ł���Ηe�Ղɐϕ��ł��܂��B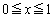 �ɂ����āA
�ɂ����āA ���A
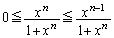 �C
�C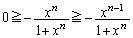
��  ����āA
����āA  �̂Ƃ��A
�̂Ƃ��A����āA�͂��݂����̌������A
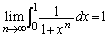 �@����A
�@����A�@�C�A���A
 ......[��]
......[��]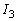 ���v�Z���Ă݂܂��B
���v�Z���Ă݂܂��B
�Ƃ����āA�E�ӂ�ʕ�����ƁA
��  �C
�C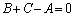 �C
�C
�� 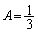 �C
�C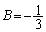 �C
�C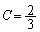
�� 
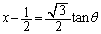 �Ƃ����ƁA
�Ƃ����ƁA
x�F �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F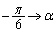 �C�������A
�C�������A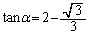
�ȏ���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B