چم‘ه—Œnگ”ٹw'09”N‘Oٹْ[4]
•½–تڈم‚جژOٹpŒ`OAB‚ًچl‚¦پA•سAB‚ج’†“_‚ًM‚ئ‚·‚éپB
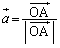 پC
پC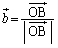
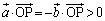 ‚إ‚ ‚é‚و‚¤‚ة‚ئ‚éپB’¼گüOP‚ةA‚©‚ç‰؛‚낵‚½گ‚گü‚ئ’¼گüOP‚جŒً“_‚ًQ‚ئ‚·‚éپB
‚إ‚ ‚é‚و‚¤‚ة‚ئ‚éپB’¼گüOP‚ةA‚©‚ç‰؛‚낵‚½گ‚گü‚ئ’¼گüOP‚جŒً“_‚ًQ‚ئ‚·‚éپB
(1) 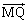 ‚ئ
‚ئ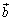 ‚ح•½چs‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
‚ح•½چs‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
(2) 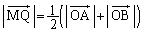 ‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
‚إ‚ ‚邱‚ئ‚ًژ¦‚¹پB
پyچLچگپz‚±‚±‚©‚çچLچگ‚إ‚·پB‚²——‚جٹF‚³‚ـ‚ج‚²ژx‰‡‚²—‰ً‚ًژ’‚肽‚پA‚و‚낵‚‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·پB
پyچLچگپzچLچگ‚ح‚±‚±‚ـ‚إ‚إ‚·پB
‰ً“ڑپ@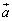 پC
پC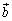 ‚ح’PˆتƒxƒNƒgƒ‹‚إ‚·پB
‚ح’PˆتƒxƒNƒgƒ‹‚إ‚·پB
‚؟‚ه‚ء‚ئŒ©‚½–ع‚إ‚ح•ûگj‚ً—§‚ؤ‚ة‚‚»‚¤‚إ‚·‚ھپA•½–تƒxƒNƒgƒ‹‚جٹî–{‚ة’‰ژہ‚ةپA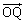 ‚ًپA
‚ًپA
‚ئپA1ژں“ئ—§‚ب2Œآ‚جƒxƒNƒgƒ‹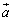 پC
پC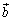 ‚ج1ژںŒ‹چ‡‚جŒ`‚ة•\‚·‚±‚ئ‚ة‚و‚è‰ًŒˆ‚إ‚«‚ـ‚·پB
‚ج1ژںŒ‹چ‡‚جŒ`‚ة•\‚·‚±‚ئ‚ة‚و‚è‰ًŒˆ‚إ‚«‚ـ‚·پB
Q‚ح’¼گüOPڈم‚ج“_‚ب‚ج‚إپAq‚ًژہگ”‚ئ‚µ‚ؤپA
‚ئ•\‚·‚±‚ئ‚ھ‚إ‚«‚ـ‚·پB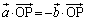 ‚و‚èپA
‚و‚èپA
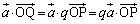
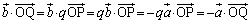 پ@¥¥¥‡@
پ@¥¥¥‡@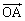 پC
پC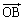 ‚ح1ژں“ئ—§پA‚آ‚ـ‚èپA
‚ح1ژں“ئ—§پA‚آ‚ـ‚èپA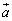 پC
پC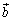 ‚ح1ژں“ئ—§‚ب‚ج‚إپAsپCt‚ًژہگ”‚ئ‚µ‚ؤپA
‚ح1ژں“ئ—§‚ب‚ج‚إپAsپCt‚ًژہگ”‚ئ‚µ‚ؤپA
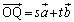 پ@¥¥¥‡A
پ@¥¥¥‡A
’چپD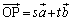 پC
پC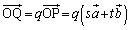 ‚ئ‚·‚é‚ج‚إ‚ح‰“‰ٌ‚è‚ة‚ب‚è‚ـ‚·پB“_P‚ة‚حˆس–،‚ھ‚ب‚¢‚±‚ئ‚ة’چˆس‚µ‚ؤ‚‚¾‚³‚¢پB
‚ئ‚·‚é‚ج‚إ‚ح‰“‰ٌ‚è‚ة‚ب‚è‚ـ‚·پB“_P‚ة‚حˆس–،‚ھ‚ب‚¢‚±‚ئ‚ة’چˆس‚µ‚ؤ‚‚¾‚³‚¢پB
‡@‚و‚èپA
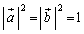 ‚و‚èپA
‚و‚èپA
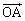 ‚ئ
‚ئ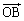 ‚ج‚ب‚·ٹp‚ًθ ‚ئ‚µ‚ؤ
‚ج‚ب‚·ٹp‚ًθ ‚ئ‚µ‚ؤ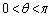 پC
پC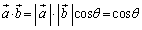 ‚و‚èپA
‚و‚èپA
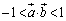 پ@¥¥¥‡B
پ@¥¥¥‡B
‚±‚ê‚و‚èپA
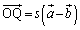 پ@¥¥¥‡C
پ@¥¥¥‡C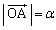 پC
پC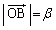 ‚ئ‚¨‚‚ئپA
‚ئ‚¨‚‚ئپA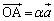 پC
پC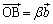 ‚ئ•\‚¹‚ـ‚·پB
‚ئ•\‚¹‚ـ‚·پB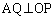 ‚و‚èپA
‚و‚èپA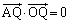 ‚إ‚·‚ھپA
‚إ‚·‚ھپA
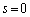 ‚ئ‚·‚é‚ئپA
‚ئ‚·‚é‚ئپA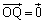 ‚ئ‚ب‚ء‚ؤ‚µ‚ـ‚¤‚ج‚إپA
‚ئ‚ب‚ء‚ؤ‚µ‚ـ‚¤‚ج‚إپA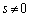 ‚إ‚·پB‚ـ‚½پA‡B‚و‚èپA
‚إ‚·پB‚ـ‚½پA‡B‚و‚èپA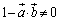
پˆ 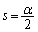
‡C‚و‚èپA
‚±‚ê‚و‚èپA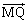 ‚ئ
‚ئ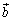 ‚ح•½چs‚إپA
‚ح•½چs‚إپA
‚±‚ê‚إپA(1)‚ئ(2)‚ھژ¦‚¹‚ـ‚µ‚½پB
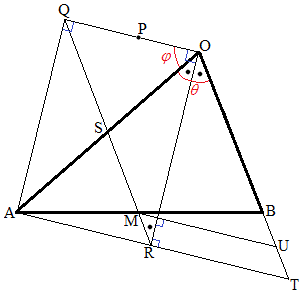 •ت‰ًپD•½–تٹô‰½‚إچl‚¦‚é•û‚ھ—eˆص‚©‚à’m‚ê‚ـ‚¹‚ٌپB
•ت‰ًپD•½–تٹô‰½‚إچl‚¦‚é•û‚ھ—eˆص‚©‚à’m‚ê‚ـ‚¹‚ٌپB
‚ب‚ج‚إپA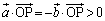 ‚ئ‚¢‚¤ڈًŒڈ‚و‚èپA
‚ئ‚¢‚¤ڈًŒڈ‚و‚èپA ‚و‚ء‚ؤپA
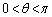 پC
پC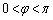 پC
پC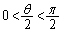 پC
پC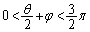 ‚و‚èپA
‚و‚èپA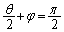
‚آ‚ـ‚èپA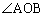 ‚ج“ٌ“™•ھگü‚ئ’¼گüOP‚حگ‚’¼‚إ‚·پB‘èˆس‚و‚èپA
‚ج“ٌ“™•ھگü‚ئ’¼گüOP‚حگ‚’¼‚إ‚·پB‘èˆس‚و‚èپA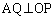 ‚ب‚ج‚إپAA‚ً’ت‚èOP‚ة•½چs‚ب’¼گü‚ئ
‚ب‚ج‚إپAA‚ً’ت‚èOP‚ة•½چs‚ب’¼گü‚ئ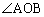 ‚ج“ٌ“™•ھگü‚ئ‚جŒً“_‚ًR‚ئ‚·‚é‚ئپAژlٹpŒ`OQAR‚ح’·•ûŒ`‚إ‚·پB
‚ج“ٌ“™•ھگü‚ئ‚جŒً“_‚ًR‚ئ‚·‚é‚ئپAژlٹpŒ`OQAR‚ح’·•ûŒ`‚إ‚·پB
’·•ûŒ`OQAR‚ج‘خٹpگüOA‚ئQR‚جŒً“_‚ًS‚ئ‚·‚é‚ئپAS‚حOAپCQR‚ج’†“_‚إپA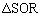 ‚ھ
‚ھ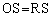 ‚إ‚ ‚é“ٌ“™•سژOٹpŒ`‚إ‚ ‚邱‚ئ‚©‚çپA
‚إ‚ ‚é“ٌ“™•سژOٹpŒ`‚إ‚ ‚邱‚ئ‚©‚çپAOR‚ھ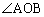 ‚ج“ٌ“™•ھگü‚إ‚ ‚邱‚ئ‚©‚çپA
‚ج“ٌ“™•ھگü‚إ‚ ‚邱‚ئ‚©‚çپA ‚و‚ء‚ؤپA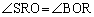 ‚و‚è
‚و‚è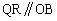
‚±‚ê‚و‚èپAQR‚حOA‚ج’†“_S‚ً’ت‚é‚ج‚إAB‚ج’†“_M‚à’ت‚è‚ـ‚·پB
پˆ 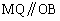 پˆ
پˆ 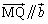
(2) A‚ً’ت‚èOP‚ة•½چs‚ب’¼گü‚ئ’¼گüOB‚ئ‚جŒً“_‚ًTپCM‚ً’ت‚èOP‚ة•½چs‚ب’¼گü‚ئ’¼گüOB‚ئ‚جŒً“_U‚ئ‚·‚é‚ئپAM‚حAB‚ج’†“_‚ب‚ج‚إپAU‚حBT‚ج’†“_‚إ‚·پB
OR‚ھ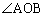 ‚ج“ٌ“™•ھگü‚إ‚ ‚邱‚ئ‚ئ
‚ج“ٌ“™•ھگü‚إ‚ ‚邱‚ئ‚ئ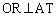 ‚إ‚ ‚邱‚ئ‚©‚çپA
‚إ‚ ‚邱‚ئ‚©‚çپA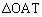 ‚ح
‚ح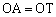 ‚إ‚ ‚é“ٌ“™•سژOٹpŒ`‚إ‚·پB
‚إ‚ ‚é“ٌ“™•سژOٹpŒ`‚إ‚·پB ‚ئپAژl•سŒ`OQMU‚ھ•½چsژl•سŒ`‚إ‚ ‚邱‚ئ‚©‚çپA
پyچLچگپz‚±‚±‚©‚çچLچگ‚إ‚·پB‚²——‚جٹF‚³‚ـ‚ج‚²ژx‰‡‚²—‰ً‚ًژ’‚肽‚پA‚و‚낵‚‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·پB
پyچLچگپzچLچگ‚ح‚±‚±‚ـ‚إ‚إ‚·پB
پ@پ@گ”ٹwTOPپ@پ@TOPƒyپ[ƒW‚ة–ك‚é
پyچLچگپz‚±‚±‚©‚çچLچگ‚إ‚·پB‚²——‚جٹF‚³‚ـ‚ج‚²ژx‰‡‚²—‰ً‚ًژ’‚肽‚پA‚و‚낵‚‚¨ٹè‚¢‚¢‚½‚µ‚ـ‚·پB
پyچLچگپzچLچگ‚ح‚±‚±‚ـ‚إ‚إ‚·پB
‹êٹwٹyٹwڈm گڈژ“ü‰ïژَ•t’†پI—Œn‘هٹwژَŒ±ƒlƒbƒgڈm‹êٹwٹyٹwڈm(‚²ˆؤ“à‚ح‚±‚؟‚ç)‚²“ü‰ï‚حپA
‚ـ‚¸پA‚±‚؟‚ç‚ـ‚إƒپپ[ƒ‹‚ً
‚¨‘—‚è‚‚¾‚³‚¢پB 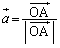 پC
پC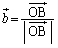
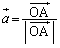 پC
پC