滋賀医大数学'09年[2]
(1) 積分 を
を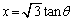 とおいて計算せよ。
とおいて計算せよ。 (2)  のとき、次の不等式を証明せよ。
のとき、次の不等式を証明せよ。 (3) nが2以上の自然数のとき、次の不等式を証明せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (3)は一見、区分求積法にも見えますが、
となるので、左辺カッコ内のの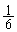 と
と をどう扱うかが問題になってしまいます。そこで、(2)を利用することを考えます。
をどう扱うかが問題になってしまいます。そこで、(2)を利用することを考えます。
(1) 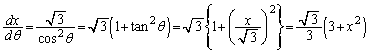 より、
より、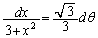
x: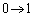 のときθ:
のときθ: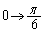
 (2)
(2) 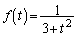 とすると、
とすると、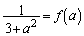 なので、証明すべき不等式の左辺は、
なので、証明すべき不等式の左辺は、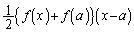 となり、
となり、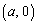 ,
,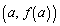 ,
,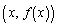 ,
, を4頂点とする台形(右図水色着色部分)の面積
を4頂点とする台形(右図水色着色部分)の面積 になっています。
になっています。右辺は、曲線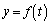 とt 軸、さらに、t 軸上の点
とt 軸、さらに、t 軸上の点 ,
,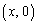 においてt 軸と垂直な2直線によって囲まれる部分の面積
においてt 軸と垂直な2直線によって囲まれる部分の面積 です。
です。 ここで、 の変化を調べてみます。
の変化を調べてみます。 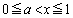 のとき、
のとき、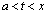 においては、
においては、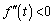 なので、
なので、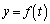 のグラフは上に凸です(曲線の凹凸を参照)。
のグラフは上に凸です(曲線の凹凸を参照)。
従って、曲線 のグラフは、
のグラフは、 において、2点
において、2点 ,
,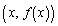 を結ぶ線分よりも上にきます。よって、
を結ぶ線分よりも上にきます。よって、∴  (証明終)
(証明終) (3) 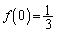 ,
,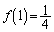 より、
より、
これと、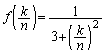 より、証明すべき不等式の左辺は、
より、証明すべき不等式の左辺は、 と変形できます。
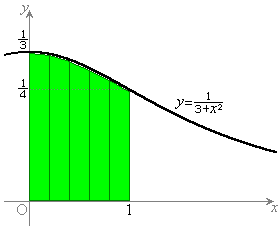
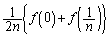 は、
は、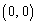 ,
,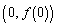 ,
, ,
,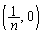 を4頂点とする台形の面積です。
を4頂点とする台形の面積です。
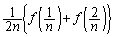 は、
は、 ,
, ,
,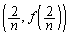 ,
, を4頂点とする台形の面積です。
を4頂点とする台形の面積です。
・・・・・・
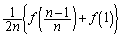 は、
は、 ,
,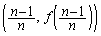 ,
, ,
,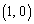 を4頂点とする台形の面積です。
を4頂点とする台形の面積です。
 の場合には、証明すべき不等式の左辺は、右図黄緑色着色部分の面積になります。
の場合には、証明すべき不等式の左辺は、右図黄緑色着色部分の面積になります。
 のとき、(2)において
のとき、(2)において ,
, とすると、
とすると、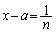 より、
より、
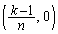 ,
,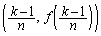 ,
, ,
,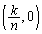 を4頂点とする台形の面積
を4頂点とする台形の面積 について、
について、 この不等式を、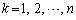 について辺々加え合わせることにより、
について辺々加え合わせることにより、 ∴  (証明終)
(証明終)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 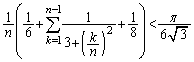
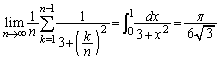
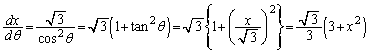 より、
より、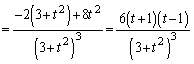
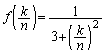 より、証明すべき不等式の左辺は、
より、証明すべき不等式の左辺は、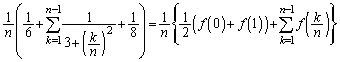
 (証明終)
(証明終)