�M�B��H���w'09�N[2]
����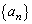 �ɂ�����
�ɂ�����
�Ƃ����B
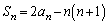 �@(
�@(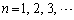 )
)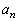 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����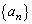 ��n���̘a
��n���̘a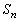 �Ɋւ��铙�����^�����Ă�����ł́A
�Ɋւ��铙�����^�����Ă�����ł́A
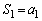 ��
��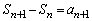 �𗘗p���܂�(����̘a�ƈ�ʍ����Q��)�B
�𗘗p���܂�(����̘a�ƈ�ʍ����Q��)�B
�܂��A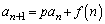 �Ƃ����`���Q�����́A
�Ƃ����`���Q�����́A
�E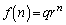 �ł���A
�ł���A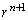 �Ŋ��邱�Ƃɂ��A
�Ŋ��邱�Ƃɂ��A �E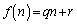 �ł���A
�ł���A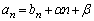 �Ƃ����đQ�����ɑ�����A
�Ƃ����đQ�����ɑ�����A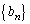 ������p�����䐔���ɂȂ�悤��α�Cβ ���߂邱�Ƃɂ��A��ʍ�
������p�����䐔���ɂȂ�悤��α�Cβ ���߂邱�Ƃɂ��A��ʍ�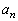 �����߂邱�Ƃ��ł��܂��B�{��͂��̃^�C�v�ł��B
�����߂邱�Ƃ��ł��܂��B�{��͂��̃^�C�v�ł��B �E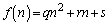 �ł���A
�ł���A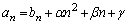 �Ƃ����đQ�����ɑ�����A
�Ƃ����đQ�����ɑ�����A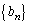 ������p�̓��䐔��ƂȂ�悤��α�Cβ�Cγ���߂邱�Ƃɂ��A��ʍ�
������p�̓��䐔��ƂȂ�悤��α�Cβ�Cγ���߂邱�Ƃɂ��A��ʍ�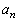 �����߂邱�Ƃ��ł��܂��B
�����߂邱�Ƃ��ł��܂��B
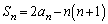 �@����@
�@����@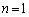 �Ƃ���ƁA
�Ƃ���ƁA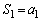 ���A
���A
�� 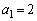 �@����A
�@����A
�@�ɂ����āAn��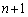 �ɑウ�āA
�ɑウ�āA
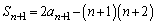 �@����B
�@����B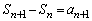 ���A
���A
�� 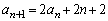 �@����C
�@����C
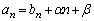 �@����D�@�Ƃ����đ������ƁA
�@����D�@�Ƃ����đ������ƁA
���D���̂Ƃ��A���ꂮ����A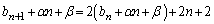 �Ƃ��Ȃ��悤�ɒ��ӂ��Ă��������B
�Ƃ��Ȃ��悤�ɒ��ӂ��Ă��������B
�������āA
�����ŁA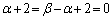 �C�܂�A
�C�܂�A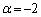 �C
�C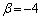 �̂Ƃ��A
�̂Ƃ��A
�ƂȂ�A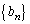 �͌���2�̓��䐔��ɂȂ�܂��B
�͌���2�̓��䐔��ɂȂ�܂��B
�D��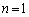 �Ƃ���ƁA�A���A
�Ƃ���ƁA�A���A
�� 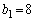
����āA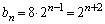
�D���A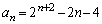 ......[��]
......[��]
�ʉ��D�C�ŁAn��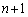 �ɑウ�āA
�ɑウ�āA
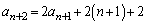 �@����E
�@����E
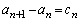 �Ƃ����ƁA
�Ƃ����ƁA
�F�|�G���A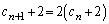
�C��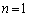 �Ƃ��āA
�Ƃ��āA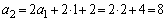
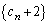 �́A�����F
�́A�����F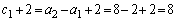 �C����2�̓��䐔��B
�C����2�̓��䐔��B
�� 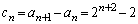
����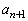 �ɇC�������āA
�ɇC�������āA
�� 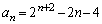 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B