���k�嗝�n���w'09�N�O��[6]
����a�ɑ��āAx�̕�����
���A���قȂ�4�̎����������悤��a�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ł͂���܂��A�n���Ŗʓ|�ȍl�@��K�v�Ƃ�����ł��B�����������ł����A���k��w��ڎw���C�����̋����������ƌ����邩���m��܂���B
�ȉ��ł́A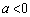 �̏ꍇ�̓O���t���王�o�I�ɔ��f�ł��܂����A
�̏ꍇ�̓O���t���王�o�I�ɔ��f�ł��܂����A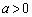 �̏ꍇ�͔��ʎ��Ȃǂׂ�K�v������܂��B
�̏ꍇ�͔��ʎ��Ȃǂׂ�K�v������܂��B
�Ȃ��A2�����A2���������̈�ʘ_�A2���������̉��̔z�u���Q�Ƃ��Ă��������B
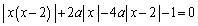 �@����@
�@����@
��Βl�L���̓����́A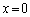 �ŕ������ς��Ƃ����
�ŕ������ς��Ƃ����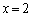 �ŕ������ς��Ƃ��낪���ꂼ��2�J�����邱�Ƃɖڂ����āA�@���A
�ŕ������ς��Ƃ��낪���ꂼ��2�J�����邱�Ƃɖڂ����āA�@���A
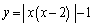 �@����A
�@����A
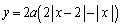 �@����B
�@����B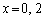 �ɂ����Đ�Βl�L���̓�����������ς��܂��B
�ɂ����Đ�Βl�L���̓�����������ς��܂��B
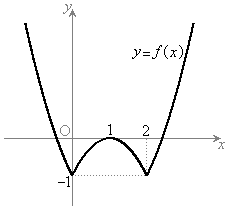 �A�́A
�A�́A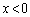 �C
�C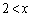 �̂Ƃ��A
�̂Ƃ��A
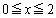 �̂Ƃ��A
�̂Ƃ��A
����āA�A�̃O���t�͉E�}�̂悤�ɂȂ�܂��B
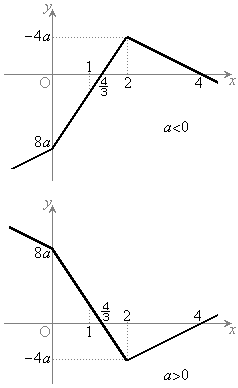 �B�́A
�B�́A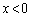 �̂Ƃ��A
�̂Ƃ��A
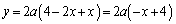 �@����C
�@����C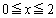 �̂Ƃ��A
�̂Ƃ��A
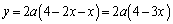 �@����D
�@����D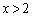 �̂Ƃ��A
�̂Ƃ��A
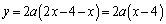 �@����E
�@����E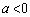 �C
�C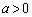 �̂Ƃ��A�E�}�̂悤�ɂȂ�܂�(
�̂Ƃ��A�E�}�̂悤�ɂȂ�܂�(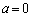 �̂Ƃ��͇B��x���Ɉ�v)�B���̂Ƃ��Aa�������Ȃ�l�ł����Ă��A
�̂Ƃ��͇B��x���Ɉ�v)�B���̂Ƃ��Aa�������Ȃ�l�ł����Ă��A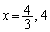 �̂Ƃ�
�̂Ƃ�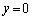 �ƂȂ邱�Ƃɒ��ӂ��܂��B�܂�A�B�̃O���t��a�̒l�ɂ�����炸�A�_
�ƂȂ邱�Ƃɒ��ӂ��܂��B�܂�A�B�̃O���t��a�̒l�ɂ�����炸�A�_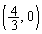 �C�_
�C�_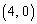 ��ʂ�܂��B
��ʂ�܂��B
�܂��A�B�́A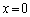 �̂Ƃ�
�̂Ƃ�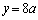 �C
�C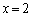 �̂Ƃ�
�̂Ƃ�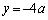 �ƂȂ�̂ŁA�_
�ƂȂ�̂ŁA�_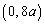 �C�_
�C�_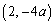 ��ʂ�܂�(����2�_�Ő܂�Ȃ���܂�)�B
��ʂ�܂�(����2�_�Ő܂�Ȃ���܂�)�B
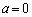 �̂Ƃ��B��x���Ɉ�v���܂����A�A��x���Ƒ��قȂ�3�̋��L�_�����̂ŁA�s�K�ł��B�Ȍ�A�A�̉E�ӂ�
�̂Ƃ��B��x���Ɉ�v���܂����A�A��x���Ƒ��قȂ�3�̋��L�_�����̂ŁA�s�K�ł��B�Ȍ�A�A�̉E�ӂ�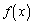 �Ƃ�����(
�Ƃ�����(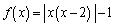 )�A
)�A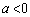 �C
�C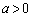 �̏ꍇ�ɕ����čl���܂��B
�̏ꍇ�ɕ����čl���܂��B
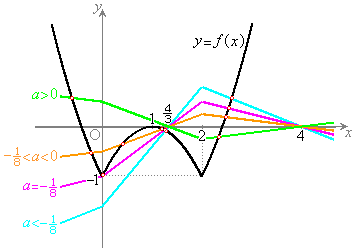 (i)
(i) 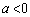 �̂Ƃ�
�̂Ƃ�(a) 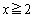 �ɂ����āA�B�́A
�ɂ����āA�B�́A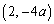 ��ʂ�A�E���X��
��ʂ�A�E���X��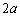 (
(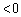 )�̒����̈ꕔ�ɂȂ�܂����A
)�̒����̈ꕔ�ɂȂ�܂����A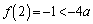 �C
�C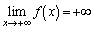 �ŁA
�ŁA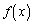 �͑����Ȃ̂ŁA
�͑����Ȃ̂ŁA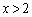 �ɂ����āA�A�ƇB�̃O���t��1��_�������A�������@��1���������܂��B
�ɂ����āA�A�ƇB�̃O���t��1��_�������A�������@��1���������܂��B (b) 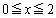 �ɂ����āA�B�́A
�ɂ����āA�B�́A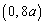 �C
�C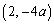 �𗼒[�Ƃ���X��
�𗼒[�Ƃ���X��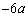 (
(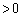 )�̐����ŁA
)�̐����ŁA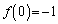 �ł���A
�ł���A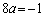 �C�܂�A
�C�܂�A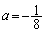 �̂Ƃ��A�_
�̂Ƃ��A�_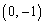 (�A�̃O���t��y���Ƃ̌�_)��ʂ�܂��B�A�̃O���t�͂��͈̔͂ŏ�ɓʂȂ̂ŁA�B���_
(�A�̃O���t��y���Ƃ̌�_)��ʂ�܂��B�A�̃O���t�͂��͈̔͂ŏ�ɓʂȂ̂ŁA�B���_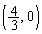 ��ʂ邱�Ƃ���A
��ʂ邱�Ƃ���A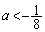 �ł���A���͈̔͂ɂ����āA�A�ƇB�̃O���t��1��_�������A�������@��1���������܂��B
�ł���A���͈̔͂ɂ����āA�A�ƇB�̃O���t��1��_�������A�������@��1���������܂��B 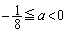 �̂Ƃ��A���͈̔͂ɂ����āA�A�ƇB�̃O���t��2�̋��L�_�������A�������@��2���������܂��B
�̂Ƃ��A���͈̔͂ɂ����āA�A�ƇB�̃O���t��2�̋��L�_�������A�������@��2���������܂��B(c) 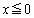 �ɂ����āA�B�́A
�ɂ����āA�B�́A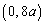 ��ʂ�A�X��
��ʂ�A�X��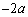 (
(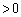 )�̐����ŁA
)�̐����ŁA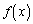 �͂��͈̔͂Ō����Ȃ̂ŁA
�͂��͈̔͂Ō����Ȃ̂ŁA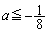 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A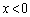 �ɂ����ćA�ƇB�͋��L�_���������A�������@�͉��������܂���B
�ɂ����ćA�ƇB�͋��L�_���������A�������@�͉��������܂���B 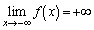 ���A
���A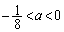 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A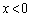 �ɂ����ćA�ƇB�͋��L�_��1�����A�������@��1���������܂��B
�ɂ����ćA�ƇB�͋��L�_��1�����A�������@��1���������܂��B�ȏ���A�������@��4�������̂́A
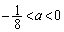 �@����F
�@����F(ii) 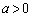 �̂Ƃ�
�̂Ƃ� 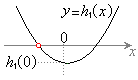 (a)
(a) 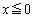 �ɂ����āA
�ɂ����āA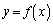 �ƇC��A������ƁA
�ƇC��A������ƁA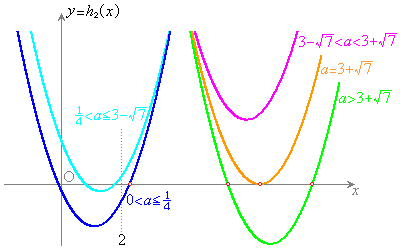 (b)
(b) 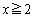 �ɂ����āA
�ɂ����āA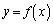 �ƇE��A������ƁA
�ƇE��A������ƁA���ʎ��F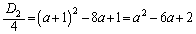
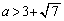 �̂Ƃ�
�̂Ƃ�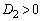 �Ȃ̂ŁA
�Ȃ̂ŁA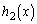 �̎��F
�̎��F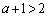 �C
�C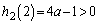 ���A
���A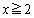 �ɂ����āA�A�ƇB�͌�_��2�����A�������@��2���������܂��B
�ɂ����āA�A�ƇB�͌�_��2�����A�������@��2���������܂��B
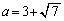 �̂Ƃ�
�̂Ƃ�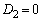 �ŁA
�ŁA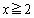 �ɂ����āA�������@��1��(�d��)�������܂��B
�ɂ����āA�������@��1��(�d��)�������܂��B
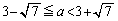 �̂Ƃ��A
�̂Ƃ��A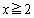 �ɂ����āA�������@�͉��������܂���B
�ɂ����āA�������@�͉��������܂���B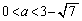 (
(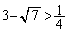 )�̂Ƃ��A
)�̂Ƃ��A �E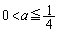 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A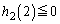 ���A
���A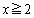 �ɂ����āA�������@��1���������܂��B
�ɂ����āA�������@��1���������܂��B 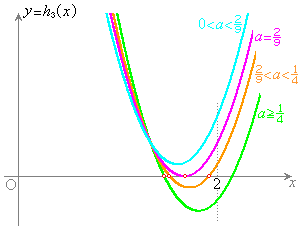 (c)
(c) 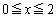 �ɂ����āA
�ɂ����āA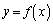 �ƇD��A������ƁA
�ƇD��A������ƁA���ʎ��F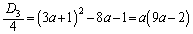
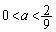 �̂Ƃ�
�̂Ƃ�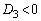 �Ȃ̂ŁA
�Ȃ̂ŁA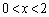 �ɂ����āA�������@�͉��������܂���B
�ɂ����āA�������@�͉��������܂���B
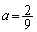 �̂Ƃ�
�̂Ƃ�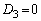 �ŁA
�ŁA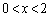 �ɂ����āA�������@��1��(�d��)
�ɂ����āA�������@��1��(�d��)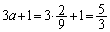 �������܂��B
�������܂��B
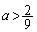 �̂Ƃ�
�̂Ƃ�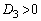 �ł����A
�ł����A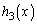 �̎��F
�̎��F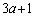 �C
�C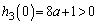 �C
�C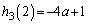 ���A
���A �E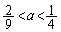 �̂Ƃ��ɂ́A���F
�̂Ƃ��ɂ́A���F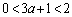 �C
�C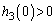 �C
�C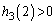 ���A
���A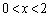 �ɂ����āA�������@��2���������܂��B
�ɂ����āA�������@��2���������܂��B �e�͈͂̉��̌��́Aa�̒l�ɏ]���Ĉȉ��̂悤�ɂȂ�܂��B�\���A�������@��4�����̂́A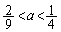 �C
�C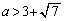 �@����G
�@����G �F�C�G���A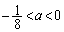 �C
�C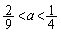 �C
�C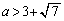 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B