徳島大数学'09年[4]
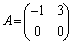 ,
,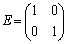 とする。
とする。
次の2つの等式を満たす2次の正方行列X,Yについて、下の問いに答えよ。
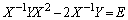 ,
,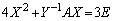
(1) 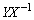 を求めよ。
を求めよ。 (2) Xを求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 最初から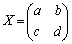 とおいてやっていくと大変なことになります。見通しが立つところまでは、Xのまま、行列の積が非可換(
とおいてやっていくと大変なことになります。見通しが立つところまでは、Xのまま、行列の積が非可換(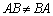 )であることに注意して文字式の計算を進めましょう。
)であることに注意して文字式の計算を進めましょう。
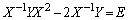 ・・・①
・・・①
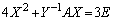 ・・・②
・・・②(1) 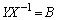 とおくと、右からXをかけて、
とおくと、右からXをかけて、 ③を①に代入すると、
左からX,右から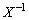 をかけて、
をかけて、 ∴ 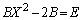 ・・・④
・・・④
∴ 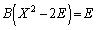 ・・・⑤
・・・⑤
②のままでは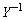 が面倒になるので、②両辺に左からYをかけて、
が面倒になるので、②両辺に左からYをかけて、 ③を代入して、
右から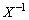 をかけて、
をかけて、 ④より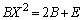 となるので、
となるので、 ∴ 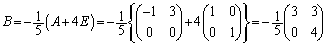 ∴
∴ 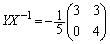 ......[答]
......[答]
(2) 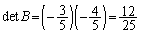 と、⑤より、
と、⑤より、 ∴ 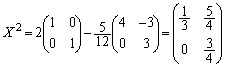
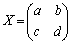 とおくと、
とおくと、 ⑦より、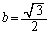
⑦より、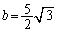
⑦より、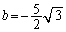
⑦より、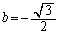
以上より、
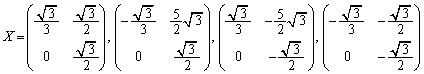 ......[答]
......[答]
別解.ハミルトン・ケーリーの定理より、
これを利用すると、Aの多項式はAの1次式で表せるので、以下のような解答も可能です。
の逆行列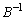 を、
を、
とおくと、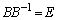 より、
より、
両辺を比較して、
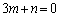 ,
,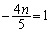
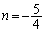 ,
,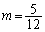
∴ 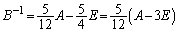
⑤より、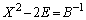 なので、
なので、
とおくと、
両辺を比較して、
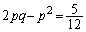 ,
,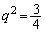
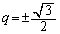
(i) 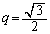 のとき、
のとき、 ∴ 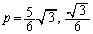 ∴
∴ 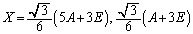
(ii) 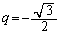 のとき、
のとき、 ∴ 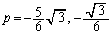 ∴
∴ 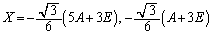
この問題ではかなり遠回りになりますが、一般的に使える解法です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
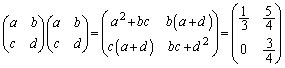
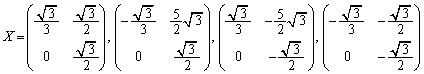 ......[答]
......[答]